tenzor je pole dat (čísla, funkce atd.), který je rozšířen v libovolném počtu (0 a větším) rozměrů. Počet dimenzí se nazývá hodnost tenzoru.

Rank 0 tenzor

tenzor, který nemá žádné rozměry (0).

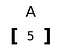
Rank 1 tenzor

tenzor, který je rozšířen pouze v jednom rozměru.

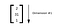
Rank 2 tensor

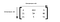
Rank 3 tensor

As shown in figure, a rank 3 tensor has a cube (or cuboid like structure).

If rank of a tensor exceeds 3, it becomes difficult to visualize.

Skalární

skalární je 0 hodnost tenzor. Ve fyzice jsou různá množství reprezentována jako skalár , jako jsou: Vzdálenost (500 km), teplota (10ºC), Rychlost (34 km/h) atd.

vektor

tenzor hodnosti 1 se nazývá vektor. Fyzikální veličiny, jako je rychlost (10 m / s), posun (54 m směrem na východ), elektromagnetické pole (1 V / m).

rozdíl mezi skalárem a vektorem :

veličina, která nevyžaduje další informace (například směr) s ní (jako teplota), je reprezentována jako skalární. Zatímco veličina, kterou je třeba specifikovat vedle její velikosti, je reprezentována vektorem (jako elektrické pole).

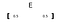
Vektor se značí s tučným písmenem (jako „E“ ) nebo šipkou nad písmenem.

pro vykreslení vektoru používáme jeho prvky jako hodnotu souřadnic (osa x, y a z). Zde je první prvek (0.5) považován za hodnotu x a druhý prvek (také 0.5) je považován za hodnotu y (kdybychom měli tři prvky, třetí by byla hodnota z).

Po vykreslení vektor jako bod jsme dát šipku na ni, od počátku(0,0).

vektor je jednoduše matice, která má buď jeden řádek (nazývaný sloupcový vektor) nebo jeden sloupec(nazývaný řádkový vektor).

matice

matice je tenzor řady 2. Podívali jsme se na matrix dříve.

tenzor s hodností větší než 2 se jednoduše nazývá „tenzor“ (neexistuje žádný specifický název pro tenzory s hodností vyšší než 2).

Pojem tenzor zobecňuje matice, vektory a skaláry pod jednou střechou (všechny jsou tenzory, ale s různých řad).

matice jako součin vektorů:

když se vynásobí dva vektory, vytvoří matici.

Vector X and Y combined, have 6 elements but their product alone has 9 elements. Některé matice by tedy mohly být rozděleny jako produkt dvou vektorů.