níže uvedený článek poskytuje bližší pohled na Cobb-douglasově Produkční Funkci.

funkce produkce Cobb-Douglas je založena na empirické studii amerického zpracovatelského průmyslu provedené Paulem h. Douglasem a C. W. Cobbem. Jedná se o lineární homogenní výrobní funkci prvního stupně, která bere v úvahu dva vstupy, práci a kapitál, pro celý výstup .výroba.

produkční funkce Cobb-Douglas je vyjádřena jako:

Q = ALa Cß

, kde Q je výstup a L a С jsou vstupy práce a kapitálu, resp. A, a a β jsou kladné parametry, kde = a > O, β > O

tato rovnice říká, že výkon přímo závisí na L a C, a část výstupu, která nemůže být vysvětlena tím, že L a С je vysvětlen, což je „zbytkové“, často volal technické změny.

produkční funkce řešen pomocí Cobb-Douglas měl 1/4 příspěvek kapitálu k růstu ve zpracovatelském průmyslu a 3/4 z práce tak, že je C-D produkční funkce je

Q = AL3/4 C1/4

, která vykazuje konstantní výnosy z rozsahu, protože součet hodnot L a С se rovná jedné: (3/4 + 1/4), tj.(a + β = 1) . Koeficient dělníka ve funkci C-D měří procentní nárůst v (Q, který by byl výsledkem 1% zvýšení v L, zatímco drží С jako konstantní.

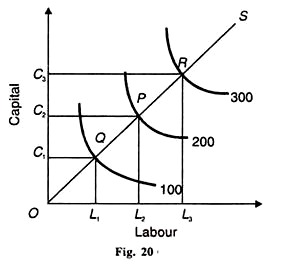
podobně, В je procentní nárůst Q, který by byl výsledkem 1% zvýšení C, zatímco drží L jako konstantní. Funkce produkce C-D ukazující konstantní návraty na stupnici je znázorněna na obrázku 20. Vstup práce se provádí na vodorovné ose a kapitál na svislé ose.

k výrobě 100 jednotek produkce se používají ОС, jednotky kapitálu a ol jednotky práce. Pokud by se produkce zdvojnásobila na 200, musely by se zdvojnásobit vstupy práce a kapitálu. ОС je přesně dvojnásobek ос1 a OL2 je dvojnásobek OL2.

Podobně, pokud má být zvýšena trojnásobně na 300 jednotek práce a kapitálu, bude muset být zvýšena na trojnásobek. OC3 a OL3 jsou třikrát větší než ОС1 a OL1. Další metodou je vzít linii stupnice nebo expanzní cestu spojující rovnovážné body Q, P A R. OS je čára stupnice nebo expanzní cesta spojující tyto body.

ukazuje, že izokvanty 100, 200 a 300 jsou stejně vzdálené. Na OS měřítku tedy oq = QP = PR ukazuje, že když se kapitál a práce zvyšují ve stejném poměru, výstup se také zvyšuje ve stejném poměru.

Kritika C-D Produkční Funkce:

C-D produkční funkce kritizovali, Šipky, Cheneryová, Minhas a Solow jak je uvedeno níže:

1. Výrobní funkce C-D zohledňuje pouze dva vstupy, práci a kapitál, a zanedbává některé důležité vstupy, jako jsou suroviny, které se používají ve výrobě. Není proto možné tuto funkci zobecnit na více než dva vstupy.

2. Ve výrobní funkci C-D vzniká problém měření kapitálu, protože vyžaduje pouze množství kapitálu dostupného pro výrobu. Plné využití dostupného kapitálu však lze provést pouze v období plné zaměstnanosti. To je nereálné, protože žádná ekonomika není vždy plně zaměstnána.

3. Funkce produkce C-D je kritizována, protože vykazuje konstantní návraty do měřítka. Konstantní návraty do měřítka však nejsou skutečností, protože na výrobu se vztahují buď rostoucí, nebo klesající výnosy do měřítka.

není možné měnit všechny vstupy, aby došlo k přiměřené změně výstupů všech průmyslových odvětví. Některé vstupy jsou vzácné a nelze je zvýšit ve stejném poměru jako bohaté vstupy. Na druhé straně vstupy jako stroje, podnikání atd. jsou nedělitelné. Vzhledem k tomu, že se produkce zvyšuje v důsledku použití nedělitelných faktorů na jejich maximální kapacitu, klesá cena za jednotku.

takže když je dodávka vstupů nedostatečná a jsou přítomny indivisibility, konstantní návrat do měřítka není možný. Kdykoli se ve výrobním procesu zvyšují jednotky různých vstupů, úspory z rozsahu a specializace vedou ke zvýšení výnosů z rozsahu.

v praxi však žádný podnikatel nebude chtít zvýšit různé jednotky vstupů, aby měl přiměřený nárůst produkce. Jeho snahou je více než přiměřený nárůst produkce, i když se nevylučuje ani klesající návratnost.

4. Funkce produkce C-D je založena na předpokladu nahraditelnosti faktorů a zanedbává komplementaritu faktorů.

5. Tato funkce je založena na předpokladu dokonalé konkurence na faktorovém trhu, který je nereálný. Pokud však tento předpoklad klesne, koeficienty α a β nepředstavují podíly faktorů.

6. Jednou ze slabin funkce C-D je problém agregace. Tento problém nastává, když je tato funkce aplikována na každou firmu v průmyslu a na celé odvětví. V této situaci bude mnoho výrobních funkcí nízké nebo vysoké agregace. Funkce C-D tedy neměří to, na co se zaměřuje.

závěr:

praktičnost výrobní funkce C-D ve zpracovatelském průmyslu je tedy pochybným návrhem. To se nevztahuje na zemědělství, kde při intenzivním pěstování nebude zvyšování množství vstupů zvyšovat produkci úměrně. Ani tehdy nelze popřít, že neustálé návraty do měřítka jsou etapou života firmy, průmyslu nebo ekonomiky. Další věc je, že tato fáze může přijít po nějaké době a na krátkou dobu.

je důležité:

navzdory těmto kritikám je funkce C-D velmi důležitá.

1. To bylo široce používáno v empirických studiích zpracovatelského průmyslu a v mezioborových srovnáních.

2. Používá se k určení relativních podílů práce a kapitálu na celkové produkci.

3. Používá se k prokázání Eulerovy věty.

4. Jeho parametry a A b představují koeficienty elasticity, které se používají pro meziodvětvová srovnání.

5. Tato produkční funkce lineárně homogenní stupně jedna, která vykazuje konstantní výnosy z rozsahu, je-Li α + β = 1, tam jsou rostoucí výnosy z rozsahu a je-li α + β < 1, existuje klesající výnosy z rozsahu.

6. Ekonomové rozšířili tuto výrobní funkci na více než dvě proměnné.