společný zápis funkce je obvykle psáno jako,

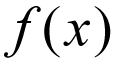
neberte to příliš doslovně, to znamená, že f je násoben x. Místo toho, zvažte to jako matematický výraz, který se čte jako

NEBO

Funkce může také být psán různými způsoby pomocí ostatních proměnných, jako jsou

• g(x), h(x), a k(x)

kromě toho, funkce může trvat další vstupní hodnoty jiné než x.

• f(a), h(r) a k(m)

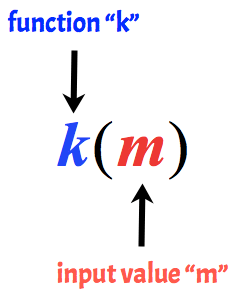
hlavní myšlenkou je, vždy si uvědomit, že proměnné mimo závorky je „jméno“ funkce, přičemž proměnné uvnitř závorek je vstupní hodnota funkce.

například, následující se nazývá funkce k s vstupní hodnotu m.

Základní Příklady Hodnocení Funkce

Příklad 1: Vyhodnocení funkce .

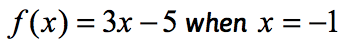
Toto je normální zápis funkce, kde je funkce f, zatímco vstupní hodnoty x. K vyhodnocení funkce, co chceme je nahradit každý výskyt x ve výrazu a pak zjednodušit.

OD x = – 1 nahradíme tuto hodnotu ve funkci a zjednodušíme. Přitom získáme řešení, které vypadá takto.

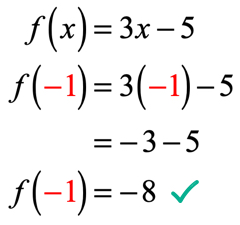
příklad 2: vyhodnoťte funkci .

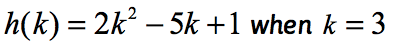
Pozorovat, že funkce zde je h a vstupní hodnota je k. Stejně jako v našem předchozím příkladu chceme nahradit jakoukoli číselnou hodnotu přiřazenou k do dané funkce a zjednodušit.

Vzhledem k = 3, vaše řešení by mělo vypadat podobně,

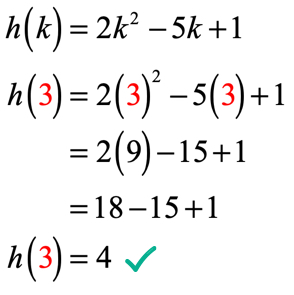
příklad 3: vyhodnoťte každou hodnotu x v tabulce níže pomocí níže uvedené funkce. Vykreslete body v ose xy a Spojte tečky, abyste odhalili graf funkce.

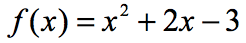
Protože je jich tam sedm x-vstupy, to znamená, že budeme hodnotit funkci sedmkrát stejně. Zkuste to vyřešit sami, pak se vraťte a zkontrolujte své odpovědi.

Pokud jste to udělali správně, jedná se o hodnoty:

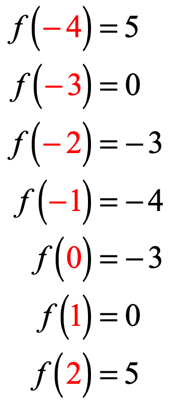
nyní můžeme tyto výstupní hodnoty umístit do tabulky.

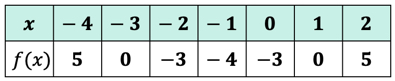
výstupní hodnoty funkce f\left( x \right) jako y-hodnoty. Takto vypadá graf na ose xy.

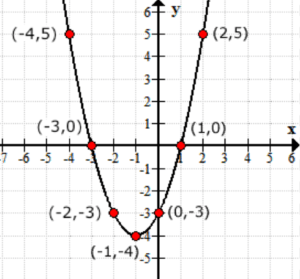
Intermediate Příklady Hodnocení Funkce

Příklad 4: Vzhledem k tomu, že g\left( x \right) = {x^2} – 3x + 1, najít g\left( {2x – 1} \right).

v předchozích příkladech jsme hodnotili funkci číslem. Tentokrát vstupní hodnota již není pevnou číselnou hodnotou, ale místo toho výrazem. Může to vypadat komplikovaně, ale postup zůstává stejný.

nahradíme každou instanci x v g\left (x \right) vstupní hodnotou, která je 2x-1. Zjednodušte tím, že umocníte binomický, použijete distribuční vlastnost a kombinujete podobné termíny.

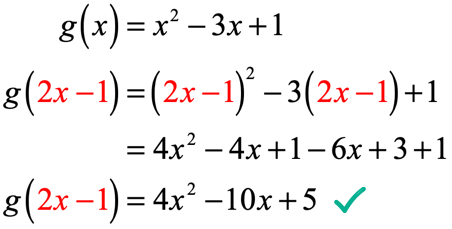
Příklad 5: Vzhledem k tomu, že p\left( x \right) = {{4x – 1} \over x} , vyhodnotit p\left( 1 \right) – p\left( { – 1} \right).

problém může zpočátku vypadat zastrašující, ale jakmile jej analyzujeme a použijeme to, co již víme, jak hodnotit funkce, nemělo by to být tak špatné!

zde musíme vyhodnotit funkci na x = 1 a poté odečíst hodnotu funkce při hodnocení na x = -\, 1.

buďte velmi opatrní při nahrazování hodnot a během procesu zjednodušení. Pokud si nejste opatrní v každém kroku, je velmi snadné se dopustit chyb, když sčítáte, odečítáte, násobíte nebo dělíte kladná a záporná čísla.

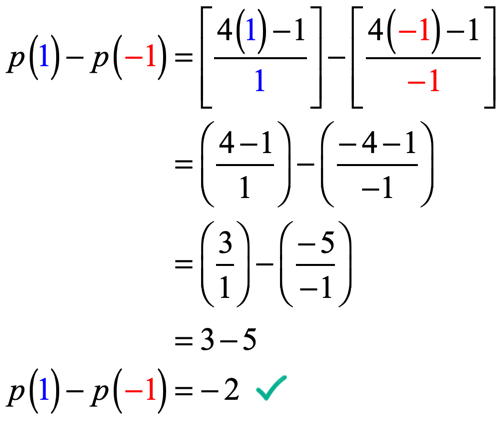
Pokročilé Příklad Použití Pojmu Hodnocení Funkce

Příklad 6: je-Li f\left( 2 \right) = 9, najít hodnotu ve funkci níže.

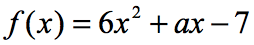
V rovnici, f\left( 2 \right) = 9, je nám řečeno, že pokud je vstup funkce je 2; výstup funkce bude 9. Vzhledem k tomu, že funkce je nám dána, naším prvním krokem je alespoň nahradit hodnotu 2 a poté zjednodušit. To je to, co dostaneme.

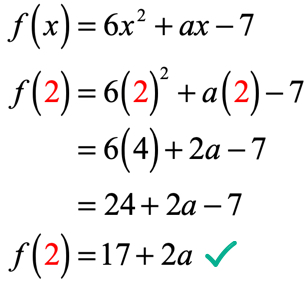
výstup z funkce po vyhodnocení v bodě x = 2 je 17 + 2a. Pamatujte si, my jsme také řekli, že výstup je 9 pomocí dané rovnice f\left( 2 \right) = 9. Proto to, co teď musíme udělat, je nastavit je navzájem rovné, a vyřešit lineární rovnici pro neznámou hodnotu.

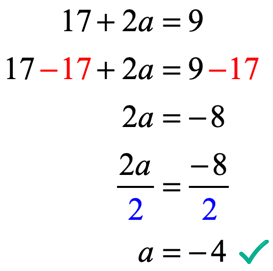
Pojďme si ověřit, zda na hodnotu a = – \,4 v f(x) = 6{x^2} + ax – 7 může daný stav f\left( 2 \right) = 9 být pravdivé prohlášení.

To je pravda! Proto jsme úspěšně vyřešili správnou hodnotu a.