alternativní normality test Shapiro-Wilk test.

• co je test Kolmogorov-Smirnov normality?
• SPSS Kolmogorov-Smirnov test z NPAR testů
• SPSS Kolmogorov-Smirnov test z zkoumat proměnné
• hlášení Kolmogorov-Smirnov Test
• nesprávné výsledky v SPSS?

Co je Kolmogorov-Smirnov normality test?

Kolmogorovův-Smirnovův test zkoumá, zda je pravděpodobné, že skóre
bude následovat v určité populaci.Pro zamezení nejasnostem, je tam 2 Kolmogorov-Smirnov testy:

• je zde jeden sample Kolmogorov-Smirnov test pro testování, pokud proměnná sleduje určité rozdělení v populaci. Toto „dané rozdělení“ je obvykle – ne vždy-normální rozdělení, proto „Kolmogorov-Smirnovův normálnost test“.
• existuje také (mnohem méně časté) nezávislé vzorky Kolmogorov-Smirnovův test pro testování, zda má proměnná identické distribuce ve 2 populacích.

V teorii, „Kolmogorov-Smirnov test“ může odkazovat se na jeden test (ale obvykle se odkazuje na jeden-sample Kolmogorov-Smirnov test) a bylo lepší se vyhnout. Mimochodem, oba testy Kolmogorov-Smirnov jsou přítomny v SPSS.

Kolmogorov-Smirnovův Test-jednoduchý příklad

takže řekněme, že mám populaci 1 000 000 lidí. Myslím, že jejich reakční doby na nějaký úkol jsou naprosto normálně rozloženy. I vzorek 233 z těchto lidí a měřit jejich reakční doby.
nyní se jejich pozorované frekvenční rozdělení bude pravděpodobně trochu lišit – ale ne příliš-od normálního rozdělení. Tak jsem běžel histogram přes pozorovat reakční časy a překrýt normální rozdělení se stejnou střední hodnotou a směrodatnou odchylku. Výsledek je uveden níže.

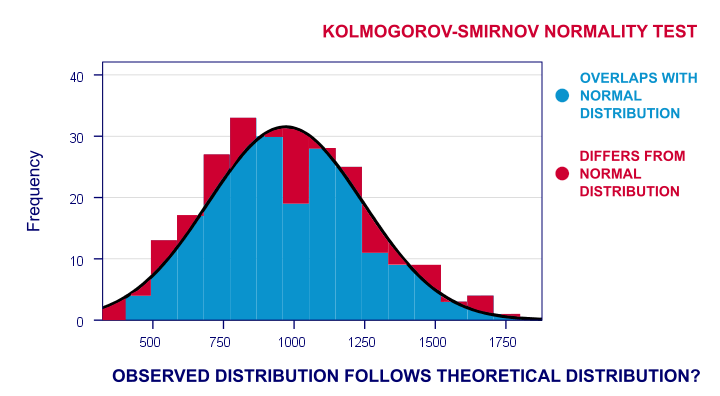
frekvenční distribuce mých skóre se zcela nepřekrývá s mou normální křivkou. Nyní bych mohl vypočítat procento případů, které se odchylují od normální křivky-procento červených oblastí v grafu. Toto procento je testovací statistika: vyjadřuje v jednom čísle, jak moc se moje data liší od mé nulové hypotézy. Ukazuje tedy, do jaké míry se pozorované skóre odchyluje od normálního rozdělení.
Pokud je moje nulová hypotéza pravdivá, pak by toto procento odchylky mělo být pravděpodobně poměrně malé. To znamená, že malá odchylka má vysokou hodnotu pravděpodobnosti nebo hodnotu p.
naopak, obrovské procento odchylek je velmi nepravděpodobné a naznačuje, že moje reakční doby nenásledují normální rozdělení v celé populaci. Takže velká odchylka má nízkou hodnotu p. Jako pravidlo, wereject nulovou hypotézu pokud p < 0.05.Takže pokud p < 0.05, nemůžeme uvěřit, že naše proměnná sleduje normální rozdělení v naší populaci.

Kolmogorov-Smirnov Test – Testovací Statistika

Takže to je nejjednodušší způsob, jak pochopit, jak Kolmogorov-Smirnov normality test funguje. Výpočetně to však funguje jinak: porovnává pozorované versus očekávané kumulativní relativní frekvence, jak je uvedeno níže.

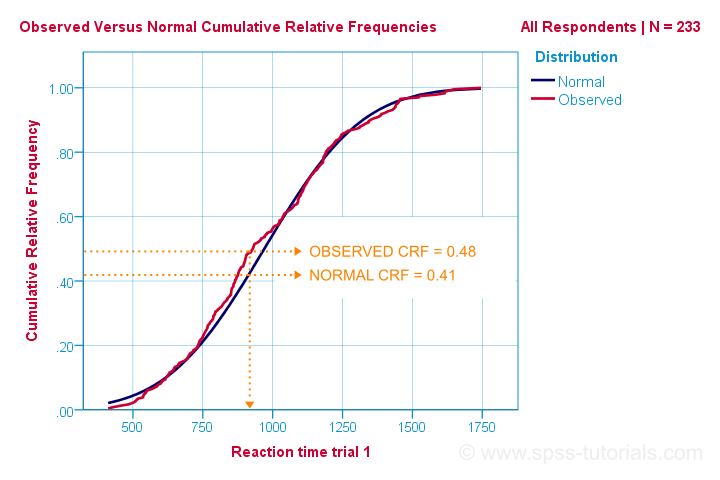
Kolmogorov-Smirnov test používá maximální absolutní rozdíl mezi těmito křivkami jako jeho testovací statistika označený D. V tomto grafu, maximální absolutní rozdíl D (0.48 – 0.41 =) 0,07 a to se vyskytuje v reakční dobou 960 milisekund. Mějte na paměti, že D = 0.07, jak se s ním setkáme v našem výstupu SPSS za minutu.

Kolmogorov-Smirnovův test v SPSS

existují 2 způsoby, jak spustit test v SPSS:

• TESTY NPAR, jak bylo zjištěno v rámci Analyzovat Neparametrické Testy Legacy Dialogs , 1-Sample K-S… je náš způsob volby, protože vytváří pěkně detailní výstup.
• prozkoumejte proměnné z analýzy Popisná statistika Prozkoumat je alternativou. Tento příkaz spouští jak test Kolmogorov-Smirnov, tak Test Shapiro-Wilk normality.
  všimněte si, že zkoumat proměnné používá listwise vyloučení chybějících hodnot ve výchozím nastavení. Takže pokud testuji 5 proměnných, mých 5 testů používá pouze případy, které nemají žádné chyby na žádné z těchto 5 proměnných. To obvykle není to, co chcete, ale ukážeme, jak se tomu vyhnout.

ukážeme obě metody pomocí speedtasks.sav v celém, jehož část je uvedena níže.

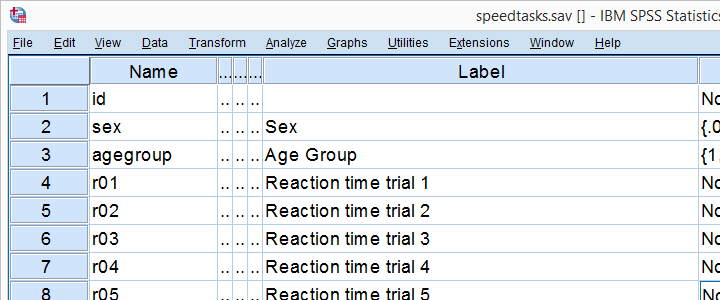
Naše hlavní výzkumná otázka iswhich reakční čas proměnných je pravděpodobně
běžně distribuován v naší populaci?Tato data jsou učebnicovým příkladem toho, proč byste měli svá data důkladně zkontrolovat, než je začnete upravovat nebo analyzovat. Udělejme to a spusťte některé histogramy ze syntaxe níže.

Výsledek

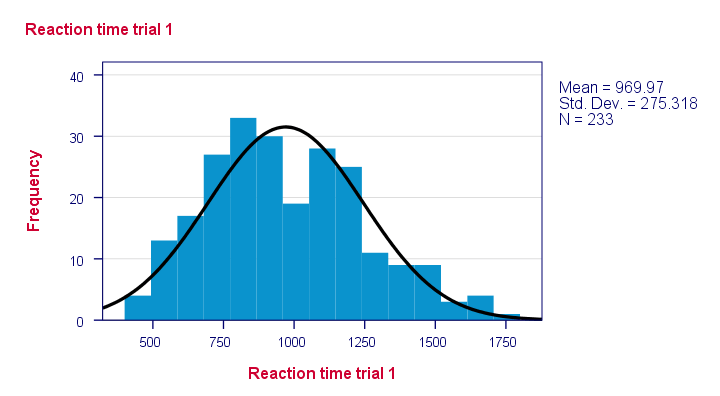
Všimněte si, že některé distribuce nemají vypadat věrohodně. Ale které z nich budou pravděpodobně normálně distribuovány?

SPSS Kolmogorov-Smirnov test z NPAR TESTS

Naše preferovaná volba pro běh Kolmogorov-Smirnov test je underAnalyze Neparametrické Testy Legacy Dialogs , 1-Sample K-S… jak je uvedeno níže.

dále jen vyplníme dialog, jak je uvedeno níže.

kliknutím na Vložit výsledky v syntaxi níže. Projedeme to.

Kolmogorov-Smirnov Test Syntaxe z Neparametrické Testy

Výsledky

za Prvé, na vědomí, že testovací statistika pro naše první proměnná dávce 0, 073 -stejně jako jsme viděli v naší kumulativní relativní četnost graf trochu dříve. Graf obsahuje přesně stejná data, na kterých jsme právě provedli náš test, takže tyto výsledky se pěkně sbíhají.
Pokud jde o naši výzkumnou otázku: pouze reakční doby pro pokus 4 se zdají být normálně distribuovány.

SPSS Kolmogorov-Smirnov test z ZKOUMAT PROMĚNNÉ

alternativní způsob, jak spustit Kolmogorov-Smirnov test začíná Analyzovat Popisné Statistiky Exploreas je uvedeno níže.

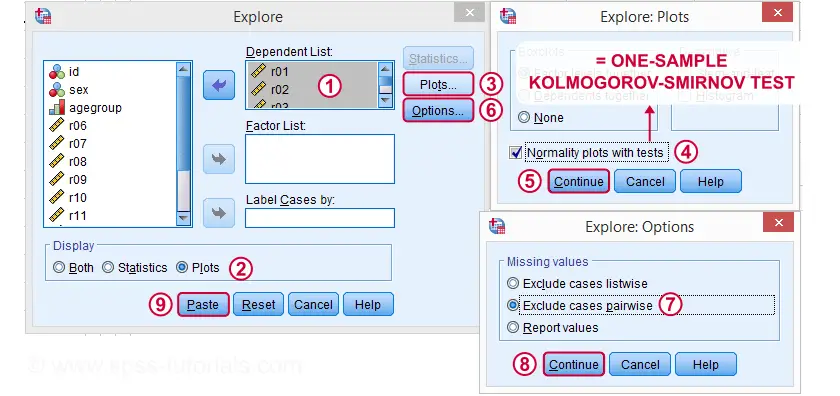
Kolmogorov-Smirnov Test Syntaxe z Neparametrické Testy

Results

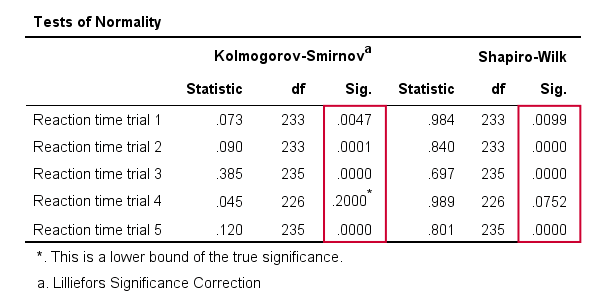
As a rule of thumb, we conclude thata variable is not normally distributed if „Sig.” < 0.05.Tak jak Kolmogorov-Smirnov test, stejně jako Shapiro-Wilk test výsledky naznačují, že pouze Reakce time trial 4 následuje normální distribuci v celé populaci.
dále si všimněte, že výsledky testu Kolmogorov-Smirnov jsou totožné s výsledky získanými z testů NPAR.

Hlášení Kolmogorov-Smirnov Test

Pro vykazování naše výsledky následující APA pokyny, budeme psát něco jako“Kolmogorov-Smirnov test ukazuje, že reakční časy na trial 1 nesledují normální rozdělení, D(233) = 0.07, p = 0.005.“Pro další proměnné, zkuste zkrátit to ale ujistěte se, že jsou

• D („rozdíl“), Kolmogorov-Smirnov test statistika,
• df stupňů volnosti (což je rovno N) a
• p, statistická významnost.

nesprávné výsledky v SPSS?

Pokud jste student, který chce jen složit test, můžete přestat číst. Postupujte podle kroků, o kterých jsme dosud diskutovali, a budete v pořádku.

správně, Nyní spusťte přesně stejné testy znovu v SPSS verze 18 a podívejte se na výstup.

V tomto výstupu, přesné p-hodnoty jsou zahrnuty a -naštěstí – jsou velmi blízko k asymptotická p-hodnoty. Méně naštěstí však výsledky SPSS verze 18 jsou divoce odlišné
od výsledků SPSS verze 24, které jsme dosud uváděli.
důvodem se zdá být korekce významnosti Lilliefors, která se používá v novějších verzích SPSS. Výsledkem se zdá být to, že význam asymptotické úrovně se liší mnohem více od přesný význam, než když oprava není samozřejmostí. To vyvolává vážné pochybnosti o správnosti výsledků „Lilliefors“ – výchozí v novějších verzích SPSS.
konvergující důkazy pro tento návrh shromáždil můj kolega Alwin Stegeman, který reran všechny testy v Matlabu. Výsledky Matlabu souhlasí s výsledky SPSS 18 a-tedy-ne s novějšími výsledky.

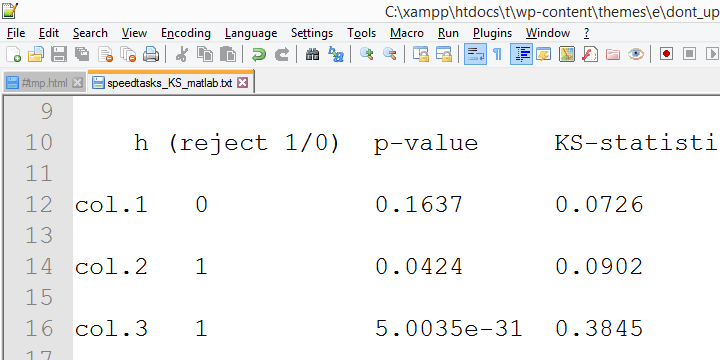
Kolmogorov-Smirnov normality test – Omezenou Užitečnost

Kolmogorov-Smirnov test je často k testování normality předpoklad vyžaduje mnoho statistických testů jako je ANOVA, t-test a mnoho dalších. Je však téměř běžně přehlíženo, že takové testy jsou robustní proti porušení tohoto předpokladu, pokud jsou velikosti vzorku přiměřené, řekněme n ≥ 25.Základním důvodem je centrální limitní věta. Proto jsou testy normality potřebné pouze pro malé velikosti vzorkupokud je cílem uspokojit předpoklad normality.
bohužel malé velikosti vzorků vedou k nízkému statistickému výkonu pro testy normality. To znamená, že podstatné odchylky od normality nebudou mít za následek statistickou významnost. Test říká, že neexistuje žádná odchylka od normality, zatímco je ve skutečnosti obrovská. Stručně řečeno, situace, ve které jsou potřebné testy normality-malé velikosti vzorků-je také situace, kdy fungují špatně.

Díky za přečtení.