Der unten genannte Artikel bietet einen genauen Überblick über die Cobb-Douglas-Produktionsfunktion. Die Cobb-Douglas-Produktionsfunktion basiert auf der empirischen Studie der amerikanischen Fertigungsindustrie von Paul H. Douglas und C.W. Cobb. Es ist eine lineare homogene Produktionsfunktion des Grades eins, die zwei Inputs, Arbeit und Kapital, für die gesamte Produktion des berücksichtigt.Fertigungsindustrie.

Die Cobb-Douglas-Produktionsfunktion wird ausgedrückt als:

Q = ALa Cß

wobei Q Output und L bzw. A, a und β sind positive Parameter where = a > O, β > O.

Die Gleichung besagt, dass die Ausgabe direkt von L und C abhängt, und der Teil der Ausgabe, der nicht durch L und C erklärt werden kann, wird durch A erklärt, was das „Residuum“ ist, das oft als technische Änderung bezeichnet wird.

Die von Cobb-Douglas gelöste Produktionsfunktion hatte 1/4 Beitrag des Kapitals zur Zunahme der verarbeitenden Industrie und 3/4 der Arbeit, so dass die CD-Produktionsfunktion ist

Q = AL3/ 4 C1/ 4

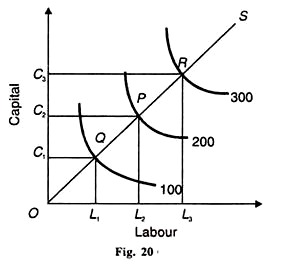
Dies zeigt konstante Skalenrenditen, da die Summe der Werte von L und D gleich eins ist: (3/4 + 1/4), d. H.(a + β = 1) . Der Koeffizient des Arbeiters in der C-D-Funktion misst den prozentualen Anstieg von (Q, der sich aus einem Anstieg von L um 1 Prozent ergeben würde, während er konstant bleibt. In ähnlicher Weise ist L der prozentuale Anstieg von Q, der sich aus einem Anstieg von C um 1 Prozent ergeben würde, während L konstant gehalten wird. Die C-D-Produktionsfunktion mit konstanten Skalenrückläufen ist in Abbildung 20 dargestellt. Der Arbeitseinsatz erfolgt auf der horizontalen Achse und das Kapital auf der vertikalen Achse.

Um 100 Produktionseinheiten zu produzieren, werden ОС, Kapitaleinheiten und OL-Arbeitseinheiten verwendet. Wenn die Produktion auf 200 verdoppelt werden sollte, müsste der Arbeits- und Kapitaleinsatz verdoppelt werden. ОС ist genau das Doppelte von ОС1 und von OL2 ist das Doppelte von OL2.

In ähnlicher Weise müssen die Einheiten von Arbeit und Kapital verdreifacht werden, wenn die Produktion auf 300 erhöht werden soll. OC3 und OL3 sind dreimal größer als ОС1 bzw. OL1. Eine andere Methode besteht darin, die Skalenlinie oder den Expansionspfad zu nehmen, die die Gleichgewichtspunkte Q, P und R verbinden.

Es zeigt, dass die Isoquanten 100, 200 und 300 äquidistant sind. Auf der OS-Skalenlinie OQ = QP = PR, die zeigt, dass, wenn Kapital und Arbeit in gleichen Anteilen erhöht werden, auch die Produktion in demselben Verhältnis zunimmt.

Kritik an der CD-Produktionsfunktion:

Die CD-Produktionsfunktion wurde von Arrow, Chenery, Minhas und Solow wie folgt kritisiert:

1. Die C-D-Produktionsfunktion berücksichtigt nur zwei Inputs, Arbeit und Kapital, und vernachlässigt einige wichtige Inputs wie Rohstoffe, die in der Produktion verwendet werden. Es ist daher nicht möglich, diese Funktion auf mehr als zwei Eingänge zu verallgemeinern.

2. In der C-D-Produktionsfunktion entsteht das Problem der Messung des Kapitals, weil es nur die für die Produktion verfügbare Kapitalmenge benötigt. Aber die volle Nutzung des verfügbaren Kapitals kann nur in Zeiten der Vollbeschäftigung erfolgen. Dies ist unrealistisch, da keine Volkswirtschaft immer vollbeschäftigt ist.

3. Die C-D-Produktionsfunktion wird kritisiert, weil sie konstante Skalenrenditen zeigt. Aber konstante Skalenrenditen sind keine Realität, denn entweder zunehmende oder abnehmende Skalenrenditen gelten für die Produktion.

Es ist nicht möglich, alle Inputs zu ändern, um eine proportionale Änderung der Outputs aller Branchen zu bewirken. Einige Inputs sind knapp und können nicht im gleichen Verhältnis wie reichlich vorhandene Inputs erhöht werden. Auf der anderen Seite Eingaben wie Maschinen, Unternehmertum usw. sind unteilbar. Wenn die Produktion aufgrund der Verwendung unteilbarer Faktoren auf ihre maximale Kapazität ansteigt, sinken die Kosten pro Einheit.

Wenn also das Angebot an Inputs knapp ist und Unteilbarkeiten vorhanden sind, sind konstante Skalenrenditen nicht möglich. Immer wenn die Einheiten verschiedener Inputs im Produktionsprozess erhöht werden, führen Skaleneffekte und Spezialisierung zu steigenden Skalenrenditen. In der Praxis wird jedoch kein Unternehmer die verschiedenen Inputeinheiten erhöhen wollen, um eine proportionale Steigerung der Produktion zu erzielen. Sein Bestreben ist es, die Produktion mehr als proportional zu steigern, auch wenn sinkende Skalenrenditen nicht ausgeschlossen sind.

4. Die C-D-Produktionsfunktion basiert auf der Annahme der Substituierbarkeit von Faktoren und vernachlässigt die Komplementarität von Faktoren.

5. Diese Funktion basiert auf der Annahme eines perfekten Wettbewerbs auf dem Faktormarkt, der unrealistisch ist. Wird diese Annahme jedoch verworfen, so stellen die Koeffizienten α und β keine Faktoranteile dar.

6. Eine der Schwächen der CD-Funktion ist das Aggregationsproblem. Dieses Problem tritt auf, wenn diese Funktion auf jedes Unternehmen in einer Branche und auf die gesamte Branche angewendet wird. In dieser Situation wird es viele Produktionsfunktionen mit niedriger oder hoher Aggregation geben. Daher misst die CD-Funktion nicht, was sie messen soll.

Schlussfolgerung:

Somit ist die Praktikabilität der C-D-Produktionsfunktion in der verarbeitenden Industrie eine zweifelhafte Aussage. Dies gilt nicht für die Landwirtschaft, in der bei intensivem Anbau eine Erhöhung der Inputmengen die Produktion nicht proportional erhöht. Selbst dann kann nicht geleugnet werden, dass konstante Skalenrenditen eine Etappe im Leben eines Unternehmens, einer Industrie oder einer Wirtschaft sind. Es ist eine andere Sache, dass diese Phase nach einiger Zeit und für kurze Zeit kommen kann.

Es ist wichtig:

Trotz dieser Kritik ist die CD-Funktion von großer Bedeutung.

1. Es wurde häufig in empirischen Studien der Fertigungsindustrie und in Branchenvergleichen verwendet.

2. Es wird verwendet, um die relativen Anteile von Arbeit und Kapital an der Gesamtproduktion zu bestimmen.

3. Es wird verwendet, um den Satz von Euler zu beweisen.

4. Seine Parameter a und b stellen Elastizitätskoeffizienten dar, die für sektorübergreifende Vergleiche verwendet werden.

5. Diese Produktionsfunktion ist linear homogen von Grad eins, der konstante Skalenrenditen zeigt, Wenn α + β = 1, gibt es zunehmende Skalenrenditen und wenn α + β < 1, gibt es abnehmende Skalenrenditen.

6. Ökonomen haben diese Produktionsfunktion auf mehr als zwei Variablen erweitert.