Die allgemeine Notation einer Funktion wird normalerweise wie folgt geschrieben:

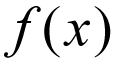
wörtlich, das heißt, f wird mit x multipliziert. Betrachten Sie dies stattdessen als mathematischen Ausdruck, der gelesen wird als

ODER

Funktionen können auch auf verschiedene Arten mit anderen Variablen geschrieben werden, z. B.

• g(x), h (x) und k(x)

Zusätzlich können Funktionen andere Eingabewerte als x.

• f(a), h(r) und k(m)

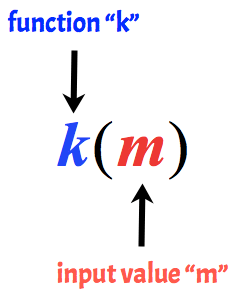
Die Schlüsselidee ist immer, sich daran zu erinnern, dass die Variable außerhalb der Klammer der „Name“ der Funktion ist, während die Variable innerhalb der Klammer der Eingabewert der Funktion ist.

Beispielsweise wird die Funktion k mit einem Eingabewert von m aufgerufen.

Grundlegende Beispiele für die Auswertung von Funktionen

Beispiel 1: Bewerten Sie die Funktion .

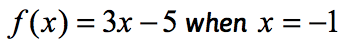
Dies ist die normale Notation der Funktion, bei der die Funktion f ist, während der Eingabewert x ist. Um eine Funktion auszuwerten, müssen wir jede Instanz von x im Ausdruck ersetzen und dann vereinfachen.

Da x = – 1 ist , ersetzen wir diesen Wert in der Funktion und vereinfachen. Auf diese Weise erhalten wir eine Lösung, die so aussieht.

Beispiel 2: Werten Sie die Funktion aus .

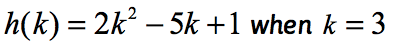
Beachten Sie, dass die Funktion hier h und der Eingabewert k ist. Genau wie in unserem vorherigen Beispiel möchten wir den k zugewiesenen numerischen Wert in die gegebene Funktion ersetzen und vereinfachen.

Da k = 3 ist, sollte Ihre Lösung ähnlich aussehen

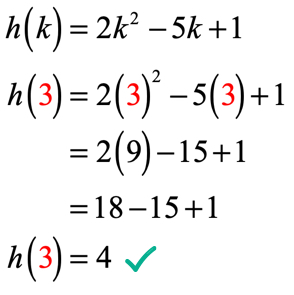
Beispiel 3: Werten Sie jeden Wert von x in der folgenden Tabelle mit der folgenden Funktion aus. Zeichnen Sie die Punkte in der xy-Achse und verbinden Sie die Punkte, um das Diagramm der Funktion anzuzeigen.

Da es sieben x-Eingänge gibt, bedeutet dies, dass wir die Funktion auch sieben Mal auswerten werden. Versuchen Sie, dies selbst herauszufinden, und kommen Sie dann zurück, um Ihre Antworten zu überprüfen.

Wenn Sie es richtig gemacht haben, sind dies die Werte:

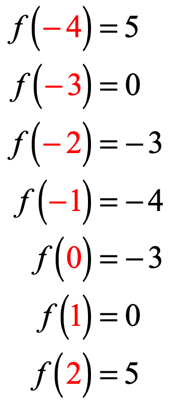
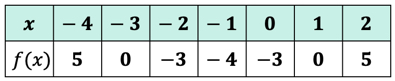
Wir können diese Ausgabewerte nun in die Tabelle einfügen.

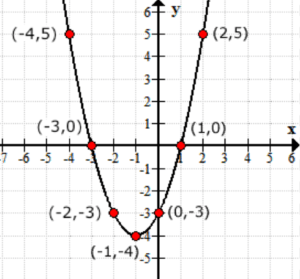
Stellen Sie sich die Ausgabewerte der Funktion f\left( x \right) als y-Werte vor. So sieht der Graph auf der xy-Achse aus.

Zwischenbeispiele für die Auswertung von Funktionen

Beispiel 4: Wenn g\left( x \right) = {x^2} – 3x + 1 , finden Sie g\left( {2x – 1} \right).

In früheren Beispielen haben wir eine Funktion anhand einer Zahl ausgewertet. Diesmal ist der Eingabewert kein fester numerischer Wert mehr, sondern ein Ausdruck. Es mag kompliziert aussehen, aber das Verfahren bleibt gleich.

Wir ersetzen jede Instanz von x in g\left( x \right) durch den Eingabewert 2x – 1 . Vereinfachen Sie, indem Sie das Binom quadrieren, die distributive Eigenschaft anwenden und ähnliche Terme kombinieren.

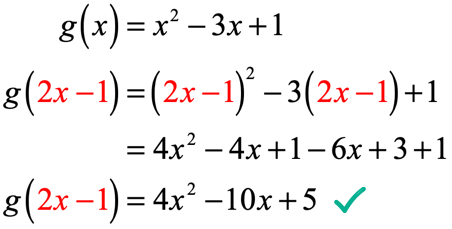
Beispiel 5: Wenn p\left( x \right) = {{4x – 1} \over x} , werten Sie p\left( 1 \right) – p\left( { – 1} \right) aus.

Das Problem mag zunächst einschüchternd aussehen, aber sobald wir es analysiert und das, was wir bereits wissen, auf die Bewertung von Funktionen angewendet haben, sollte dies nicht so schlimm sein!

Hier müssen wir die Funktion bei x = 1 auswerten und dann den Wert der Funktion subtrahieren, wenn sie bei x = – \,1 ausgewertet wird.

Seien Sie sehr vorsichtig, wenn Sie die Werte ersetzen und während des Vereinfachungsprozesses. Wenn Sie nicht in jedem Schritt vorsichtig sind, ist es sehr einfach, Fehler zu begehen, wenn Sie positive und negative Zahlen addieren, subtrahieren, multiplizieren oder dividieren.

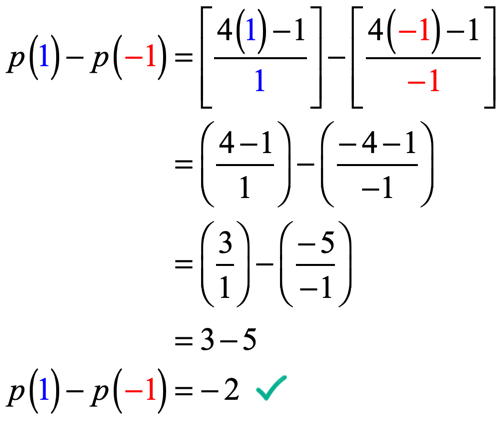
Erweitertes Beispiel für die Anwendung des Konzepts der Auswertung von Funktionen

Beispiel 6: Wenn f\left( 2 \right) = 9 , finden Sie den Wert von a in der folgenden Funktion.

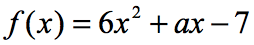
In der Gleichung, f\left( 2 \right) = 9, wird uns gesagt, dass, wenn die Eingabe der Funktion 2 ist; die Ausgabe der Funktion ist 9. Da uns die Funktion gegeben ist, besteht unser erster Schritt darin, mindestens den Wert 2 zu ersetzen und dann zu vereinfachen. Das bekommen wir.

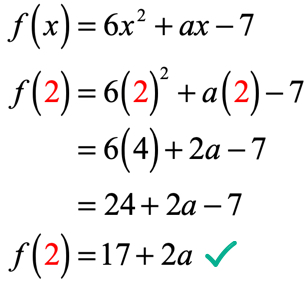
Die Ausgabe der Funktion nach der Auswertung bei x = 2 ist 17 + 2a. Denken Sie daran, dass uns auch gesagt wird, dass die Ausgabe 9 ist, indem die gegebene Gleichung f\left( 2 \right) = 9 verwendet wird. Deshalb müssen wir sie jetzt gleich setzen und die lineare Gleichung für den unbekannten Wert von a lösen.

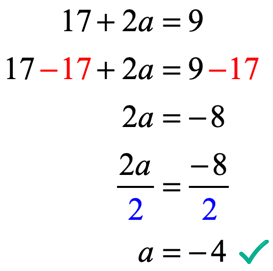
Überprüfen wir, ob der Wert von a = – \,4 in f(x) = 6{x^2} + ax – 7 die gegebene Bedingung f\left(2 \right) = 9 zu einer wahren Aussage machen kann.

Es ist wahr! Daher haben wir erfolgreich für den korrekten Wert von a gelöst.