Regressionsanalyse > Homoskedastizität / Homogenität der Varianz / Annahme gleicher Varianz

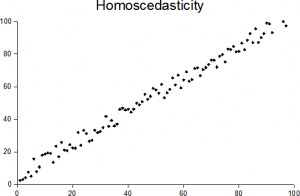
Bild: Sreebot | Wikimedia Commons

Einfach ausgedrückt bedeutet Homoskedastizität „die gleiche Streuung haben.“ Damit es in einem Datensatz vorhanden ist, müssen die Punkte ungefähr den gleichen Abstand von der Linie haben, wie im Bild oben gezeigt. Das Gegenteil ist die Heteroskedastizität („unterschiedliche Streuung“), bei der Punkte in stark unterschiedlichen Abständen von der Regressionsgeraden liegen.

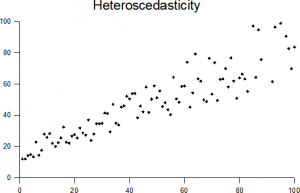
Die Punkte höher auf der x-Achse haben eine größere Varianz als kleinere Werte.

Beachten Sie, dass ich hier „Entfernung“ und nicht Varianz gesagt habe. Beim Anzeigen eines Diagramms ist es einfacher, die Abstände zwischen den Punkten und der Linie zu betrachten, um festzustellen, ob ein Datensatz Homoskedastizität aufweist. Technisch gesehen ist es die Varianz, die zählt, und das würden Sie in Berechnungen verwenden. Da die Varianz jedoch eine Formel erfordert, ist es unmöglich, einen Augapfel in einem Diagramm zu sehen.

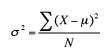
Varianzformel.

Da Varianz nur die Standardabweichung im Quadrat ist, können Sie Homoskedastizität auch als eine Bedingung beschreiben, bei der die Standardabweichungen für alle Punkte gleich sind.

Formeller ausgedrückt

Sie werden selten auf einen Datensatz stoßen, der eine Varianz von Null aufweist. Es ist wahrscheinlicher, dass Abweichungen zwischen 0,01 und 101,01 auftreten. Wann wird ein Datensatz als Homoskedastizität eingestuft? Die allgemeine Faustregel1 lautet:

Wenn das Verhältnis der größten zur kleinsten Varianz 1,5 oder weniger beträgt, sind die Daten homoskedastisch.

Was ist die Annahme gleicher Varianz?

Die Annahme gleicher Varianzen (d. h. Annahme der Homoskedastizität) geht davon aus, dass verschiedene Proben die gleiche Varianz haben, auch wenn sie aus verschiedenen Populationen stammen. Die Annahme findet sich in vielen statistischen Tests, einschließlich Varianzanalyse (ANOVA) und Student’s T-Test. Andere Tests, wie Welchs T-Test, erfordern überhaupt keine gleichen Varianzen.Wenn Sie einen Test ausführen, ohne auf gleiche Abweichungen zu prüfen, kann dies erhebliche Auswirkungen auf Ihre Ergebnisse haben und diese sogar vollständig ungültig machen. Wie stark Ihre Ergebnisse beeinflusst werden, hängt davon ab, welchen Test Sie verwenden und wie empfindlich dieser Test auf ungleiche Varianzen reagiert. Während beispielsweise ein ANOVA-Test mit festem Faktor und gleichen Stichprobenumfängen nur eine winzige Menge betrifft, kann eine ANOVA mit ungleichen Stichprobenumfängen zu völlig ungültigen Ergebnissen führen.

Die Annahme gleicher Varianzen wird auch in der linearen Regression verwendet, die davon ausgeht, dass Daten homoskedastisch sind. In einfachen Worten, wenn Ihre Daten weit verbreitet sind (wie die Kegelform im heteroskedastischen Bild oben), wird die Regression nicht so gut funktionieren. Weitere Informationen zu diesem Thema finden Sie unter Annahmen & Bedingungen für die Regression.

Testen auf Homogenität der Varianz

Zu den Tests, die Sie ausführen können, um zu überprüfen, ob Ihre Daten dieser Annahme entsprechen, gehören:

• Bartlett-Test
• Box-M-Test
• Brown-Forsythe-Test
• Hartleys Fmax-Test
• Levene-Test

——————————————————————————

Brauchen Sie Hilfe bei einer Hausaufgabe oder Testfrage? Mit Chegg Study erhalten Sie Schritt-für-Schritt-Lösungen für Ihre Fragen von einem Experten auf diesem Gebiet. Deine ersten 30 Minuten mit einem Chegg Tutor sind kostenlos!