Ein alternativer Normalitätstest ist der Shapiro-Wilk-Test.

• Was ist ein Kolmogorov-Smirnov-Normalitätstest?
• SPSS Kolmogorov-Smirnov-Test aus NPAR-TESTS
• SPSS Kolmogorov-Smirnov-Test aus VARIABLEN UNTERSUCHEN
• Einen Kolmogorov-Smirnov-Test melden
• Falsche Ergebnisse in SPSS?

Was ist ein Kolmogorov-Smirnov Normalitätstest?

Der Kolmogorov-Smirnov-Test untersucht, ob die Ergebnisse
wahrscheinlich einer Verteilung in einer Population folgen.Um Verwirrung zu vermeiden, gibt es 2 Kolmogorov-Smirnov-Tests:

• Es gibt den einen Beispiel-Kolmogorov-Smirnov-Test zum Testen, ob eine Variable einer bestimmten Verteilung in einer Population folgt. Diese „gegebene Verteilung“ ist normalerweise – nicht immer – die Normalverteilung, daher „Kolmogorov-Smirnov-Normalitätstest“.
• Es gibt auch den (viel weniger verbreiteten) unabhängigen Kolmogorov-Smirnov-Test, um zu testen, ob eine Variable in 2 Populationen identische Verteilungen aufweist.

Theoretisch könnte sich „Kolmogorov-Smirnov-Test“ auf einen der beiden Tests beziehen (bezieht sich jedoch normalerweise auf den Kolmogorov-Smirnov-Test mit einer Stichprobe) und sollte besser vermieden werden. Übrigens sind beide Kolmogorov-Smirnov-Tests in SPSS vorhanden.

Kolmogorov-Smirnov-Test – Einfaches Beispiel

Angenommen, ich habe eine Bevölkerung von 1.000.000 Menschen. Ich denke, ihre Reaktionszeiten bei einer Aufgabe sind vollkommen normal verteilt. Ich probiere 233 dieser Leute aus und messe ihre Reaktionszeiten.
Nun wird sich die beobachtete Häufigkeitsverteilung dieser wahrscheinlich ein wenig – aber nicht zu sehr – von einer Normalverteilung unterscheiden. Also führe ich ein Histogramm über die beobachteten Reaktionszeiten und überlagere eine Normalverteilung mit dem gleichen Mittelwert und der gleichen Standardabweichung. Das Ergebnis ist unten dargestellt.

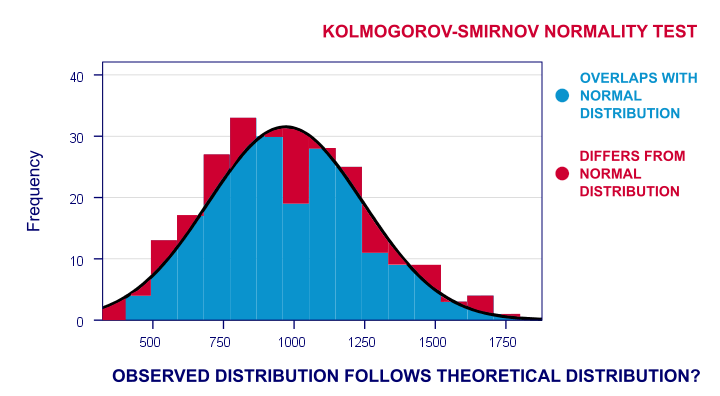
Die Häufigkeitsverteilung meiner Ergebnisse überschneidet sich nicht vollständig mit meiner normalen Kurve. Jetzt konnte ich den Prozentsatz der Fälle berechnen, die von der normalen Kurve abweichen – den Prozentsatz der roten Bereiche im Diagramm. Dieser Prozentsatz ist eine Teststatistik: Er drückt in einer einzigen Zahl aus, wie sehr sich meine Daten von meiner Nullhypothese unterscheiden. Es zeigt also an, inwieweit die beobachteten Werte von einer Normalverteilung abweichen.
Nun, wenn meine Nullhypothese wahr ist, dann sollte dieser Abweichungsprozentsatz wahrscheinlich ziemlich klein sein. Das heißt, eine kleine Abweichung hat einen hohen Wahrscheinlichkeitswert oder p-Wert.Umgekehrt ist ein großer Abweichungsprozentsatz sehr unwahrscheinlich und deutet darauf hin, dass meine Reaktionszeiten nicht einer Normalverteilung in der gesamten Population folgen. Eine große Abweichung hat also einen niedrigen p-Wert. Als Faustregel gilt die Nullhypothese, wenn p < 0.05.So wenn p < 0.05 , glauben wir nicht, dass unsere Variable einer Normalverteilung in unserer Population folgt.

Kolmogorov-Smirnov-Test – Teststatistik

Das ist also der einfachste Weg zu verstehen, wie der Kolmogorov-Smirnov-Normalitätstest funktioniert. Rechnerisch funktioniert es jedoch anders: Es vergleicht die beobachteten mit den erwarteten kumulativen relativen Häufigkeiten, wie unten gezeigt.

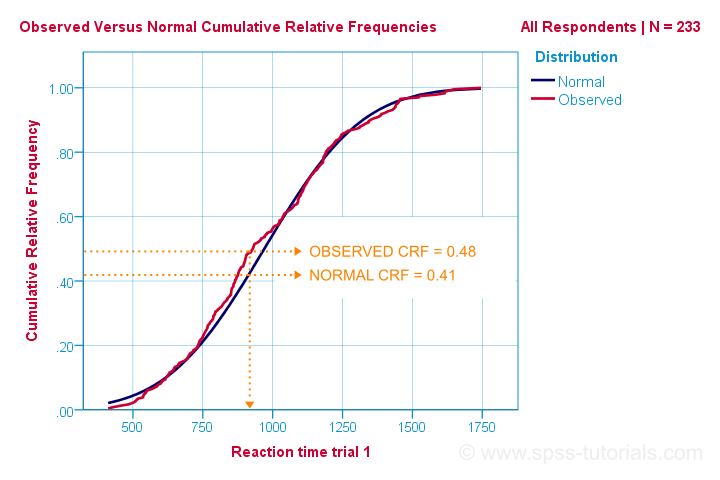
Der Kolmogorov-Smirnov-Test verwendet die maximale absolute Differenz zwischen diesen Kurven als Teststatistik, die mit D bezeichnet wird. In diesem Diagramm beträgt die maximale absolute Differenz D (0,48 – 0,41 =) 0,07 und tritt bei einer Reaktionszeit von 960 Millisekunden auf. Denken Sie daran, dass D = 0,07 ist, da wir es in einer Minute in unserer SPSS-Ausgabe finden werden.

Der Kolmogorov-Smirnov-Test in SPSS

Es gibt 2 Möglichkeiten, den Test in SPSS auszuführen:

• NPAR-TESTS wie unter Analysieren Nichtparametrische Tests Legacy-Dialoge 1-Beispiel K-S… ist unsere Methode der Wahl, weil es schön detaillierte Ausgabe erstellt.
• UNTERSUCHEN SIE VARIABLEN aus Analyze Descriptive Statistics Explore ist eine Alternative. Dieser Befehl führt sowohl den Kolmogorov-Smirnov-Test als auch den Shapiro-Wilk-Normalitätstest aus.
  Beachten Sie, dass EXAMINE VARIABLES standardmäßig den listenweisen Ausschluss fehlender Werte verwendet. Wenn ich also 5 Variablen teste, verwenden meine 5 Tests nur Fälle, in denen keine dieser 5 Variablen fehlt. Dies ist normalerweise nicht das, was Sie wollen, aber wir zeigen Ihnen, wie Sie dies vermeiden können.

Wir werden beide Methoden mit Speedtasks demonstrieren.sava, von denen ein Teil unten gezeigt wird.

Unsere Hauptforschungsfrage istwelche der Reaktionszeitvariablen ist wahrscheinlich
normalverteilt in unserer Bevölkerung?Diese Daten sind ein Lehrbuchbeispiel dafür, warum Sie Ihre Daten gründlich überprüfen sollten, bevor Sie mit der Bearbeitung oder Analyse beginnen. Lassen Sie uns genau das tun und einige Histogramme aus der folgenden Syntax ausführen.

Ergebnis

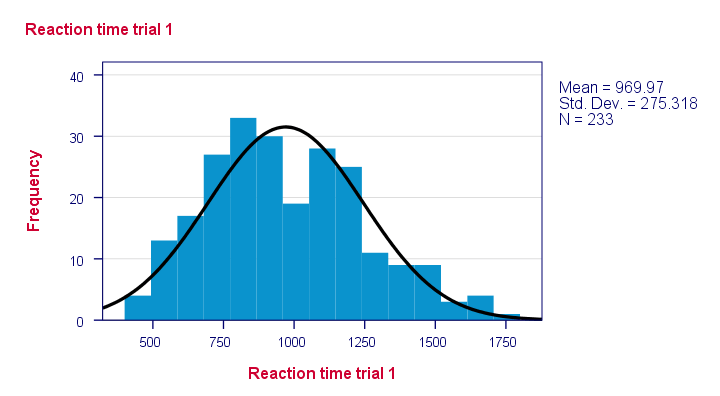
Beachten Sie, dass einige Verteilungen überhaupt nicht plausibel aussehen. Aber welche sind wahrscheinlich normalverteilt?

SPSS Kolmogorov-Smirnov-Test aus NPAR-TESTS

Unsere bevorzugte Option für die Ausführung des Kolmogorov-Smirnov-Tests ist underAnalyze Nichtparametrische Tests Legacy-Dialoge 1-Beispiel K-S… wie unten gezeigt.

Als nächstes füllen wir einfach den Dialog aus, wie unten gezeigt.

Wenn Sie auf Einfügen klicken, wird die folgende Syntax angezeigt. Lass es uns laufen.

Kolmogorov-Smirnov-Testsyntax aus nichtparametrischen Tests

Ergebnisse

Beachten Sie zunächst, dass die Teststatistik für unsere erste Variable 0,073 ist – genau wie wir es etwas früher in unserem Diagramm der kumulativen relativen Häufigkeiten gesehen haben. Das Diagramm enthält genau die gleichen Daten, mit denen wir gerade unseren Test durchgeführt haben, sodass diese Ergebnisse gut konvergieren.
Zu unserer Forschungsfrage: Nur die Reaktionszeiten für Versuch 4 scheinen normalverteilt zu sein.

SPSS Kolmogorov-Smirnov-Test aus VARIABLEN UNTERSUCHEN

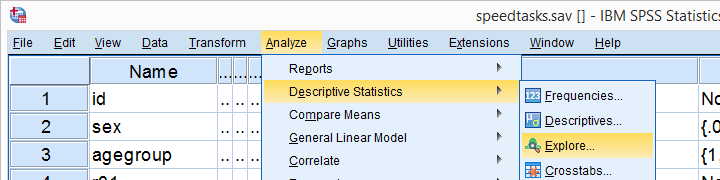
Eine alternative Möglichkeit, den Kolmogorov-Smirnov-Test auszuführen, beginnt mit Analyze Descriptive Statistics Explorewie unten gezeigt.

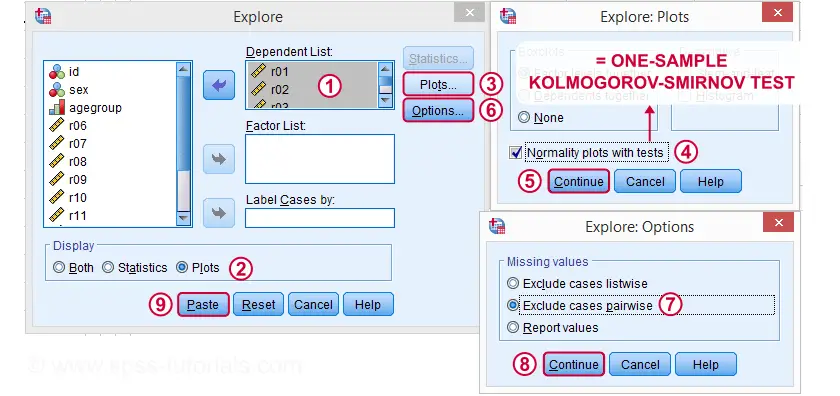
Kolmogorov-Smirnov-Testsyntax aus nichtparametrischen Tests

Results

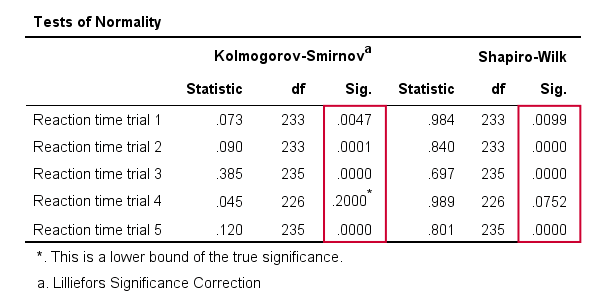
As a rule of thumb, we conclude thata variable is not normally distributed if „Sig.” < 0.05.So deuten sowohl der Kolmogorov-Smirnov-Test als auch der Shapiro-Wilk-Test darauf hin, dass nur der Reaktionszeitversuch 4 einer Normalverteilung in der gesamten Population folgt.
Beachten Sie außerdem, dass die Ergebnisse des Kolmogorov-Smirnov-Tests mit denen von NPAR-TESTS identisch sind.

Meldung eines Kolmogorov-Smirnov-Tests

Um unsere Testergebnisse nach APA-Richtlinien zu melden, schreiben wir etwas wie“Ein Kolmogorov-Smirnov-Test zeigt an, dass die Reaktionszeiten in Versuch 1 keiner Normalverteilung folgen, D (233) = 0,07, p = 0,005.“Versuchen Sie für zusätzliche Variablen, dies zu verkürzen, aber stellen Sie sicher, dass Sie

• D (für „Differenz“), die Kolmogorov-Smirnov-Teststatistik,
• df, die Freiheitsgrade (die gleich N sind) und
• p , die statistische Signifikanz.

Falsche Ergebnisse in SPSS?

Wenn Sie ein Student sind, der nur einen Test bestehen möchte, können Sie jetzt aufhören zu lesen. Befolgen Sie einfach die Schritte, die wir bisher besprochen haben, und Sie werden gut sein.

Richtig, lassen Sie uns jetzt genau dieselben Tests in SPSS Version 18 erneut ausführen und uns die Ausgabe ansehen.

In dieser Ausgabe sind die exakten p-Werte enthalten und liegen – zum Glück – sehr nahe an den asymptotischen p-Werten. Weniger erfreulich ist jedoch, dass sich die Ergebnisse der SPSS-Version 18 stark von den Ergebnissen der SPSS-Version 24 unterscheiden, die wir bisher gemeldet haben.
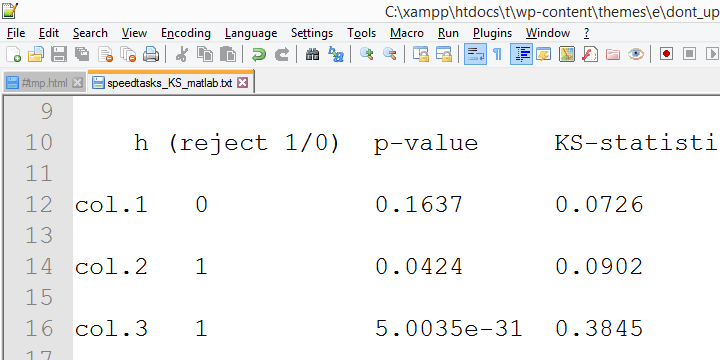
Der Grund scheint die Lilliefors-Signifikanzkorrektur zu sein, die in neueren SPSS-Versionen angewendet wird. Das Ergebnis scheint zu sein, dass die asymptotischen Signifikanzniveaus viel mehr von der genauen Signifikanz abweichen als wenn die Korrektur nicht impliziert ist. Dies wirft ernsthafte Zweifel an der Richtigkeit der „Lilliefors-Ergebnisse“ auf – der Standard in neueren SPSS-Versionen.Konvergierende Beweise für diesen Vorschlag wurden von meinem Kollegen Alwin Stegeman gesammelt, der alle Tests in Matlab erneut durchführte. Die Matlab-Ergebnisse stimmen mit den SPSS 18-Ergebnissen und damit nicht mit den neueren Ergebnissen überein.

Kolmogorov-Smirnov-Normalitätstest – Begrenzte Nützlichkeit

Der Kolmogorov-Smirnov-Test dient häufig zum Testen der Normalitätsannahme, die für viele statistische Tests wie ANOVA, den t-Test und viele andere erforderlich ist. Es wird jedoch fast routinemäßig übersehen, dass solche Tests robust gegen eine Verletzung dieser Annahme sind, wenn Stichprobengrößen angemessen sind, sagen wir N ≥ 25.Der zugrunde liegende Grund dafür ist der zentrale Grenzwertsatz. Daher sind Normalitätstests nur für kleine Stichprobengrößen erforderlich, wenn die Normalitätsannahme erfüllt werden soll.Leider führen kleine Stichprobengrößen zu einer geringen statistischen Aussagekraft für Normalitätstests. Dies bedeutet, dass wesentliche Abweichungen von der Normalität nicht zu statistischer Signifikanz führen. Der Test sagt, dass es keine Abweichung von der Normalität gibt, obwohl es tatsächlich riesig ist. Kurz gesagt, die Situation, in der Normalitätstests erforderlich sind – kleine Stichprobengrößen -, ist auch die Situation, in der sie schlecht abschneiden.

Danke fürs Lesen.