Teil 4B: Tensoren, Skalare, Vektoren und Matrizen
Ein Tensor ist ein Array von Daten (Zahlen, Funktionen usw.), die in einer beliebigen Anzahl (0 und größer) von Dimensionen erweitert wird. Die Anzahl der Dimensionen wird als Rang des Tensors bezeichnet.
Rang 0 Tensor
Ein Tensor ohne Dimensionen (0).
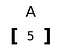
Rang 1 Tensor
Ein Tensor, der nur in einer Dimension erweitert wird.
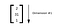

Rank 2 tensor
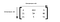
Rank 3 tensor

As shown in figure, a rank 3 tensor has a cube (or cuboid like structure).
If rank of a tensor exceeds 3, it becomes difficult to visualize.
Skalar
Ein Skalar ist ein 0-Rang-Tensor. In der Physik werden verschiedene Größen als Skalar dargestellt, z. B. Entfernung (500 km), Temperatur (10ºC), Geschwindigkeit (34 km / h) usw.
Vektor
Ein Rang-1-Tensor wird als Vektor bezeichnet. Physikalische Größen wie Geschwindigkeit (10 m / s), Verschiebung (54 m nach Osten), Elektromagnetisches Feld (1 V / m).
Unterschied zwischen Skalar und Vektor :
Eine Größe, die keine zusätzlichen Informationen (z. B. Richtung) benötigt (z. B. Temperatur), wird als skalar dargestellt. Wohingegen eine Größe, deren Richtung neben ihrer Größe angegeben werden muss, mit einem Vektor (wie elektrisches Feld) dargestellt wird.
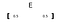
Ein Vektor wird mit einem fetten Buchstaben (wie „E“ ) oder einem Pfeil über dem Buchstaben bezeichnet.
Um einen Vektor zu zeichnen, verwenden wir seine Elemente als Koordinatenwert (x-, y- und z-Achse). Hier wird das erste Element (0,5) als x-Wert und das zweite Element (ebenfalls 0,5) als y-Wert verwendet (wenn wir drei Elemente hätten, wäre das dritte der z-Wert gewesen).

Nachdem wir den Vektor als Punkt gezeichnet haben, setzen wir einen Pfeil vom Ursprung (0,0) darauf.
Ein Vektor ist einfach eine Matrix, die entweder eine Zeile (Spaltenvektor genannt) oder eine Spalte (Zeilenvektor genannt) hat.
Matrix
Eine Matrix ist ein Rang-2-Tensor. Wir haben uns Matrix bereits angesehen.
Ein Tensor mit einem Rang größer als 2 wird einfach „Tensor“ genannt (es gibt keinen spezifischen Namen für Tensoren mit einem Rang größer als 2).Das Konzept des Tensors verallgemeinert die Matrizen, Vektoren und Skalare unter einem Dach (sie alle sind Tensoren, aber mit unterschiedlichen Rängen).
Matrizen als Produkt von Vektoren :
Wenn zwei Vektoren multipliziert werden, bilden sie eine Matrix.


Vector X and Y combined, have 6 elements but their product alone has 9 elements. Somit könnten einige Matrizen als Produkt zweier Vektoren zerlegt werden.
Leave a Reply