Análisis de regresión > Homocedasticidad / Homogeneidad de Varianza / Supuesto de Igual Varianza

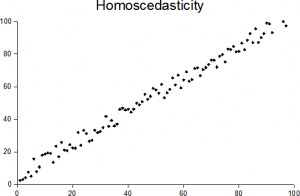
Imagen: Sreebot| Wikimedia Commons

En pocas palabras, homoscedasticidad significa «tener la misma dispersión.»Para que exista en un conjunto de datos, los puntos deben estar aproximadamente a la misma distancia de la línea, como se muestra en la imagen de arriba. Lo opuesto es la heterocedasticidad («dispersión diferente»), donde los puntos están a distancias muy variables de la línea de regresión.

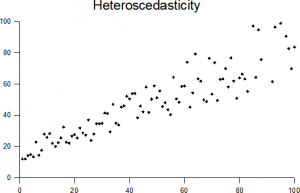
Los puntos más altos en el eje x tienen una varianza mayor que los valores más pequeños.

Tenga en cuenta que he dicho «distancia» aquí y no varianza. Al ver un gráfico, es más fácil observar las distancias desde los puntos hasta la línea para determinar si un conjunto de datos muestra homocedasticidad. Técnicamente, es la varianza lo que cuenta, y eso es lo que usarías en los cálculos. Sin embargo, como la varianza requiere una fórmula, es imposible observar un gráfico.

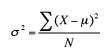
Fórmula de varianza.

Como la varianza es solo la desviación estándar al cuadrado, también puede ver homocedasticidad descrita como una condición en la que las desviaciones estándar son iguales para todos los puntos.

En términos más formales

Rara vez se encontrará con un conjunto de datos que tenga una varianza de cero. Es más probable que vea variaciones que van desde 0.01 a 101.01. Entonces, ¿cuándo se clasifica un conjunto de datos como que tiene homocedasticidad? La regla general1 es:

Si la relación entre la varianza más grande y la varianza más pequeña es 1,5 o inferior, los datos son homocedásticos.

¿Cuál es el Supuesto de Varianza igual?

La suposición de varianzas iguales (es decir, la suposición de homocedasticidad) asume que diferentes muestras tienen la misma varianza, incluso si provienen de diferentes poblaciones. La suposición se encuentra en muchas pruebas estadísticas, incluido el Análisis de Varianza (ANOVA) y la Prueba T de Student. Otras pruebas, como la prueba T de Welch, no requieren variaciones iguales en absoluto.Realizar una prueba sin verificar variaciones iguales puede tener un impacto significativo en sus resultados e incluso puede invalidarlos por completo. La medida en que se vean afectados sus resultados depende de la prueba que utilice y de la sensibilidad de esa prueba a las variaciones desiguales. Por ejemplo, si bien una prueba de ANOVA de factor fijo con tamaños de muestra iguales solo se ve afectada en una pequeña cantidad, una ANOVA con tamaños de muestra desiguales podría darle resultados completamente inválidos.

La asunción de varianzas iguales también se utiliza en la regresión lineal, que asume que los datos son homocedásticos. En términos simples, si sus datos están ampliamente difundidos (como en forma de cono en la imagen heterocedástica de arriba), la regresión no funcionará tan bien. Para obtener más información sobre este tema, consulte Suposiciones & Condiciones de regresión.

La prueba de Homogeneidad de Varianza

Las pruebas que puede ejecutar para verificar que sus datos cumplan con esta suposición incluyen:

• La Prueba de Bartlett
• la Prueba M de Box
• La prueba Brown-Forsythe
• La prueba Fmax de Hartley
• La Prueba de Levene

——————————————————————————

Necesito ayuda con una tarea o cuestión de prueba? Con Chegg Study, puede obtener soluciones paso a paso a sus preguntas de un experto en el campo. ¡Tus primeros 30 minutos con un tutor de Chegg son gratis!