El artículo mencionado a continuación proporciona una vista cercana de la Función de Producción de Cobb-Douglas.

La función de producción de Cobb-Douglas se basa en el estudio empírico de la industria manufacturera estadounidense realizado por Paul H. Douglas y C. W. Cobb. Es una función de producción lineal homogénea de grado uno que tiene en cuenta dos insumos, trabajo y capital, para toda la producción de la .industria manufacturera.

La función de producción de Cobb-Douglas se expresa como:

Q = ALa Cß

donde Q es salida y L y С son entradas de trabajo y capital respectivamente. A, a y β son parámetros positivos donde = a > O, β > O.

La ecuación dice que la salida depende directamente de L y C, y que la parte de la salida que no se puede explicar por L y С se explica por A que es el ‘residual’, a menudo llamado cambio técnico.

La función de producción resuelta por Cobb-Douglas tuvo una contribución de 1/4 de capital al aumento de la industria manufacturera y 3/4 de mano de obra, de modo que la función de producción C-D es

Q = AL3/4 C1/4

que muestra retornos constantes a escala porque el total de los valores de L y С es igual a uno: (3/4 + 1/4), es decir, (a + β = 1) . El coeficiente de mano de obra en la función C-D mide el aumento porcentual en (Q que resultaría de un aumento del 1% en L, manteniendo constante С.

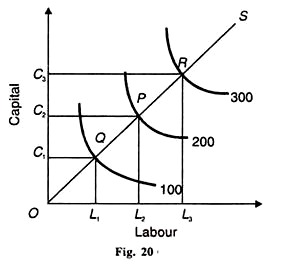
Del mismo modo, В es el aumento porcentual en Q que resultaría de un aumento del 1% en C, manteniendo L como constante. La función de producción C-D que muestra retornos constantes a escala se muestra en la Figura 20. La mano de obra se toma en el eje horizontal y el capital en el eje vertical.

Para producir 100 unidades de producción, se utilizan ОС, unidades de capital y otras unidades de trabajo. Si la producción se duplicara a 200, los insumos de trabajo y capital tendrían que duplicarse. ОС es exactamente el doble de ОС1 y de OL2 es el doble de OL2.

del mismo modo, si la salida será levantado tres veces a 300, las unidades de trabajo y el capital tendrá que ser mayor de tres veces. OC3 y OL3 son tres veces más grandes que ОС1 y OL1, respectivamente. Otro método es tomar la línea de escala o ruta de expansión que conecta los puntos de equilibrio Q, P y R. OS es la línea de escala o ruta de expansión que une estos puntos.

Muestra que las isocuantas 100, 200 y 300 son equidistantes. Por lo tanto, en la línea de escala OS OQ = QP = PR, que muestra que cuando el capital y el trabajo aumentan en proporciones iguales, la producción también aumenta en la misma proporción.

Críticas a la Función de Producción C-D:

La función de producción C-D ha sido criticada por Arrow, Chenery, Minhas y Solow como se explica a continuación:

1. La función de producción C-D considera solo dos insumos, trabajo y capital, y descuida algunos insumos importantes, como las materias primas, que se utilizan en la producción. Por lo tanto, no es posible generalizar esta función a más de dos entradas.

2. En la función de producción C-D, el problema de la medición del capital surge porque solo toma la cantidad de capital disponible para la producción. Pero el uso pleno del capital disponible sólo puede hacerse en períodos de pleno empleo. Esto no es realista porque ninguna economía está siempre a pleno empleo.

3. La función de producción C-D es criticada porque muestra retornos constantes a escala. Pero los rendimientos constantes a escala no son una realidad, ya que los rendimientos a escala crecientes o decrecientes son aplicables a la producción.

No es posible cambiar todos los insumos para lograr un cambio proporcional en los productos de todas las industrias. Algunos insumos son escasos y no pueden aumentarse en la misma proporción que los insumos abundantes. Por otro lado, insumos como máquinas, emprendimiento, etc. son indivisibles. A medida que aumenta la producción debido al uso de factores indivisibles a su capacidad máxima, disminuye el costo unitario.

Por lo tanto, cuando el suministro de insumos es escaso y las indivisibilidades están presentes, no son posibles retornos constantes a escala. Cada vez que se aumentan las unidades de diferentes insumos en el proceso de producción, las economías de escala y la especialización conducen a un aumento de los rendimientos a escala.

En la práctica, sin embargo, a ningún empresario le gustaría aumentar las diversas unidades de insumos para obtener un aumento proporcional de la producción. Su esfuerzo es lograr un aumento más que proporcional de la producción, aunque tampoco se descarta la disminución de los rendimientos a escala.

4. La función de producción C-D se basa en el supuesto de la sustituibilidad de los factores y descuida la complementariedad de los factores.

5. Esta función se basa en el supuesto de una competencia perfecta en el mercado de factores que no es realista. Sin embargo, si se elimina esta suposición, los coeficientes α y β no representan las partes de los factores.

6. Una de las debilidades de la función C-D es el problema de agregación. Este problema surge cuando esta función se aplica a todas las empresas de una industria y a toda la industria. En esta situación, habrá muchas funciones de producción de agregación baja o alta. Por lo tanto, la función C-D no mide lo que pretende medir.

Conclusión:

Por lo tanto, la viabilidad de la función de producción de Cd en la industria manufacturera es una propuesta dudosa. Esto no es aplicable a la agricultura, donde para el cultivo intensivo, el aumento de las cantidades de insumos no aumentará proporcionalmente la producción. Incluso entonces, no se puede negar que los rendimientos constantes a escala son una etapa en la vida de una empresa, industria o economía. Es otra cosa que esta etapa pueda llegar después de algún tiempo y por un corto tiempo.

Es importante:

A pesar de estas críticas, la función C-D es de mucha importancia.

1. Se ha utilizado ampliamente en estudios empíricos de industrias manufactureras y en comparaciones entre industrias.

2. Se utiliza para determinar la proporción relativa de mano de obra y capital en la producción total.

3. Se utiliza para probar el teorema de Euler.

4. Sus parámetros a y b representan coeficientes de elasticidad que se utilizan para comparaciones intersectoriales.

5. Esta función de producción es lineal homogénea de grado uno que muestra retornos constantes a escala, Si α + β = 1, hay retornos crecientes a escala y si α + β < 1, hay retornos decrecientes a escala.

6. Los economistas han extendido esta función de producción a más de dos variables.