Articles

Notación de función y Cómo Evaluar una Función

by admin

La notación común de una función generalmente se escribe como,

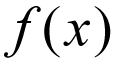
f(x) significa que f es una expresión que involucra la variable x

No pienses en esto demasiado literalmente, es decir, f se multiplica a x. En su lugar, considere esto como una expresión matemática que se lee como

f es una función de x

O

f es una expresión que contiene la variable o la letra x

las Funciones también pueden ser escritos en diferentes maneras con otras variables tales como

  • g(x), h(x) y k(x)

además, las funciones pueden tomar otros valores de entrada que no sean x.

  • f(a), h(r) y k(m)

La idea clave es recordar siempre que la variable fuera del paréntesis es el «nombre» de la función, mientras que la variable dentro del paréntesis es el valor de entrada de la función.

Por ejemplo, el siguiente se llama a la función k con un valor de entrada de m.

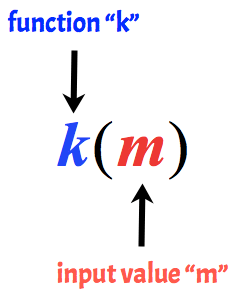
k(m) se puede leer como la función de k de m. eso significa que la función k se expresa en términos de m, ya que m es el valor de entrada.

Básico Ejemplos de Evaluación de Funciones

Ejemplo 1: Evaluar la función .

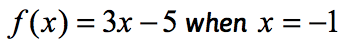
f(x) = 3x - 5 cuando x=-1

Esta es la notación normal de función donde la función es f mientras que el valor de entrada es x. Para evaluar una función, lo que queremos es sustituir cada instancia de x en la expresión y luego simplificar.

Desde x = – 1, sustituimos este valor en la función y simplificamos. Al hacerlo, obtenemos una solución que se ve así.

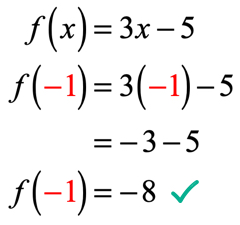
f(x) = 3x - 1 → f(-1) = 3(-1) - 5 → f(-1) = -3 -5 = -8. por lo tanto, f(-1) = -8.

Ejemplo 2: Evaluar la función .

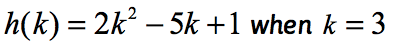
h(k) = 2k^2-5k+1 cuando k=3

Observe que la función aquí es h y el valor de la entrada es k. Al igual que en nuestro ejemplo anterior, queremos sustituir cualquier valor numérico asignado a k en la función dada, y simplificar.

a partir de k = 3, la solución debe ser similar a esto

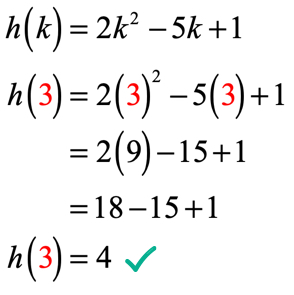
h(k) = 2k^2 - 5k + 1 → h(3) = 2(3)^2 - 5(3) + 1 → h(3) = 2(9) -15+1 → h(3) = 18 - 15 + 1 → h(3) = 4.

Ejemplo 3: Evalúe cada valor de x en la tabla de abajo usando la función de abajo. Trace los puntos en el eje xy y conecte los puntos para revelar el gráfico de la función.

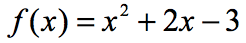
f(x) = x^2 + 2x - 3
una tabla de valores para la función f de x o f(x), donde los valores de x son -4, -3, -2, -1, 0, 1 y 2

Ya hay siete x-entradas, que significa que vamos a evaluar la función de siete veces. Trate de resolver esto por su cuenta y luego regrese para verificar sus respuestas.

Si lo ha hecho correctamente, estos son los valores:

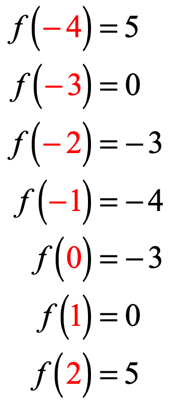
estos son los valores de la función cuando se evalúan con cada valor x o valor de entrada. f(-4) = 5, f(-3) = 0, f(-2)=-3, f(-1) = -4, f(0) = -3, f(1) = 0, f(2) = 5.

ahora podemos colocar los valores de salida en la tabla.

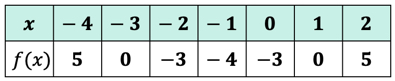
aquí está la tabla de valores representados como un conjunto de pares ordenados: { (-4,5), (-3,0), (-2,-3), (-1,-4), (0,-3), (1,0), (2,5) }

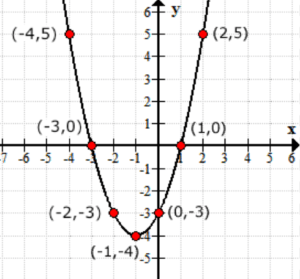
Creo que de los valores de salida de la función f\left( x \right) como los valores. Así es como se ve el gráfico en el eje xy.

después de trazar los puntos de la tabla generados por la función f(x) = x^2 + 2x -3,obtenemos una parábola que se abre con un mínimo en (-1, -4), intersección en y de -3 e intercepciones x de -3 y 1.

Ejemplos intermedios de Funciones de evaluación

Ejemplo 4: Dado que g\left( x \right) = {x^2} – 3x + 1, busque g\left( {2x – 1} \right).

En ejemplos anteriores, hemos estado evaluando una función por un número. Esta vez el valor de entrada ya no es un valor numérico fijo, sino una expresión. Puede parecer complicado, pero el procedimiento sigue siendo el mismo.

Reemplazaremos cada instancia de x en g \ left (x \right) por el valor de entrada que es 2x – 1. Simplifique cuadrando el binomio, aplicando la propiedad distributiva y combinando términos similares.

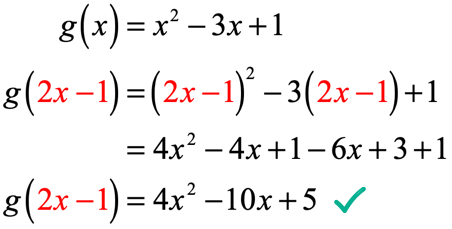
g(x)=x^2-3x+1 → g(2x-1) = (2x-1)^2 - 3(2x-1) +1 → g(2x-1) = 4x^2-4x+1-6x+3=1 → g(2x-1) = 4x^2 - 10x + 5

Ejemplo 5: Dado que p\left( x \right) = {{4x – 1} \over x} , evaluar p\left( 1 \derecho) – p\left( { – 1} \derecho).

El problema puede parecer intimidante al principio, pero una vez que lo analizamos y aplicamos lo que ya sabemos sobre cómo evaluar funciones, ¡esto no debería ser tan malo!

Lo que tenemos que hacer aquí es evaluar la función en x = 1 y luego restar por el valor de la función cuando se evalúa en x= -\, 1.

Tenga mucho cuidado al sustituir los valores y durante el proceso de simplificación. Si no tiene cuidado en cada paso, es muy fácil cometer errores cuando suma, resta, multiplica o divide números positivos y negativos.

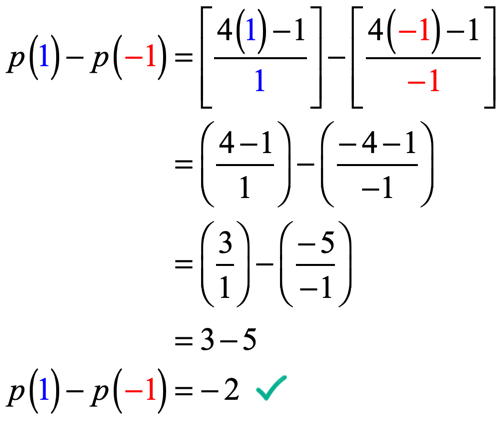
p(1) - p(-1) = { /(1) } - { /(-1) } = - = 3-5 → p(1) - p(-1) = -2

Ejemplo Avanzado de la Aplicación del Concepto de Evaluación de Funciones

Ejemplo 6: Si f\left( 2 \derecho) = 9, hallar el valor de a en la función siguiente.

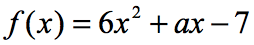
f(x) = 6x^2 + ax -7, encontrar el valor de un

En la ecuación, f\left( 2 \derecho) = 9, nos dice que si la entrada de la función es 2; la salida de la función será 9. Dado que la función se nos da, nuestro primer movimiento es al menos sustituir el valor de 2 y luego simplificar. Esto es lo que conseguiremos.

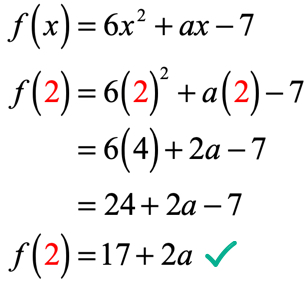
f(x) = 6x^2 + ax - 7 → f(2) = 6(2)^2 + a (2) - 7 → f(2) = 6(4) +2a - 7 = 24 + 2a - 7 → f(2) = 17 + 2a

la salida de La función después de evaluar en x = 2 es 17 + 2a. Recuerde, también se nos dice que la salida es de 9 uso de la ecuación dada f\left( 2 \derecho) = 9. Por lo tanto, lo que tenemos que hacer ahora es establecerlos iguales entre sí y resolver la ecuación lineal para el valor desconocido de a.

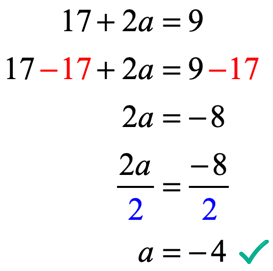
17 + 2a = 9 → 17-17+2a = 9-17 → 2a = -8 → (2a)/2 = -8/2 → a= -4

Vamos a verificar si el valor de a = – \,4 en f(x) = 6{x^2} + ax – 7 puede hacer que la condición dada f\left( 2 \right) = 9 sea una declaración verdadera.

f(x) = 6x^2 - 4x -7 → f(2) = 6(2)^2 - 4(2) - 7 = 6(4) - 8- 7 = 24 - 8 - 7 → f(2) = 9

Es cierto! Por lo tanto, hemos resuelto con éxito el valor correcto de a.