Un tensor es una matriz de datos (números, funciones, etc.) que se expande en cualquier número (0 y mayor) de dimensiones. El número de dimensiones se llama rango de tensor.

Tensor de rango 0

Un tensor que no tiene dimensiones (0).

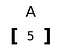
Rank 1 tensor

Un tensor que se expande en una sola dimensión.

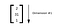
Rank 2 tensor

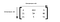
Rank 3 tensor

As shown in figure, a rank 3 tensor has a cube (or cuboid like structure).

If rank of a tensor exceeds 3, it becomes difficult to visualize.

Escalar

Un escalar es 0 rango del tensor. En física, varias cantidades se representan como un escalar, como: Distancia (500 km), Temperatura (10 ° C), Velocidad (34 km/h), etc.

Vector

Un tensor de rango 1 se denomina vector. Cantidades físicas como Velocidad (10 m/s), Desplazamiento (54 m hacia el Este), Campo electromagnético (1 V/m).

Diferencia entre escalar y vector :

Una cantidad que no requiere información adicional (como la dirección) con ella (como la temperatura) se representa como escalar. Mientras que, una cantidad que necesita que se especifique la dirección junto con su magnitud se representa con un vector (como, campo eléctrico).

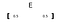
Un vector se denota con la letra negrita (como «E» ) o una flecha por encima de la carta.

Para trazar un vector utilizamos sus elementos como el valor de coordenadas (eje x, y y z respectivamente). Aquí, el primer elemento (0.5) se toma como valor x y el segundo elemento (también, 0.5) se toma como valor y (si tuviéramos tres elementos, el tercero habría sido el valor z).

Después de trazar el vector como un punto que poner una flecha a ella, desde el origen(0,0).

Un vector es simplemente una matriz que tiene una fila (llamada vector de columna) o una columna (llamada vector de fila).

Matriz

Una matriz es un tensor de rango 2. Hemos mirado Matrix antes.

Un tensor con rango mayor que 2 se llama simplemente «tensor» (no hay un nombre específico para tensores con rango mayor que 2).

El concepto de tensor generaliza las matrices, vectores y escalares bajo un mismo techo (todos son tensores pero con diferentes rangos).

Matrices como producto de vectores:

Cuando se multiplican dos vectores, forman una matriz.

Vector X and Y combined, have 6 elements but their product alone has 9 elements. Por lo tanto, algunas matrices podrían desglosarse como un producto de dos vectores.