Una prueba de normalidad alternativa es la prueba de Shapiro-Wilk.

• ¿Qué es una prueba de normalidad de Kolmogorov-Smirnov?
• Prueba SPSS Kolmogorov-Smirnov de las PRUEBAS NPAR
• Prueba SPSS Kolmogorov-Smirnov de EXAMINAR VARIABLES
• Informe de una prueba Kolmogorov-Smirnov
• Resultados incorrectos en SPSS?

¿Qué es una prueba de normalidad de Kolmogorov-Smirnov?

La prueba de Kolmogorov-Smirnov examina si es probable que los puntajes sigan alguna distribución en alguna población.Para evitar confusiones, hay 2 pruebas de Kolmogorov-Smirnov:

• hay una muestra de prueba de Kolmogorov-Smirnov para probar si una variable sigue una distribución dada en una población. Esta» distribución dada «es generalmente-no siempre – la distribución normal, por lo tanto»Prueba de normalidad de Kolmogorov-Smirnov».
• también está la prueba de muestras independientes (mucho menos común) de Kolmogorov-Smirnov para probar si una variable tiene distribuciones idénticas en 2 poblaciones.

En teoría, «prueba de Kolmogorov-Smirnov» podría referirse a cualquiera de las pruebas (pero generalmente se refiere a la prueba de Kolmogorov-Smirnov de una muestra) y es mejor evitarla. Por cierto, ambas pruebas de Kolmogorov-Smirnov están presentes en SPSS.

Prueba de Kolmogorov-Smirnov-Ejemplo simple

Así que digamos que tengo una población de 1,000,000 de personas. Creo que sus tiempos de reacción en alguna tarea están perfectamente distribuidos normalmente. Muestro a 233 de estas personas y mido sus tiempos de reacción.
Ahora la distribución de frecuencia observada de estos probablemente diferirá un poco, pero no demasiado, de una distribución normal. Así que corro un histograma sobre los tiempos de reacción observados y superpongo una distribución normal con la misma media y desviación estándar. El resultado se muestra a continuación.

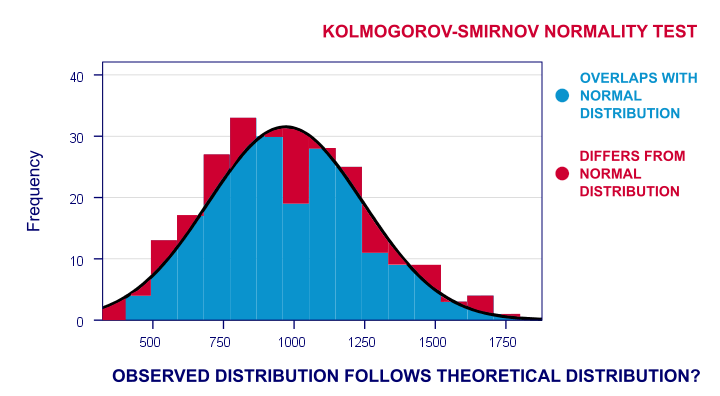
La distribución de frecuencia de mis puntuaciones no se superpone completamente con mi curva normal. Ahora, podría calcular el porcentaje de casos que se desvían de la curva normal, el porcentaje de áreas rojas en el gráfico. Este porcentaje es una estadística de prueba: expresa en un solo número cuánto difieren mis datos de mi hipótesis nula. Por lo tanto, indica en qué medida las puntuaciones observadas se desvían de una distribución normal.
Ahora, si mi hipótesis nula es verdadera, entonces este porcentaje de desviación probablemente debería ser bastante pequeño. Es decir, una pequeña desviación tiene un valor de probabilidad alto o valor p.A la inversa, un porcentaje de desviación enorme es muy improbable y sugiere que mis tiempos de reacción no siguen una distribución normal en toda la población. Así que una desviación grande tiene un valor p bajo. Como regla general, se proyectaba la hipótesis nula si p < 0.05.So si p < 0,05, no creemos que nuestra variable siga una distribución normal en nuestra población.

Prueba de Kolmogorov-Smirnov-Estadística de prueba

Así que esa es la forma más fácil de entender cómo funciona la prueba de normalidad de Kolmogorov-Smirnov. Computacionalmente, sin embargo, funciona de manera diferente: compara las frecuencias relativas acumulativas observadas con las esperadas, como se muestra a continuación.

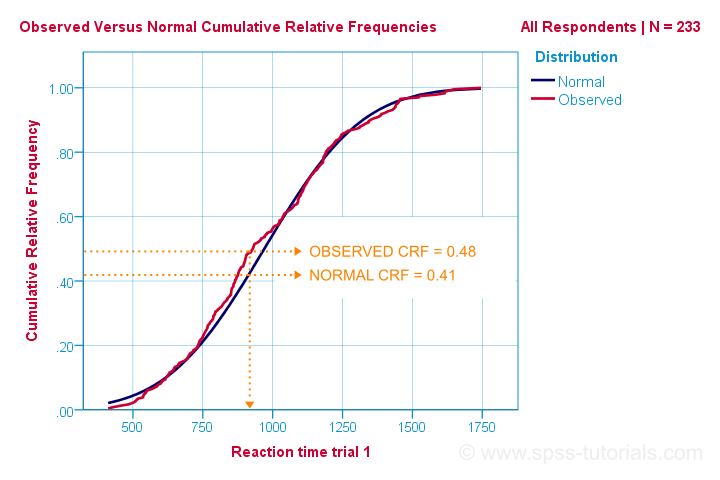
La prueba de Kolmogorov – Smirnov utiliza la diferencia absoluta máxima entre estas curvas como su estadística de prueba denotada por D. En este gráfico, la diferencia absoluta máxima D es (0.48-0.41 =) 0.07 y ocurre en un tiempo de reacción de 960 milisegundos. Tenga en cuenta que D = 0.07, ya que lo encontraremos en nuestra salida SPSS en un minuto.

La prueba de Kolmogorov-Smirnov en SPSS

Hay 2 formas de ejecutar la prueba en SPSS:

• PRUEBAS NPAR como se encuentran en Analizar Pruebas no paramétricas Diálogos heredados 1-Sample K-S… es nuestro método de elección porque crea una salida bien detallada.
• EXAMINAR VARIABLES desde Analizar Estadísticas descriptivas Explorar es una alternativa. Este comando ejecuta tanto la prueba Kolmogorov-Smirnov como la prueba de normalidad Shapiro-Wilk.
  Tenga en cuenta que EXAMINE VARIABLES utiliza la exclusión listwise de los valores faltantes de forma predeterminada. Así que si pruebo 5 variables, mis 5 pruebas solo usan casos que no tienen ningún error en ninguna de estas 5 variables. Por lo general, esto no es lo que quieres, pero te mostraremos cómo evitarlo.

Demostraremos ambos métodos usando tareas rápidas.sav en todo, parte del cual se muestra a continuación.

Nuestra principal pregunta de investigación es ¿cuál de las variables de tiempo de reacción es probable que se distribuya normalmente en nuestra población?Estos datos son un ejemplo de libro de texto de por qué debe inspeccionar a fondo sus datos antes de comenzar a editarlos o analizarlos. Vamos a hacer eso y ejecutar algunos histogramas de la sintaxis a continuación.

Result

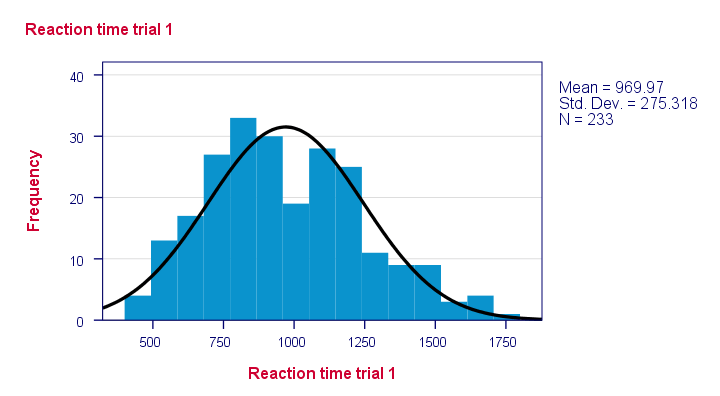
Tenga en cuenta que algunas distribuciones no parecen plausibles en absoluto. Pero, ¿cuáles se distribuirán normalmente?

Prueba SPSS Kolmogorov-Smirnov de PRUEBAS NPAR

Nuestra opción preferida para ejecutar la prueba Kolmogorov-Smirnov es analizar Pruebas no paramétricas Diálogos heredados 1-Muestra de K-S… como se muestra a continuación.

A continuación, rellenamos el cuadro de diálogo como se muestra a continuación.

Al hacer clic en Pegar, se muestra la sintaxis siguiente. Vamos a comprobarlo.

Sintaxis de prueba de Kolmogorov-Smirnov de pruebas no paramétricas

Resultados

En primer lugar, tenga en cuenta que la estadística de prueba para nuestra primera variable es 0.073, al igual que vimos en nuestro gráfico de frecuencias relativas acumulativas un poco antes. El gráfico contiene exactamente los mismos datos con los que acabamos de ejecutar nuestra prueba, por lo que estos resultados convergen muy bien.Con respecto a nuestra pregunta de investigación: solo los tiempos de reacción para el ensayo 4 parecen estar distribuidos normalmente.

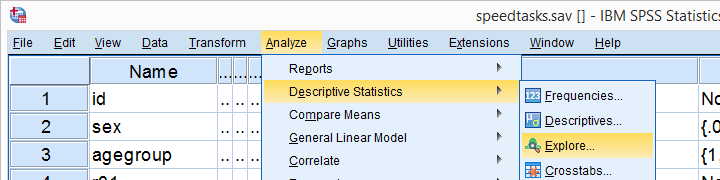
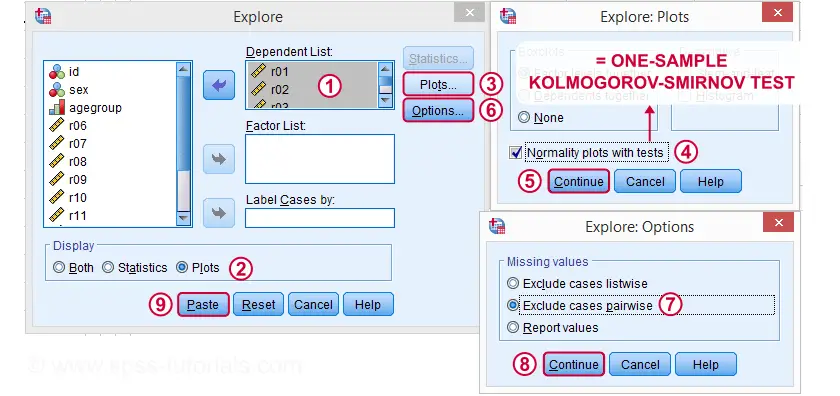
Prueba SPSS Kolmogorov-Smirnov de EXAMINAR VARIABLES

Una forma alternativa de ejecutar la prueba Kolmogorov-Smirnov comienza desde Analizar Estadística descriptiva Exploreas que se muestran a continuación.

Sintaxis de prueba Kolmogorov-Smirnov de pruebas no paramétricas

Results

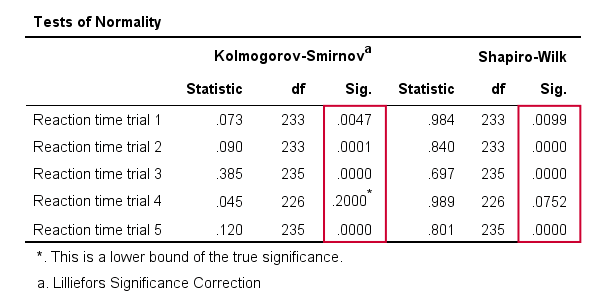
As a rule of thumb, we conclude thata variable is not normally distributed if «Sig.” < 0.05.Por lo tanto, tanto la prueba de Kolmogorov-Smirnov como los resultados de la prueba de Shapiro-Wilk sugieren que solo el ensayo de tiempo de reacción 4 sigue una distribución normal en toda la población.Además, tenga en cuenta que los resultados de la prueba de Kolmogorov-Smirnov son idénticos a los obtenidos de las PRUEBAS NPAR.

Reportar una prueba de Kolmogorov-Smirnov

Para reportar los resultados de nuestras pruebas siguiendo las pautas de la APA, escribiremos algo como»una prueba de Kolmogorov-Smirnov indica que los tiempos de reacción en el ensayo 1 no siguen una distribución normal, D(233) = 0.07, p = 0.005.»Para variables adicionales, intente acortar esto, pero asegúrese de incluir

• D (para «diferencia»), el estadístico de prueba de Kolmogorov-Smirnov,
• df, los grados de libertad (que es igual a N) y
• p, la significación estadística.

¿Resultados incorrectos en SPSS?

Si eres un estudiante que solo quiere aprobar un examen, puedes dejar de leer ahora. Solo sigue los pasos que hemos discutido hasta ahora y estarás bien.

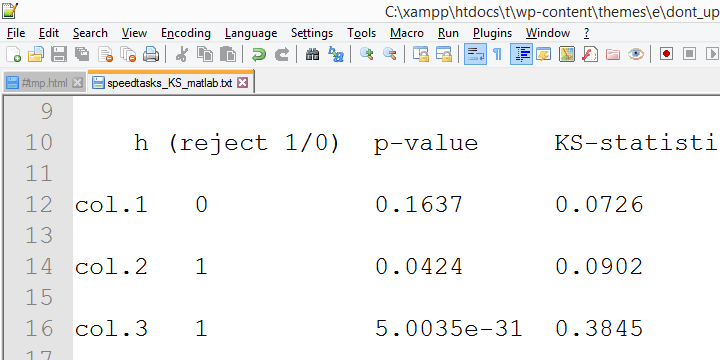
Bien, ahora ejecutemos las mismas pruebas exactas de nuevo en la versión 18 de SPSS y echemos un vistazo a la salida.

En esta salida, se incluyen los valores p exactos y, afortunadamente, están muy cerca de los valores p asintóticos. Sin embargo, menos afortunadamente,los resultados de la versión 18 del SPSS son muy diferentes de los resultados de la versión 24 del SPSS reportados hasta ahora.La razón parece ser la corrección de significación de Lilliefors que se aplica en las versiones más nuevas de SPSS. El resultado parece ser que los niveles de significación asintótica difieren mucho más de la significación exacta que cuando la corrección no está implícita. Esto plantea serias dudas con respecto a la corrección de los «resultados de Lilliefors», los predeterminados en las versiones SPSS más recientes.La evidencia convergente para esta sugerencia fue recopilada por mi colega Alwin Stegeman que volvió a analizar todas las pruebas en Matlab. Los resultados de Matlab concuerdan con los resultados de SPSS 18 y, por lo tanto, no con los resultados más recientes.

Prueba de normalidad de Kolmogorov-Smirnov: Utilidad limitada

La prueba de Kolmogorov-Smirnov es a menudo para probar el supuesto de normalidad requerido por muchas pruebas estadísticas como ANOVA, la prueba t y muchas otras. Sin embargo, casi rutinariamente se pasa por alto que tales pruebas son robustas contra una violación de esta suposición si los tamaños de muestra son razonables, digamos N ≥ 25.La razón subyacente de esto es el teorema del límite central. Por lo tanto, las pruebas de normalidad solo son necesarias para muestras de tamaño pequeño si el objetivo es satisfacer el supuesto de normalidad.Desafortunadamente, los tamaños de muestra pequeños dan como resultado un bajo poder estadístico para las pruebas de normalidad. Esto significa que las desviaciones sustanciales de la normalidad no darán lugar a significancia estadística. La prueba dice que no hay desviación de la normalidad mientras que en realidad es enorme. En resumen, la situación en la que se necesitan pruebas de normalidad-tamaños de muestra pequeños – también es la situación en la que funcionan mal.

Gracias por leer.