Analyse de régression >Homoscédasticité / Homogénéité de Variance / Hypothèse de Variance égale

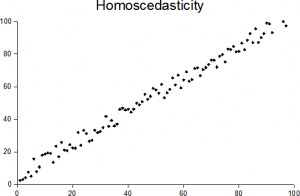
Image:Sreebot|Wikimedia Commons

En termes simples, l’homoscédasticité signifie « avoir la même dispersion.”Pour qu’il existe dans un ensemble de données, les points doivent être à peu près à la même distance de la ligne, comme indiqué dans l’image ci-dessus. Le contraire est l’hétéroscédasticité (« dispersion différente »), où les points sont à des distances très variables de la droite de régression.

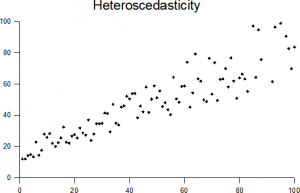
Les points les plus élevés sur l’axe des abscisses ont une variance plus grande que les valeurs plus petites.

Notez que j’ai dit « distance” ici et non variance. Lors de l’affichage d’un graphique, il est plus facile d’examiner les distances entre les points et la ligne pour déterminer si un ensemble de données présente une homoscédasticité. Techniquement, c’est la variance qui compte, et c’est ce que vous utiliseriez dans les calculs. Cependant, comme la variance nécessite une formule, il est impossible de regarder sur un graphique.

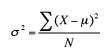
Formule de variance.

Comme la variance n’est que l’écart-type au carré, vous pouvez également voir l’homoscédasticité décrite comme une condition où les écarts-types sont égaux pour tous les points.

En termes plus formels

Vous rencontrerez rarement un ensemble de données dont la variance est nulle. Vous êtes plus susceptible de voir des variances allant de 0,01 à 101,01. Alors, quand un ensemble de données est-il classé comme ayant une homoscédasticité? La règle générale de base 1 est la suivante:

Si le rapport entre la plus grande variance et la plus petite variance est de 1,5 ou inférieur, les données sont homoscédastiques.

Quelle est l’hypothèse d’une variance égale?

L’hypothèse de variances égales (c’est-à-dire l’hypothèse de l’homoscédasticité) suppose que différents échantillons ont la même variance, même s’ils proviennent de populations différentes. L’hypothèse se retrouve dans de nombreux tests statistiques, y compris l’Analyse de la variance (ANOVA) et le test T de Student. D’autres tests, comme le test T de Welch, ne nécessitent pas du tout de variances égales.
Exécuter un test sans vérifier les variances égales peut avoir un impact significatif sur vos résultats et peut même les invalider complètement. La mesure dans laquelle vos résultats sont affectés dépend du test que vous utilisez et de la sensibilité de ce test aux variances inégales. Par exemple, alors qu’un test d’ANOVA à facteur fixe avec des tailles d’échantillon égales n’est affecté que d’une petite quantité, une ANOVA avec des tailles d’échantillon inégales peut vous donner des résultats complètement invalides.

L’hypothèse de variances égales est également utilisée en régression linéaire, qui suppose que les données sont homoscédastiques. En termes simples, si vos données sont largement diffusées (comme en forme de cône dans l’image hétéroscédastique ci-dessus), la régression ne fonctionnera pas si bien. Pour plus d’informations sur ce sujet, voir Conditions de régression des hypothèses &.

Test d’homogénéité de variance

Les tests que vous pouvez exécuter pour vérifier que vos données répondent à cette hypothèse incluent:

• Test de Bartlett
• Test M de Box
• Test de Brown-Forsythe
• Test Fmax de Hartley
• Test de Levene

——————————————————————————

Besoin d’aide pour une question de devoirs ou de test? Avec Chegg Study, vous pouvez obtenir des solutions étape par étape à vos questions d’un expert dans le domaine. Vos 30 premières minutes avec un tuteur Chegg sont gratuites!