L’article mentionné ci-dessous fournit une vue rapprochée de la Fonction de production de Cobb-Douglas.

La fonction de production de Cobb-Douglas est basée sur l’étude empirique de l’industrie manufacturière américaine réalisée par Paul H. Douglas et C.W. Cobb. C’est une fonction de production linéaire homogène de degré un qui prend en compte deux intrants, le travail et le capital, pour l’ensemble de la production du.industrie manufacturière.

La fonction de production de Cobb-Douglas s’exprime par:

Q=ALa Cß

où Q est la sortie et L et С sont des entrées de travail et de capital respectivement. A, a et β sont des paramètres positifs où =a > O, β >O.

L’équation indique que la sortie dépend directement de L et C, et que la partie de la sortie qui ne peut pas être expliquée par L et С est expliquée par A qui est le « résiduel », souvent appelé changement technique.

La fonction de production résolue par Cobb-Douglas avait 1/4 de contribution de capital à l’augmentation de l’industrie manufacturière et 3/4 de main-d’œuvre de sorte que la fonction de production C-D est

Q=AL3/4 C1/4

qui montre des rendements d’échelle constants car le total des valeurs de L et С est égal à un: ( 3/4 + 1/4), c’est-à-dire (a + β = 1). Le coefficient d’ouvrier dans la fonction C-D mesure l’augmentation en pourcentage de (Q qui résulterait d’une augmentation de 1% de L, tout en maintenant С constant.

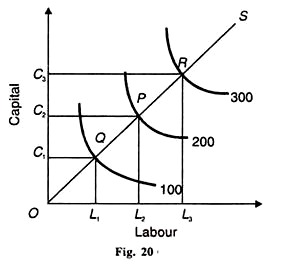
De même, В est le pourcentage d’augmentation de Q qui résulterait d’une augmentation de 1% de C, tout en maintenant L constant. La fonction de production C-D montrant des rendements constants à l’échelle est illustrée à la figure 20. L’apport en main-d’œuvre est pris sur l’axe horizontal et le capital sur l’axe vertical.

Pour produire 100 unités de production, on utilise les unités ОС, les unités de capital et les unités OL de travail. Si la production devait être doublée pour atteindre 200, les intrants de main-d’œuvre et de capital devraient être doublés. ОС est exactement le double de ОС1 et de OL2 est le double de OL2.

De même, si la production doit être multipliée par trois à 300, les unités de travail et de capital devront être multipliées par trois. OC3 et OL3 sont trois fois plus grands que ОС1 et OL1, respectivement. Une autre méthode consiste à prendre la ligne d’échelle ou le chemin d’expansion reliant les points d’équilibre Q, P et R. OS est la ligne d’échelle ou le chemin d’expansion reliant ces points.

Il montre que les isoquantes 100, 200 et 300 sont équidistantes. Ainsi, sur la ligne d’échelle OS OQ = QP = PR qui montre que lorsque le capital et le travail sont augmentés dans des proportions égales, la production augmente également dans la même proportion.

Critiques de la fonction de production C-D:

La fonction de production C-D a été critiquée par Arrow, Chenery, Minhas et Solow comme indiqué ci-dessous :

1. La fonction de production C-D ne considère que deux intrants, le travail et le capital, et néglige certains intrants importants, comme les matières premières, qui sont utilisés dans la production. Il n’est donc pas possible de généraliser cette fonction à plus de deux entrées.

2. Dans la fonction de production C-D, le problème de la mesure du capital se pose car il ne prend que la quantité de capital disponible pour la production. Mais la pleine utilisation du capital disponible ne peut être faite qu’en période de plein emploi. C’est irréaliste car aucune économie n’est toujours à plein emploi.

3. La fonction de production C-D est critiquée car elle montre des rendements d’échelle constants. Mais les rendements constants à l’échelle ne sont pas une réalité, car les rendements croissants ou décroissants à l’échelle sont applicables à la production.

Il n’est pas possible de modifier tous les intrants pour apporter un changement proportionnel dans les extrants de toutes les industries. Certains intrants sont rares et ne peuvent pas être augmentés dans la même proportion que les intrants abondants. D’autre part, les intrants comme les machines, l’entrepreneuriat, etc. sont indivisibles. À mesure que la production augmente en raison de l’utilisation de facteurs indivisibles à leur capacité maximale, le coût unitaire diminue.

Ainsi, lorsque l’offre d’intrants est rare et que des indivisibilités sont présentes, des retours constants à l’échelle ne sont pas possibles. Chaque fois que les unités de différents intrants sont augmentées dans le processus de production, les économies d’échelle et la spécialisation entraînent des rendements d’échelle croissants.

Dans la pratique, cependant, aucun entrepreneur n’aimera augmenter les différentes unités d’intrants afin d’avoir une augmentation proportionnelle de la production. Son objectif est d’obtenir une augmentation plus que proportionnée de la production, bien que des rendements d’échelle plus faibles ne soient pas non plus exclus.

4. La fonction de production C-D est basée sur l’hypothèse de la substituabilité des facteurs et néglige la complémentarité des facteurs.

5. Cette fonction repose sur l’hypothèse d’une concurrence parfaite sur le marché des facteurs, ce qui est irréaliste. Cependant, si cette hypothèse est abandonnée, les coefficients α et β ne représentent pas de parts de facteur.

6. L’une des faiblesses de la fonction C-D est le problème d’agrégation. Ce problème se pose lorsque cette fonction est appliquée à chaque entreprise d’une industrie et à l’ensemble de l’industrie. Dans cette situation, il y aura de nombreuses fonctions de production d’agrégation faible ou élevée. Ainsi, la fonction C-D ne mesure pas ce qu’elle vise à mesurer.

Conclusion:

Ainsi, la praticabilité de la fonction de production C-D dans l’industrie manufacturière est une proposition douteuse. Ceci n’est pas applicable à l’agriculture où, pour la culture intensive, l’augmentation des quantités d’intrants n’augmentera pas proportionnellement la production. Même dans ce cas, on ne peut nier que le retour constant à l’échelle est une étape de la vie d’une entreprise, d’une industrie ou d’une économie. C’est une autre chose que cette étape puisse survenir après un certain temps et pendant un court moment.

C’est important:

Malgré ces critiques, la fonction C-D est d’une grande importance.

1. Il a été largement utilisé dans les études empiriques des industries manufacturières et dans les comparaisons inter-industries.

2. Il est utilisé pour déterminer les parts relatives du travail et du capital dans la production totale.

3. Il est utilisé pour prouver le théorème d’Euler.

4. Ses paramètres a et b représentent des coefficients d’élasticité utilisés pour des comparaisons intersectorielles.

5. Cette fonction de production est linéaire homogène de degré un qui montre des rendements constants à l’échelle, Si α + β = 1, il y a des rendements croissants à l’échelle et si α + β < 1, il y a des rendements décroissants à l’échelle.

6. Les économistes ont étendu cette fonction de production à plus de deux variables.