Un tenseur est un tableau de données (nombres, fonctions, etc.) qui est étendu en un nombre quelconque (0 et plus) de dimensions. Le nombre de dimensions est appelé rang de tenseur.

Tenseur de rang 0

Un tenseur qui n’a pas de dimensions (0).

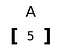
Tenseur de rang 1

Un tenseur développé dans une seule dimension.

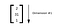
Rank 2 tensor

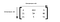
Rank 3 tensor

As shown in figure, a rank 3 tensor has a cube (or cuboid like structure).

If rank of a tensor exceeds 3, it becomes difficult to visualize.

Scalaire

Un scalaire est un tenseur de rang 0. En physique, diverses grandeurs sont représentées sous forme de scalaire telles que: Distance (500 km), Température (10ºC), Vitesse (34 km/h), etc.

Vecteur

Un tenseur de rang 1 est appelé vecteur. Des grandeurs physiques telles que la Vitesse (10 m/s), le Déplacement (54 m vers l’Est), le Champ électromagnétique (1 V/m).

Différence entre scalaire et vecteur :

Une quantité qui ne nécessite pas d’informations supplémentaires (telles que la direction) avec elle (comme la température) est représentée comme scalaire. Alors qu’une quantité dont la direction doit être spécifiée à côté de sa grandeur est représentée par un vecteur (comme le champ électrique).

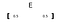
Un vecteur est indiqué avec une lettre en gras (comme « E”) ou une flèche au-dessus de la lettre.

Pour tracer un vecteur, nous utilisons ses éléments comme valeur de coordonnées (axes x, y et z respectivement). Ici, le premier élément (0,5) est pris comme valeur x et le deuxième élément (également, 0,5) est pris comme valeur y (si nous avions trois éléments, le troisième aurait été la valeur z).

Après avoir tracé le vecteur en tant que point, nous y mettons une flèche, d’origine (0,0).

Un vecteur est simplement une matrice qui a soit une ligne (appelée vecteur colonne), soit une colonne (appelée vecteur ligne).

Matrice

Une matrice est un tenseur de rang 2. Nous avons examiné matrix plus tôt.

Un tenseur de rang supérieur à 2 est simplement appelé « tenseur » (il n’y a pas de nom spécifique pour les tenseurs de rang supérieur à 2).

Le concept de tenseur généralise les matrices, les vecteurs et les scalaires sous un même toit (ils sont tous des tenseurs mais avec des rangs différents).

Matrices en tant que produit de vecteurs :

Lorsque deux vecteurs sont multipliés, ils forment une matrice.

Vector X and Y combined, have 6 elements but their product alone has 9 elements. Ainsi, certaines matrices pourraient être décomposées comme un produit de deux vecteurs.