Test de normalité SPSS Kolmogorov-Smirnov
Un test de normalité alternatif est le test de Shapiro-Wilk.
- Qu’est-ce qu’un test de normalité de Kolmogorov-Smirnov?
- Test SPSS de Kolmogorov-Smirnov à partir de TESTS NPAR
- Test SPSS de Kolmogorov-Smirnov à partir de VARIABLES d’EXAMEN
- Signalant un test de Kolmogorov-Smirnov
- Mauvais résultats dans SPSS?

Qu’est-ce qu’un test de normalité Kolmogorov-Smirnov?
Le test de Kolmogorov-Smirnov examine si les scores
sont susceptibles de suivre une certaine répartition dans une population.Pour éviter toute confusion, il existe 2 tests de Kolmogorov-Smirnov :
- il existe un seul échantillon de test de Kolmogorov-Smirnov pour tester si une variable suit une distribution donnée dans une population. Cette ”distribution donnée » est généralement – pas toujours – la distribution normale, d’où le ”test de normalité de Kolmogorov-Smirnov ».
- il existe également le test de Kolmogorov-Smirnov d’échantillons indépendants (beaucoup moins commun) pour tester si une variable a des distributions identiques dans 2 populations.
En théorie, « Test de Kolmogorov-Smirnov » pourrait faire référence à l’un ou l’autre test (mais se réfère généralement au test de Kolmogorov-Smirnov à un échantillon) et devrait être évité. À propos, les deux tests de Kolmogorov-Smirnov sont présents dans SPSS.
Test de Kolmogorov-Smirnov – Exemple simple
Disons que j’ai une population de 1 000 000 personnes. Je pense que leurs temps de réaction sur une tâche sont parfaitement distribués normalement. J’échantillonne 233 de ces personnes et mesure leurs temps de réaction.
Maintenant, la distribution de fréquence observée de ceux-ci différera probablement un peu – mais pas trop – d’une distribution normale. J’exécute donc un histogramme sur les temps de réaction observés et superpose une distribution normale avec la même moyenne et le même écart-type. Le résultat est montré ci-dessous.
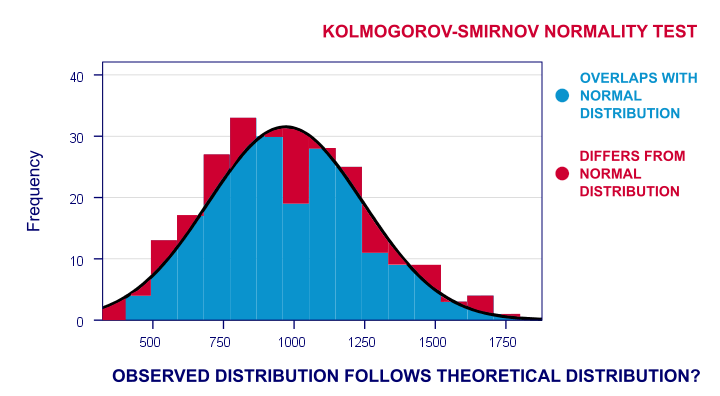
La distribution de fréquence de mes scores ne se chevauche pas entièrement avec ma courbe normale. Maintenant, je pourrais calculer le pourcentage de cas qui s’écartent de la courbe normale – le pourcentage de zones rouges dans le graphique. Ce pourcentage est une statistique de test: il exprime en un seul nombre combien mes données diffèrent de mon hypothèse nulle. Il indique donc dans quelle mesure les scores observés s’écartent d’une distribution normale.
Maintenant, si mon hypothèse nulle est vraie, alors ce pourcentage d’écart devrait probablement être assez faible. Autrement dit, un petit écart a une valeur de probabilité élevée ou une valeur p.
Inversement, un pourcentage d’écart énorme est très peu probable et suggère que mes temps de réaction ne suivent pas une distribution normale dans l’ensemble de la population. Ainsi, un grand écart a une valeur de p faible. En règle générale, werject l’hypothèse nulle si p < 0.05.So si p < 0,05, nous ne croyons pas que notre variable suit une distribution normale dans notre population.
Test de Kolmogorov-Smirnov -Statistique de test
C’est donc le moyen le plus simple de comprendre comment fonctionne le test de normalité de Kolmogorov-Smirnov. Sur le plan informatique, cependant, cela fonctionne différemment: il compare les fréquences relatives cumulatives observées par rapport aux fréquences relatives cumulatives attendues, comme indiqué ci-dessous.
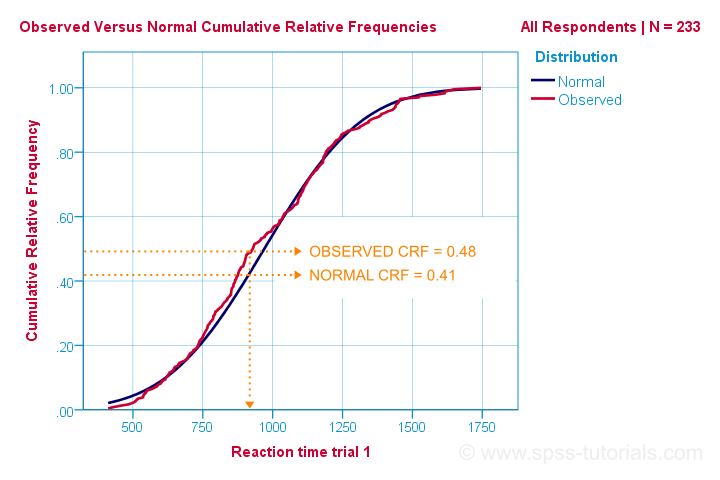
Le test de Kolmogorov-Smirnov utilise la différence absolue maximale entre ces courbes comme statistique de test notée D. Dans ce graphique, la différence absolue maximale D est (0,48-0,41 =) 0,07 et elle se produit à un temps de réaction de 960 millisecondes. Gardez à l’esprit que D = 0,07 comme nous le rencontrerons dans notre sortie SPSS dans une minute.
Le test de Kolmogorov-Smirnov dans SPSS
Il y a 2 façons d’exécuter le test dans SPSS:
- TESTS NPAR trouvés sous Analyser
 Tests non paramétriques
Tests non paramétriques  Boîtes de dialogue héritées
Boîtes de dialogue héritées  1-Sample K-S… est notre méthode de choix car elle crée une sortie bien détaillée.
1-Sample K-S… est notre méthode de choix car elle crée une sortie bien détaillée. - EXAMINER les VARIABLES de l’analyse
 Statistiques descriptives
Statistiques descriptives  Explorer est une alternative. Cette commande exécute à la fois le test de Kolmogorov-Smirnov et le test de normalité de Shapiro-Wilk.
Explorer est une alternative. Cette commande exécute à la fois le test de Kolmogorov-Smirnov et le test de normalité de Shapiro-Wilk.
Notez que EXAMINER les VARIABLES utilise l’exclusion par liste des valeurs manquantes par défaut. Donc, si je teste 5 variables, mes 5 tests ne testent que les cas d’utilisation qui n’ont manqué aucune de ces 5 variables. Ce n’est généralement pas ce que vous voulez, mais nous allons montrer comment éviter cela.
Nous allons démontrer les deux méthodes en utilisant des tâches de vitesse.sav partout, dont une partie est illustrée ci-dessous.
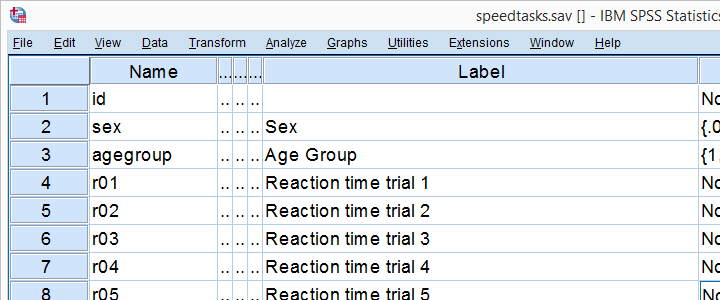
Notre principale question de recherche estquelle des variables de temps de réaction est susceptible d’être normalement distribuée dans notre population?Ces données sont un exemple classique de la raison pour laquelle vous devez inspecter soigneusement vos données avant de commencer à les modifier ou à les analyser. Faisons exactement cela et exécutons quelques histogrammes à partir de la syntaxe ci-dessous.
fréquences r01 à r05
/ format notable
/ histogramme normal.
* Notez que certaines distributions ne semblent pas du tout plausibles!
Résultat
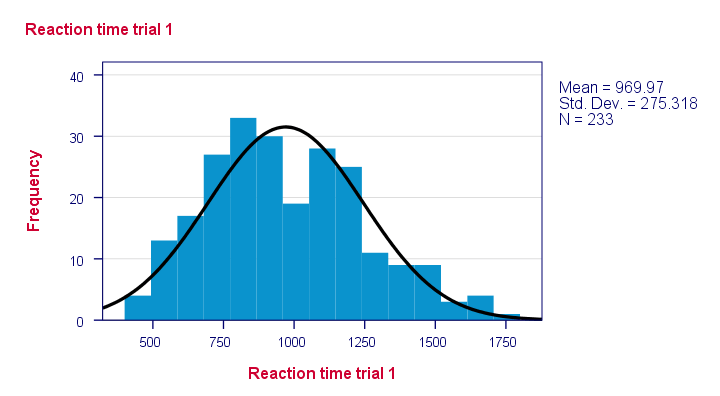
Notez que certaines distributions ne semblent pas plausibles du tout. Mais lesquels sont susceptibles d’être distribués normalement?
Test de Kolmogorov-Smirnov SPSS à partir de TESTS NPAR
Notre option préférée pour exécuter le test de Kolmogorov-Smirnov est underAnalyze  Tests non paramétriques
Tests non paramétriques  Boîtes de dialogue héritées
Boîtes de dialogue héritées  1 – Échantillon K-S… comme indiqué ci-dessous.
1 – Échantillon K-S… comme indiqué ci-dessous.

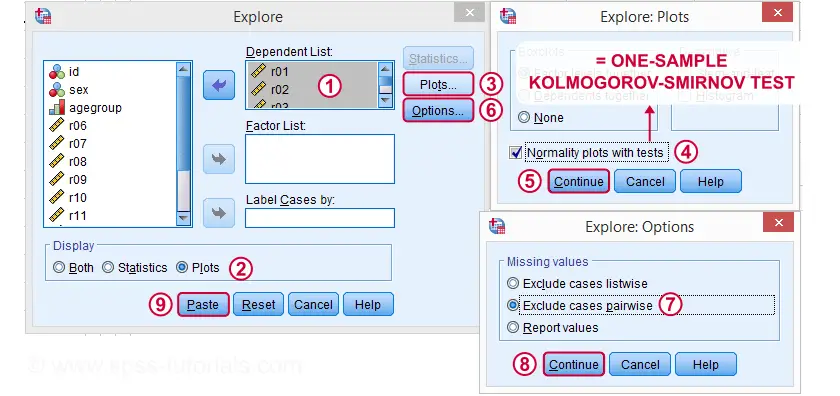
Ensuite, nous remplissons simplement la boîte de dialogue comme indiqué ci-dessous.

En cliquant sur Coller, vous obtenez la syntaxe ci-dessous. Allons-y.
Syntaxe de test de Kolmogorov-Smirnov à partir de Tests Non paramétriques
TESTS NPAR
/ K-S (NORMAL) = r01 r02 r03 r04 r05
/ ANALYSE MANQUANTE.
* Seul le temps de réaction 4 a p> 0,05 et semble donc normalement distribué en population.
Résultats

Tout d’abord, notez que la statistique de test pour notre première variable est de 0,073 – tout comme nous l’avons vu dans notre graphique des fréquences relatives cumulatives un peu plus tôt. Le graphique contient exactement les mêmes données sur lesquelles nous venons d’effectuer notre test, de sorte que ces résultats convergent bien.
En ce qui concerne notre question de recherche: seuls les temps de réaction pour l’essai 4 semblent être normalement distribués.
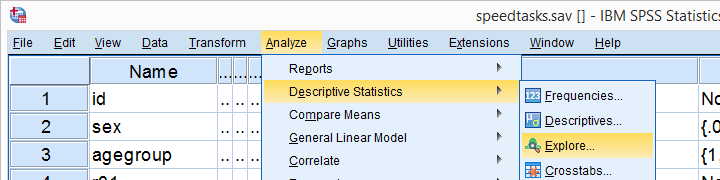
Test de Kolmogorov-Smirnov SPSS à partir d’EXAMINER LES VARIABLES
Une autre façon d’exécuter le test de Kolmogorov-Smirnov commence à partir d’Analyser  Statistiques descriptives
Statistiques descriptives  Exploreras ci-dessous.
Exploreras ci-dessous.
Syntaxe du Test de Kolmogorov-Smirnov à partir de Tests Non paramétriques
EXAMINE VARIABLES=r01 r02 r03 r04 r05
/PLOT BOXPLOT NPPLOT
/COMPARE GROUPS
/STATISTICS NONE
/CINTERVAL 95
/MISSING PAIRWISE /*IMPORTANT!*/
/NOTOTAL.
*Shorter version.
EXAMINE VARIABLES r01 r02 r03 r04 r05
/PLOT NPPLOT
/missing pairwise /*IMPORTANT!*/.
Results
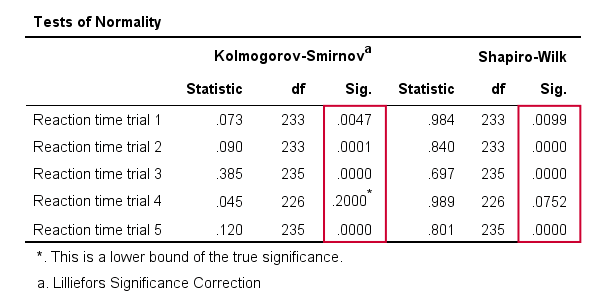
As a rule of thumb, we conclude thata variable is not normally distributed if « Sig.” < 0.05.Ainsi, le test de Kolmogorov-Smirnov ainsi que les résultats du test de Shapiro-Wilk suggèrent que seul le contre-la-montre de réaction 4 suit une distribution normale dans l’ensemble de la population.
En outre, notez que les résultats des tests de Kolmogorov-Smirnov sont identiques à ceux obtenus à partir des TESTS NPAR.
Rapporter un test de Kolmogorov-Smirnov
Pour rapporter nos résultats de test suivant les directives de l’APA, nous écrirons quelque chose comme « un test de Kolmogorov-Smirnov indique que les temps de réaction de l’essai 1 ne suivent pas une distribution normale, D(233) = 0,07, p = 0,005.”Pour les variables supplémentaires, essayez de raccourcir cela, mais assurez-vous d’inclure
- D (pour « différence”), la statistique de test de Kolmogorov-Smirnov,
- df, les degrés de liberté (qui sont égaux à N) et
- p, la signification statistique.

Mauvais résultats dans SPSS?
Si vous êtes un étudiant qui veut juste passer un test, vous pouvez arrêter de lire maintenant. Suivez simplement les étapes dont nous avons discuté jusqu’à présent et vous serez bon.
À droite, maintenant, exécutons exactement les mêmes tests dans la version SPSS 18 et jetons un coup d’œil à la sortie.

Dans cette sortie, les valeurs p exactes sont incluses et, heureusement, elles sont très proches des valeurs p asymptotiques. Moins heureusement, cependant, les résultats de la version 18 du SPSS sont très différents
des résultats de la version 24 du spssnous avons rapporté jusqu’à présent.
La raison semble être la correction de signification de Lilliefors qui est appliquée dans les nouvelles versions de SPSS. Le résultat semble être que les niveaux de signification asymptotique diffèrent beaucoup plus de la signification exacte qu’ils ne le faisaient lorsque la correction n’est pas implicite. Cela soulève de sérieux doutes quant à l’exactitude des « résultats Lilliefors” – la valeur par défaut dans les nouvelles versions SPSS.
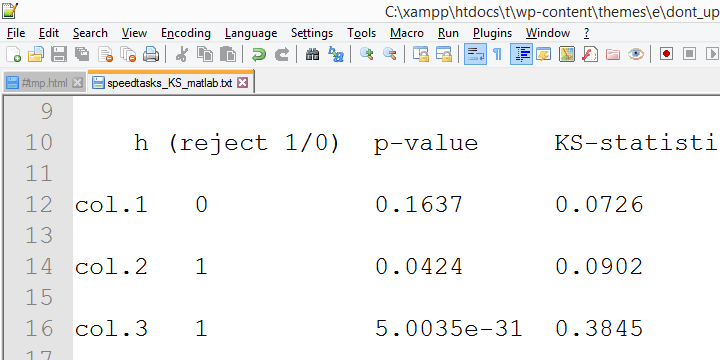
Des preuves convergentes de cette suggestion ont été recueillies par mon collègue Alwin Stegeman qui a réexaminé tous les tests dans Matlab. Les résultats de Matlab sont en accord avec les résultats SPSS 18 et – par conséquent – pas avec les résultats les plus récents.
Test de normalité de Kolmogorov-Smirnov – Utilité limitée
Le test de Kolmogorov-Smirnov sert souvent à tester l’hypothèse de normalité requise par de nombreux tests statistiques tels que ANOVA, le test t et bien d’autres. Cependant, il est presque systématiquement négligé que de tels tests sont robustes contre une violation de cette hypothèse si la taille des échantillons est raisonnable, disons N ≥ 25.La raison sous-jacente en est le théorème de la limite centrale. Par conséquent, les tests de normalité ne sont nécessaires que pour des échantillons de petite taille si l’objectif est de satisfaire l’hypothèse de normalité.
Malheureusement, la petite taille des échantillons entraîne une faible puissance statistique pour les tests de normalité. Cela signifie que des écarts substantiels par rapport à la normalité n’entraîneront pas de signification statistique. Le test dit qu’il n’y a pas d’écart par rapport à la normalité alors qu’il est en fait énorme. En bref, la situation dans laquelle des tests de normalité sont nécessaires – de petites tailles d’échantillons – est également la situation dans laquelle ils fonctionnent mal.
Merci d’avoir lu.
Leave a Reply