節減は、すべてのものが等しいことを示唆する指針であり、現象の最も簡単な説明または問題の最も簡単な解決策を好むべきである。 たとえば、家の中から吠え声が聞こえ、犬を所有している場合、他の犬がこっそり入っていると仮定するよりも、今自分の犬を聞いていると仮定する方が合理的です。節約は、さまざまなシナリオであなたの推論と意思決定を導くのに役立つ便利な概念です。

節約は、あなたの推論と意思決定を導くのに役立ちま そのため、次の記事では節減についての詳細を学び、節減の使用方法の例を見て、節減に関するいくつかの重要な注意点を理解し、できるだけ効果的に

節減の理解

“一般的には、このような手順に大きな異議を提供する観測には何もない限り、可能な限り最も単純な仮説によって現象を説明することは良い原則であると考えています。”

—天文学者プトレマイオス（紀元前150年頃）による”アルマゲスト”から。 この引用は、2001年の著書”The Science of Conjecture:Evidence and Probability before Pascal”の学者James Franklinによって特定されました。

節約の概念は、利用可能なオプションの複雑さに基づいて、現象の最も合理的な説明や問題に対する最良の解決策を特定するのに役立 具体的には、節約の原則によれば、最良の説明や解決策を探すときは、利用可能なオプションを選択するために他の基準を使用できない限り、最も簡単

与えられた説明や解の複雑さは、文脈や関係する要因に基づいて、多くの方法で定義することができます。

与えられた説明や解の複雑さは、多くの方法で定義することができます。 しかし、一般的には、複雑さは、与えられた説明が意味をなすために必要とされる仮定の数に基づいており、最も単純な説明（すなわち、最も節約的な説明）は、最も少ない仮定を必要とするものである。

さらに、節減的な説明はより簡単であるため、幅広い状況でより一般化する傾向があります。 これは、倹約的な説明は、手元の状況に固有の多くの仮定に依存しないので、倹約的な説明は、一般的に、より少ない倹約的なものよりも広い範囲の現象を説明することができることを意味する。

これにより、人々は倹約的な説明と解決策を好ましいだけでなく、より”エレガント”であると見なすようになりました。 たとえば、コードについて言えば、Doug McIlroyとJon Bentleyは次のように述べていると報告されています。

“パフォーマンスの鍵は優雅さであり、特別なケースの大隊ではありません。”

これは、手元の状況に特別に調整する必要があるものとは対照的に、きれいで一般化可能な説明や解決策の好みを示しています。

注：この方法での節減の使用は、節減の原則または節減の法則と呼ばれることがあります。 単語の哲学的および科学的な使用の外で、’節約’は資源を使うことを好まないことの質として定義される。

節減の例

節減の視覚的な例

次の図を考えてみましょう。

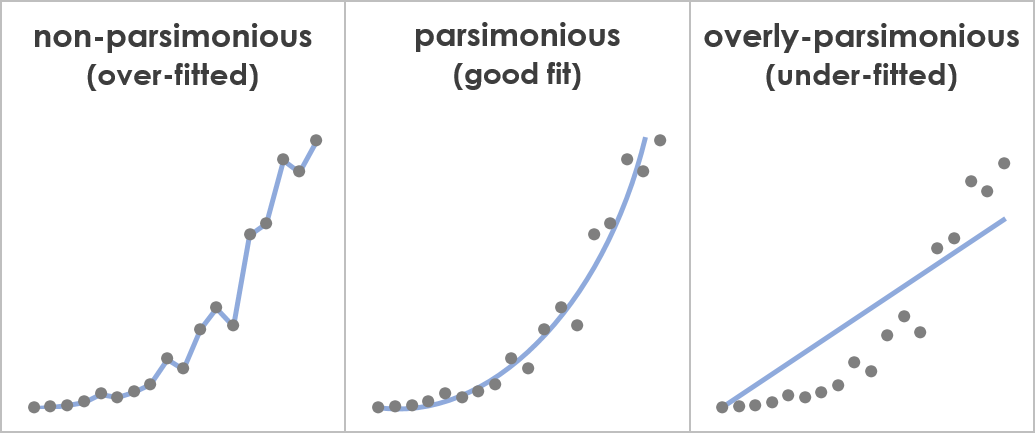
最初のグラフ（左側）は、節度のない説明の例です。 この説明は、この特定の状況で収集された特定のデータポイントに過度に適合しています。

第二のグラフ（中央）は、適切な、倹約的な説明の例です。 この説明は、これらの特定のデータポイントの原因となる根本的な現象を一般化可能な方法で正確に捉えています。

3番目のグラフ（右側）は、過度に節約された説明の例です。 この説明は不十分であり、それは根本的な現象を正確に捉えることができないほど簡単であることを意味します。

全体的に、この例は、一般化可能な方法で手元の現象を正確に捉える倹約的な説明を選択することの重要性を示しています。 このような説明は、特定のデータに過度に適合しているため、根本的な現象を正確に捉えることができない非節約的な説明とは対照的であり、過度に節約的な説明は、根本的な現象を適切に捉えることができないほど単純化されている。

日常生活における節約の例

次のシナリオを考えてみましょう：あなたはあなたの寝室にいて、眠りにつく準備をしています。 さて、スイッチを押した直後にライトが消えた理由については、いくつかの可能な説明があります。

• スイッチを押したためにライトが消えました。
• あなたが光のスイッチを押した瞬間に停電があったので、ライトが消えました。
• ライトスイッチが機能しないので、ライトは実際には消えていませんが、スイッチを押した瞬間に特別なタイプの視力障害が発生し、それが原因

これらの説明は、節減の原則が非常に重要である主な理由の一つを示しています：存在するすべての現象について、無限の数の誤った説明を生成す

一般的にアドホック仮説と呼ばれるこれらの説明は、テストが困難でコストがかかることが多いため、節減の原則は、観察する現象のより合理的な説明を支持してそれらを拒否するために使用できる強力なツールです。さらに、場合によっては、これらの仮説を改ざんすることが困難または不可能である可能性があります。

さらに、これらの仮説は、偽造が困難 たとえば、それはあなたがそれをオフにしようとする試みで光スイッチをクリックするたびに、あなたの部屋に住んでいる検出不可能な外国人は、彼らが最初にあなたの部屋に移動したときに光スイッチを無効にした後、電球の周りに闇のフィールドを撮影することを仮定することが可能です。これはばかげて聞こえるが、人々は歴史の中で同様にばかげたことを信じることが知られていることに注意してください。

これが節約が非常に重要な理由です: あなたがこの説明が間違っていることを示唆する説得力のある証拠を持っていない限り、それはあなたが最も簡単で最も合理的な説明に固執する

この場合、これは、ライトスイッチをクリックしたときにライトがオフになった場合、選択する最も合理的な説明は、スイッチが正常に機能してい この説明が間違っている可能性があることを示唆するさらなる証拠を見つけた場合は、最初の仮説を再検討し、それに応じて修正する必要がありま それ以外の場合は、しかし、それは受け入れるのが最も合理的な説明だから、あなたはそれに固執する必要があります。

科学における節約の例

節約の概念は、多くの場合、より節約の説明が一般的に好まれている科学研究において役割を果たしています。

例えば、個体や種などの生物学的実体間の進化的関係を調べる系統学の分野では、最大節減の原則は、問題の実体間の関係を表す可能性のある系統樹がどれだけうまく表現されているかを評価するために使用されることが多い。

具体的には、この基準の下では、好ましいツリーは、進化的変化の最小数を含むことにより、最も単純であり、したがって最も節約されるツリーである。 例えば、二つの可能な木が与えられ、そのうちの一つは5つの進化的変化を含み、そのうちの一つは6つの進化的変化を含み、二つの別々のケースで独立して発達する特定の形質の結果として追加された変化が起こると、逆を指摘する追加の証拠がない限り、より単純な木が一般的に好まれる。

節減とオッカムの剃刀

節減の原則は歴史を通して多くの定式化で提案されていましたが、オッカムの哲学者ウィリアムによって提案されたオッカムの剃刀によって最も頻繁に操作化されています。簡単に言えば、Occamのrazorは、その説明が他の基準に基づいて他の可能な説明と等しい場合、現象の最も簡単な説明を好むべきであることを示唆しています。このように、Occamの剃刀は哲学的な剃刀であり、現象の最も可能性の高い説明を見つけるのに役立つ指針として役立つことを意味しています。

それは本質的に節減の原則の最も一般的な使用を表していますが、節減は、問題に対する最良の解決策を見つけようとするときなど、現象に対する最良の説明を見つけようとすることを超えた他の状況での指針となる原則としても役立ちます。

節約に関する重要な注意

節約は正しい解決策を保証するものではありません

節約の原則は、オブザーバーが論理的推論に基づいて、特定の拉致推論は、論理的に確実な結論につながる推論の一形態である演繹推論とは対照的である。

拉致推論は、推論の一形態である演繹推論と対比される。

拉致推論は、推論の一形態である。 節減の使用は、あなたが知っていることに基づいて現象の最も合理的な説明に向かってあなたを導くことを意図しているが、必ずしも正しいものに向かっているわけではないので、この区別は心に留めておくことが重要です。例えば、医学では、診断的節約は、一般に、患者が複数の症状を示している場合、それらの症状は単一の病状に起因するべきであると仮定するように医師 しかし、この仮定は、ヒッカムの格言に記載されているように、いくつかの状況では誤っている可能性があり、これは”患者は、彼らが気にしているだけ多くの病気を持つことができる”という格言である。

診断医学の分野でこの概念を説明するもう一つの例は、”蹄を聞くときは、シマウマではなく馬を考える”というゼブラの原則です。 この原則は、患者の症状が比較的一般的な病状（馬で表される）または比較的まれな状態（シマウマで表される）のいずれかに等しく適合する場合、診断医は、患者がより一般的な状態に苦しんでいると仮定すべきであることを示している。 しかし、この原則は、患者が必ずしもより一般的な状態に苦しむことを保証するものではなく、むしろそれ以外のことを示唆する証拠がない場合、それは単に彼らがこの状態ではなく、よりまれなものに苦しむ可能性が高いことを示唆している。全体的に、シンプルでエレガントな理論は一般的に好ましいが、それは必ずしも正しいという意味ではない。

そのため、節減は、現象の最も合理的な説明を見つけるのに役立つ有用な指針であるにもかかわらず、その説明が正しいかどうかを判断するのに役立節約の原則を適用すると、最も単純な説明や解決策が必然的に最良のものであると仮定すると、人々は時には過度に熱心になります。

節約の原則を適用すると、最も単純な説明や解決策が必然的に最良のものであると仮定すると、人々は時には節約の原則を適用すると、人々は時には節約の原則を適用すると、人々は時には節約の原則を適用すると、 ただし、節約は、一般的に、いくつかのオプションのどれが最適かを選択するのに役立つ基準の1つだけとして機能することを意図しています。たとえば、コードを記述し、いくつかの可能なアプローチの間で決定しようとしている場合、節減は確かに考慮すべき要因ですが、それだけではありません。 可読性、効率性、有効性などの他の要因も考慮する必要があります。

このような要因は、多くの場合、節減と相関しているが、この相関はめったに完璧ではなく、それはあなたの好みのアプローチを選ぶことになると、こ たとえば、より複雑なオプションが意図した結果を達成することができれば、複雑なコードをより単純なものよりも選択することができます。節約を過度に適用すべきではないという考えは、歴史を通して様々な哲学者や科学者によって異なる定式化で示唆されてきました。

これらの定式化の中で最も有名なのは、チャットンの原理を提案した哲学者ウォルター-オブ-チャットンによって提案されました。

“三つのことが物事についての肯定的な命題を検証するのに十分でない場合は、四番目を追加する必要があります。”

彼は後にこれを次の定式化に拡張しました:

“肯定的な命題が実際に存在するものに対して検証される傾向があるときはいつでも、二つのものが配置と期間に応じて存在する方法であれば、別のものが欠けている間に命題の検証に十分ではない場合は、その他のものを仮定しなければならない。”

同様に、哲学者エマニュエル-カントは言った：

“人間の多様性は軽率に減少すべきではありません。”

最後に、有名な物理学者アルバート-アインシュタインは、次のように述べていることが報告されています。

“…すべての理論の最高の目標は、既約な基本要素を、単一の経験データの適切な表現を放棄することなく、できるだけ単純で最小限にすることです。”

また、一般的にアインシュタインに起因する次の引用は、時々アインシュタインの剃刀と呼ばれるこの概念を、より簡潔に伝えます:P>

“物事はできるだけシンプルにする必要がありますが、単純ではありません。”

注：上記の概念のいくつかは、よく知られているオッカムのかみそりと矛盾すると考えられているため、アンチかみそりまたはカウンターかみそりと呼ばれることがありますが、少なくともある程度は実際にはそれを洗練するだけです。 しかし、これらの概念は、観察者が遭遇する現象の最も可能性の高い説明を見つけるのを助けるための論理的なツールであるため、まだ一般的には哲学的なカミソリであると考えられている。節減の概念は、現象の説明や問題の解決策を見つけようとしている状況で、実装するのに便利なツールになります。上記のセクションでは、節減とは何か、なぜそれが重要なのか、それを実装するときに注意する必要があることを示しています。 簡潔に述べると、節減の原則を実装することは、より複雑なオプションを選択する説得力のある理由がない限り、より複雑なものよりも簡単な説明と解

これは、この原則を実装するときは、まず関連する基準に基づいてすべての可能なオプションを評価し、最良のものを見つけようとする必要があ 次に、必要に応じて、最も単純で最も一般化可能な説明または解決策を選択することで、これらのトップ少数のオプションの中から選択するのに役立

しかし、いくつかの利用可能なオプションの間で選択するための基準として節約を使用するときは、常に警戒することを覚えておいて、節約は、あなたが使用すべきいくつかの基準の一つに過ぎず、最も節約的な説明が正しいものであることが保証されていないことに注意してください。

要約と結論

• 節減は、すべてのものが等しいことを示唆する指針であり、現象の最も簡単な説明または問題の最も簡単な解決策を好む
• たとえば、家の中から吠え声が聞こえ、犬を所有している場合、他の犬がこっそり入っていると仮定するよりも、今自分の犬を聞いていると仮定す
• 倹約的な説明や解決策は、一般的に最小限の仮定を必要とするものであり、多くの特定の警告を必要とせずにlarges範囲のコンテキストで動作するために一般化することができるため、より”エレガント”と見なされることが多い。
• 節減の原則を実装するとき、それはシンプルさは、あなたが利用可能な説明や解決策から選択するために使用できるいくつかの可能な基準の一つに過ぎないことを覚えておくことが重要です。
• さらに、節減の原則を実装するときは、この原則は、あなたが持っている情報を与えられた現象の最も合理的な説明を見つけるのに役立ちますが、そ