以下の記事では、Cobb-Douglas Production Functionについての詳細なビューを提供しています。

Cobb-Douglas生産関数は、Paul H.DouglasとC.W.Cobbによって行われたアメリカの製造業の実証的研究に基づいています。 これは、の出力全体に対して、2つの入力、労働と資本を考慮に入れた次数1の線形均質生産関数です。製造業。

Cobb-Douglas生産関数は次のように表されます:

Q=ALa Cß

ここで、Qは出力であり、LとΣはそれぞれ労働と資本の入力です。 A,a,βは正のパラメータであり、=a>O,β>O.

式は、出力がLとCに直接依存し、LとΘで説明できない出力の部分は、多くの場合、技術的な変更と呼ばれる”残差”であるaによって説明されることを示しています。

Cobb-Douglasによって解決された生産関数は、製造業の増加に対する資本の1/4の貢献と労働の3/4を持っていたので、C-D生産関数は

Q=AL3/4C1/4

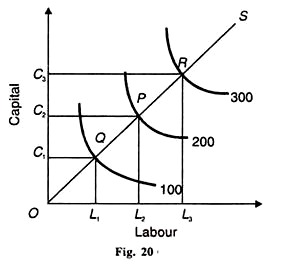
LとΠの値の合計が一つに等しいため、スケールに一定のリターンを示している。（3/4すなわち、（Ａ＋Β＝１）である。 C-D関数の労働者係数は、Λを定数として保持しながら、Lの1パーセントの増加に起因する（Q）の増加率を測定します。 同様に、Λは、Lを一定に保持しながら、Cの1％の増加に起因するQの増加率です。 定数がスケールに戻ることを示すC-D生産関数を図20に示します。 労働投入は水平軸に、資本は垂直軸に取られます。

100単位の出力を生成するには、ОС、資本単位、ol単位の労働単位が使用されます。 生産量を200に倍増させるには、労働と資本の投入量を2倍にする必要があります。 Σはσ1の正確な二重であり、ol2はol2の二重です。

同様に、出力を300に三倍に上げる場合は、労働と資本の単位を三倍に増やす必要があります。 OC3およびOL3は、それぞれΣ1およびol1の三倍大きい。 別の方法は、平衡点Q、PおよびRを結ぶスケール線または拡張経路を取ることである。OSは、これらの点を結ぶスケール線または拡張経路である。 これは、等量100、200、および300が等距離であることを示しています。

したがって、OSスケールラインOQ=QP=PRこれは、資本と労働が等しい割合で増加すると、出力も同じ割合で増加することを示しています。

C-D生産関数の批判：

C-D生産関数は、以下で説明するようにArrow、Chenery、Minhas、Solowによって批判されています。

1. C-D生産機能は、労働と資本の二つの入力のみを考慮し、生産に使用される原材料のようないくつかの重要な入力を無視します。 したがって、この関数を2つ以上の入力に一般化することはできません。

2. C-D生産機能では、生産に利用可能な資本の量だけを取るため、資本の測定の問題が発生します。 しかし、利用可能な資本を最大限に活用することは、完全雇用期間中にのみ行うことができます。 経済は常に完全に採用されていないので、これは非現実的です。 p>

3. C-D生産関数は、スケールへの一定の戻り値を示すため、批判されています。 しかし、スケールへの一定のリターンは、スケールへのリターンの増加または減少のいずれかが生産に適用可能であるため、現実ではありません。 すべての産業の出力に比例した変化をもたらすためにすべての入力を変更することはできません。

すべての入力を変更することはできません。

いくつかの入力は不足しており、豊富な入力と同じ割合で増加することはできません。 一方で、入力は機械、企業家精神、等のような。 不可分である。 最大容量に不可分な要因を使用することにより出力が増加するにつれて、単位コストごとに低下する。 p>

したがって、入力の供給が不足し、独立性が存在する場合、定数がスケールに戻ることはできません。 異なる入力の単位が生産プロセスで増加するたびに、規模と専門化の経済は、スケールへのリターンを増加させることにつながります。 しかし、実際には、起業家は、生産量を比例的に増加させるために、さまざまな入力単位を増やすことを望んでいません。

しかし、実際には、起業家は、生産量を比例的に増加させることを望んでいません。 彼の努力は、生産量の比例した増加以上のものを持つことですが、規模へのリターンの減少も除外されていません。

4. Ｃ-Ｄ生産関数は因子の置換可能性の仮定に基づいており，因子の相補性を無視している。

5. この機能は非現実的である要因市場の完全な競争の仮定に基づいている。 ただし、この仮定が省略された場合、係数αおよびβは因子共有を表しません。

6. C-D関数の弱点の1つは集約問題です。 この問題は、この機能が業界内のすべての企業と業界全体に適用される場合に発生します。 このような状況では、低または高集約の多くの生産関数が存在します。 したがって、C-D関数は、それが測定を目的とするものを測定しません。

結論：

したがって、製造業におけるC-D生産機能の実用性は疑わしい命題である。

結論：

結論：

結論：

これは集中的な耕作のために、量の入力を高めることが生産を比例して上げない農業に適当ではない。 それでも、一定の規模への復帰は、企業、産業、経済の生活の段階であることを否定することはできません。 この段階はしばらくしてから、しばらくの間来るかもしれないということもあります。

それは重要です：

これらの批判にもかかわらず、C-D関数は非常に重要です。

1. これは、製造業の実証研究や業界間の比較で広く使用されてきました。

2. これは、総生産における労働と資本の相対的なシェアを決定するために使用されます。

3. これはオイラーの定理を証明するために使用されます。

4. そのパラメータaとbは、部門間の比較に使用される弾性係数を表します。

5. この生成関数は次数1の線形同次であり、α+β=1の場合、スケールへの戻り値が増加し、α+β<1の場合、スケールへの戻り値が減少します。

6. 経済学者は、この生産関数を2つ以上の変数に拡張しました。p>