일반적인 표기법의 기능은 일반적으로 기록으로,

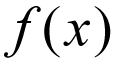
지 않는 생각도 말 그대로,즉,f 는 곱하 x. 대 으로 이것을 고려하는 수학적 표현으로 읽

또는

기능을 작성할 수도 있습니다 다른 방법으로 사용하여 다른 변수와 같이

• g(x),h(x),k(x)

또한,함수에 걸릴 수 있습니다 다른 입력 값 이외의 다른 x.

• f(a),h(r),k(m)

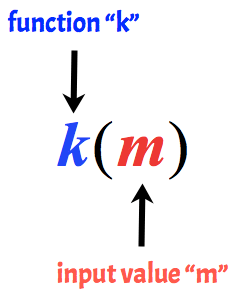
중요한 아이디어는 항상 기억하는 변수를 괄호 밖에는”이름”의 기능을하는 동안,이 변수는 괄호 안에 입력합니다.

예를 들어,다음과 같은 함수 호출에 k 으로 입력 값의 m.

기본적인 예의 평가 기

예제 1:을 평가하는 기능입니다.

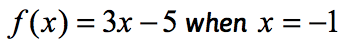
이것은 정상적인 표기법의 기능 함수가 f 는 동안 입력 값입니다. 을 평가하는 기능을,우리가 무엇을 원하는 대용품의 모든 인스턴스에 있는 x 표현한 다음 단순화 할 수 있습니다.

X=-1 이므로 함수에서이 값을 대체하고 단순화합니다. 그렇게함으로써 우리는 다음과 같이 보이는 해결책을 얻습니다.

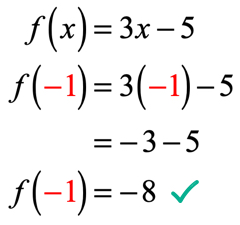
예제 2:함수를 평가하십시오.

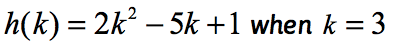
을 관찰하는 기능 여기에서 그리고 입력값이 k. 이전 예제에서와 마찬가지로 k 에 할당 된 숫자 값이 무엇이든 주어진 함수로 대체하고 단순화하려고합니다.

이후 k=3 솔루션은 다음과 같이 나타나야 합니다.

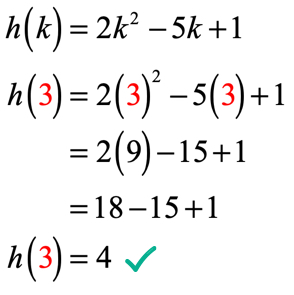
예제 3:아래 함수를 사용하여 아래 표에서 x 의 각 값을 평가하십시오. Xy 축의 점을 플롯하고 점을 연결하여 함수의 그래프를 나타냅니다.

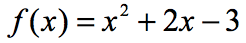
있기 때문에 일곱 x-입력,즉 우리가 기능을 평가 하는 일곱 번뿐만 아니라. 자신에 이것을 밖으로 작동 하려고 다음 다시 귀하의 답변을 확인 하 고.

당신이 그것을 올바르게 수행했다면,이것들은 값들입니다:

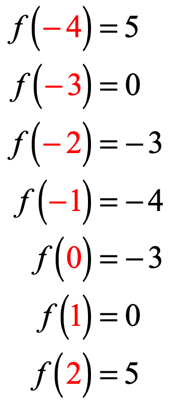
이제 해당 출력 값을 테이블에 배치 할 수 있습니다.

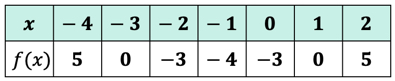
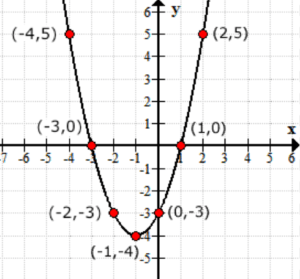
생각하는 값을 출력하는 함수의 f\left(x\오른쪽)이 y 값이다. 이것은 그래프가 xy 축에서 어떻게 보이는지입니다.

함수 평가의 중간 예

예 4:G\left(x\right)={x^2}-3x+1 이 주어지면 g\left({2x-1}\right)를 찾으십시오.

앞의 예에서,우리는 숫자로 함수를 평가하고있다. 이번에는 입력 값이 더 이상 고정 된 숫자 값이 아니라 대신 표현식입니다. 복잡해 보일 수도 있지만 절차는 동일하게 유지됩니다.

우리는 g\left(x\right)에있는 x 의 모든 인스턴스를 2x-1 인 입력 값으로 대체 할 것입니다. 이항식을 제곱하고 분배 속성을 적용하고 용어처럼 결합하여 단순화하십시오.

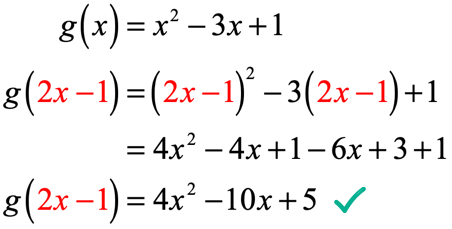
예 5:는 p\left(x\오른쪽)={{4x-1}\위 x}평가,p\left(1\오른쪽)-p\left({-1}\right).

문제를 보일 수 있습니다 처음에는 협박하지만,일단 우리가 그것을 분석 및 적용 무엇을 우리는 이미 알고있는 방법에 대해 평가하는 기능이 없는 나쁜!여기서 수행해야 할 작업은 x=1 에서 함수를 평가 한 다음 x=-\,1 에서 평가할 때 함수의 값으로 빼는 것입니다.

값을 대체 할 때와 단순화 프로세스 중에 매우 조심하십시오. 모든 단계에서 조심하지 않으면 양수와 음수를 더하거나 빼거나 곱하거나 나눌 때 실수를 저지르는 것이 매우 쉽습니다.

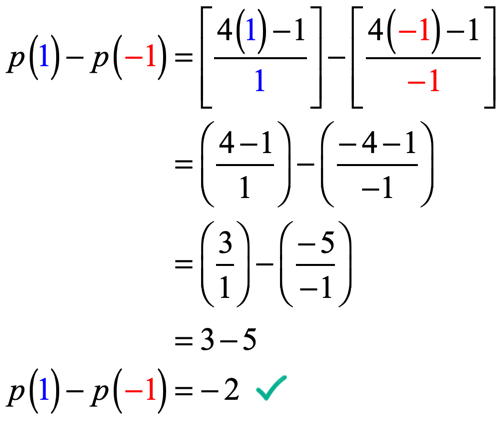
고급 예를 적용하는 개념을 평가하는 기능

예 6:는 경우 f\left(2\오른쪽)=9,값을 찾아의 함수에서 아래.

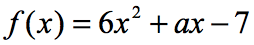
에서 방정식,f\left(2\오른쪽)=9,우리에게는 경우에는 입력의 기능은 2; 함수의 출력은 9 가됩니다. 함수가 우리에게 주어지기 때문에,우리의 첫 번째 움직임은 적어도 2 의 값을 대체 한 다음 단순화하는 것입니다. 이것이 우리가 얻을 것입니다.

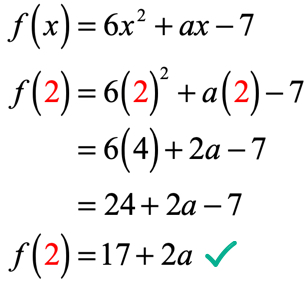
출력의 기능을 평가한 후에서 x=2:17+2a. 기억 우리는 또한 우리가 말하는 출력이 9 를 사용하여 지정된 방정식을 f\left(2\오른쪽)=9. 따라서 우리가 무엇을 할 필요가 지금 설정을 동일하게 서로를 해결합선형 방정식에 대해 알 수 없는 값입니다.

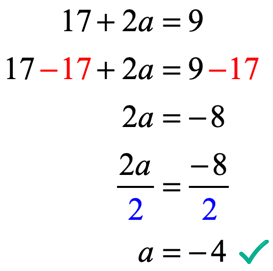
자인 경우의 값=-\,4in f(x)=6{x^2}+ax-7 만들 수 있습이 주어진 조건 f\left(2\오른쪽)=9 진정한 문입니다.

It’s true! 따라서 a 의 올바른 값에 대해 성공적으로 해결했습니다.