대체 정규성 테스트는 Shapiro-Wilk 테스트입니다.

• Kolmogorov-Smirnov 정규성 테스트 란 무엇입니까?
• NPAR 테스트에서 SPSS Kolmogorov-Smirnov 테스트
• 검사 변수에서 SPSS Kolmogorov-Smirnov 테스트
• SPSS 에서 잘못된 결과를보고 있습니까?

Kolmogorov-Smirnov 정규성 테스트 란 무엇입니까?

Kolmogorov-Smirnov 테스트는 점수
이 일부 인구에서 일부 분포를 따를 가능성이 있는지 검사합니다.에 대한 혼란을 피하기 있는 2 개의 Kolmogorov-Smirnov 테스트:

• 있는 하나의 샘플 Kolmogorov-Smirnov 테스트를 테스트하는 경우는 변수는 다음과 같이 특정 분포에는 인구입니다. 이”주어진 분포”는 일반적으로-항상 그런 것은 아니며 정규 분포이므로”Kolmogorov-Smirnov 정규성 테스트”입니다.
• 변수가 2 개의 모집단에서 동일한 분포를 가지고 있는지 테스트하기위한(훨씬 덜 일반적인)독립적 인 샘플 Kolmogorov-Smirnov 테스트도 있습니다.

이론적으로,”Kolmogorov-Smirnov 테스트”를 참조할 수 있을 테스트하고(그러나 일반적으로 하 샘플 Kolmogorov-Smirnov 테스트)와 더 나은 피할 수 있습니다. 그건 그렇고,두 Kolmogorov-Smirnov 테스트는 SPSS 에 있습니다.

Kolmogorov-Smirnov 테스트-간단한 예

그래서 1,000,000 명의 인구가 있다고 가정 해보십시오. 나는 어떤 작업에 대한 그들의 반응 시간이 완벽하게 정상적으로 분산되어 있다고 생각한다. 나는이 사람들 중 233 명을 샘플링하고 반응 시간을 측정합니다.
이제 이들의 관찰 된 주파수 분포는 아마도 정규 분포와 조금 다를 것입니다. 따라서 관찰 된 반응 시간에 걸쳐 히스토그램을 실행하고 동일한 평균 및 표준 편차로 정규 분포를 중첩합니다. 결과는 아래와 같습니다.

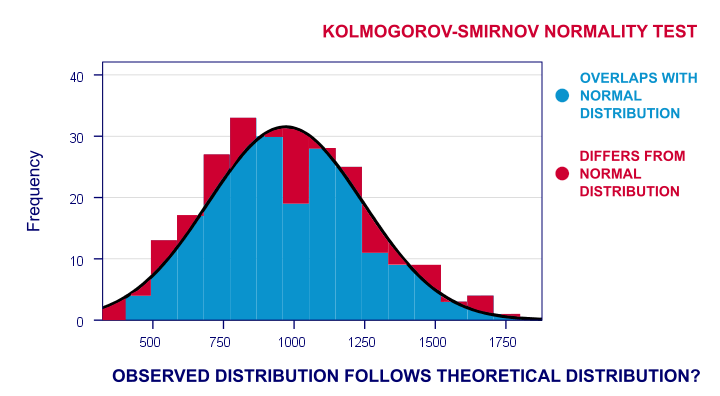
주파수 분포를 나의 점수하지 않는 전적으로 중복으로 나의 정상적인 곡선입니다. 이제 차트에서 빨간색 영역의 비율 인 정상 곡선에서 벗어난 경우의 비율을 계산할 수있었습니다. 이 비율은 테스트 통계입니다:내 데이터가 귀무 가설과 얼마나 다른지를 단일 숫자로 표현합니다. 따라서 관찰 된 점수가 정규 분포에서 어느 정도 벗어나는 지 나타냅니다.
자,내 귀무 가설이 사실이라면,이 편차 비율은 아마도 아주 작아야합니다. 즉,작은 편차는 높은 확률 값 또는 p-값을 갖습니다.
반전으로,거대한 편차는 비율입니다 매우 가능성이 제안하는 나의 반응 시간을 따르지 않는 일반 배포하지 않습니다. 따라서 큰 편차는 낮은 p 값을 갖습니다. 엄지 손가락의 규칙으로,wereject null 가설을 경우에는 p<0.05.그래서 만약 p<0.05,우리는 믿지 않는 변수에 다음과 같은 정상 유통에서 우리의 인구입니다.

Kolmogorov-Smirnov 테스트-테스트 통계

그는 가장 쉬운 방법을 이해하는 방법 Kolmogorov-Smirnov 정규성 검정을 작동합니다. 계산,그러나,그것은 다르게 작동합니다:그것은 비교 관찰 대상이 누적이 상대 주파수로 아래와 같습니다.

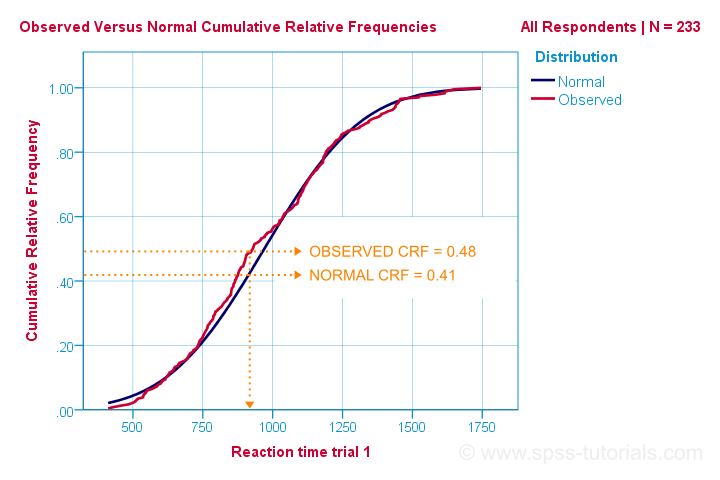
Kolmogorov-Smirnov 테스트를 사용하는 최대 절대 차이는 이 곡선으로 테스트 통계에 의해 표시된 D. 이 차트에서 최대한 절대적인 차이점 D(0.48-0.41=)0.07 및 발생에서 반응 시간 960 밀리초 단위입니다. 우리는 분 안에 우리의 SPSS 출력에서 그것을 만날 것이므로 D=0.07 을 명심하십시오.

SPSS 에서 Kolmogorov-Smirnov 테스트

SPSS 에서 테스트를 실행하는 두 가지 방법이 있습니다:

• NPAR 테스트에서 찾을 분석하는1-샘플 K-S… 멋지게 상세한 출력을 생성하기 때문에 우리의 선택 방법입니다.
• 변수를 조사하는 분석에서탐구하는 대안입니다. 이 명령은 Kolmogorov-Smirnov 테스트와 Shapiro-Wilk 정규성 테스트를 모두 실행합니다.
  검사 변수는 기본적으로 결측 값의 listwise 제외를 사용합니다. 따라서 5 개의 변수를 테스트하면 내 5 개의 테스트는이 5 가지 변수 중 하나에 대한 미싱이없는 사례 만 사용합니다. 이것은 일반적으로 당신이 원하는 것이 아니지만이를 피하는 방법을 보여 드리겠습니다.

speedtasks 를 사용하여 두 가지 방법을 모두 보여 드리겠습니다.sav 는 전체적으로 아래에 나와 있습니다.

우리의 주요 연구문 iswhich 의 반응시간 변수를 가능성이 높
것을 일반적으로는 분산에서의 인구는?이러한 데이터는 편집 또는 분석을 시작하기 전에 데이터를 철저히 검사해야하는 이유에 대한 교과서 예입니다. 그냥하고 아래 구문에서 몇 가지 히스토그램을 실행 해 보겠습니다.

결과

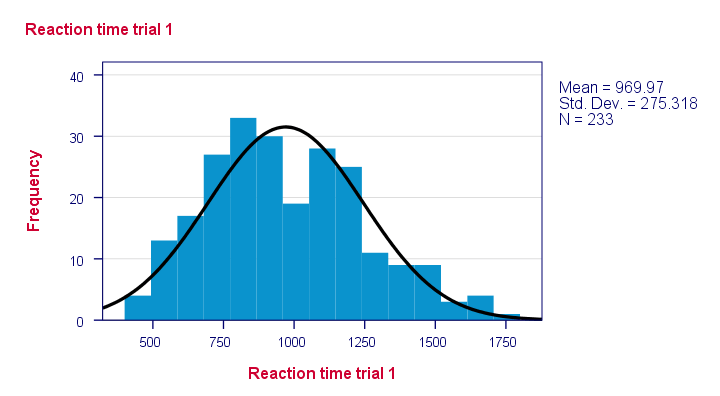
주는 일부 배포하지 않 보면 그럴듯한다. 그러나 어떤 것들이 정상적으로 배포 될 가능성이 있습니까?

SPSS Kolmogorov-Smirnov 테스트에서 NPAR 테스트

우리의 기본 옵션을 실행하기 위한 Kolmogorov-Smirnov 테스트 underAnalyze1-샘플 K-S… 아래 그림과 같이.

다음에,우리는 그냥 대화상으로 아래와 같습니다.

붙여넣기를 클릭하 결과에서 아래 구문. 그것을 실행하자.

Kolmogorov-Smirnov 테스트 비모수 테스트에서 구문

결과

첫째,주는 테스트를 통해 우리의 첫 번째 변수 0.073-처럼 우리는 우리에서 누적된 상대 주파수 차트를 조금 일찍니다. 차트는 우리가 방금 테스트를 실행 한 것과 동일한 데이터를 보유하므로 이러한 결과가 멋지게 수렴됩니다.
우리의 연구 질문에 관해서:시험 4 에 대한 반응 시간 만이 정상적으로 분배 된 것으로 보인다.

SPSS Kolmogorov-Smirnov 테스트에서는 변수를 조사하는

는 다른 방법을 실행하 Kolmogorov-Smirnov 테스트 시작에서 분석하는Exploreas 아래와 같습니다.

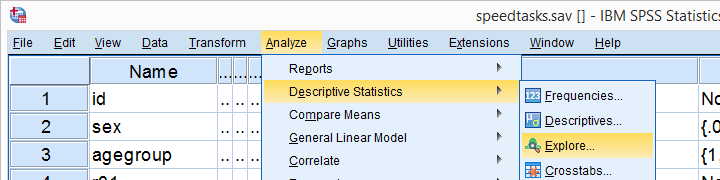
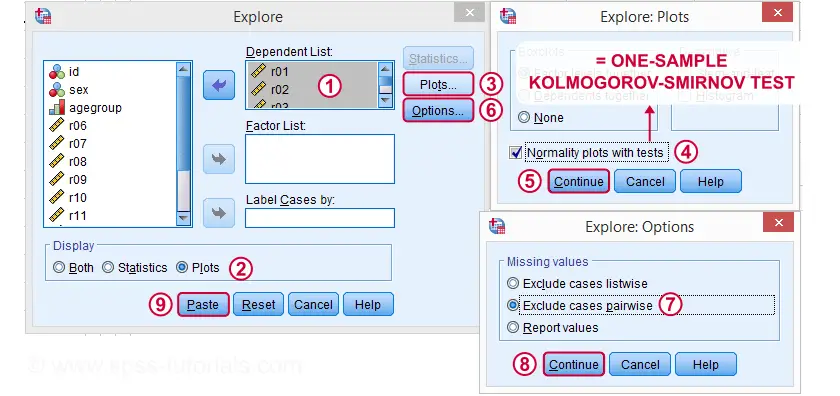
Kolmogorov-Smirnov 테스트는 구문에서 비모수적 테스트

Results

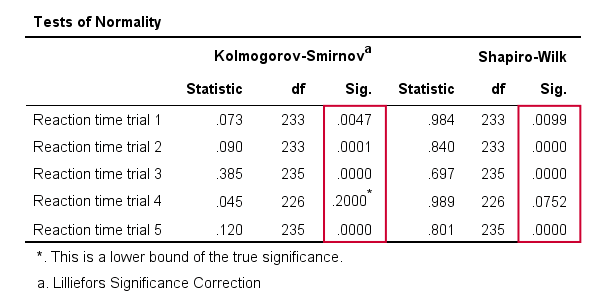
As a rule of thumb, we conclude thata variable is not normally distributed if “Sig.” < 0.05.따라서 Kolmogorov-Smirnov 테스트와 Shapiro-Wilk 테스트 결과는 모두 반응 시간 시험 4 만이 전체 인구에서 정규 분포를 따른다는 것을 암시합니다.
또한,Kolmogorov-Smirnov 시험 결과는 NPAR 시험에서 얻은 것과 동일하다는 점에 유의하십시오.

보고 Kolmogorov-Smirnov 테스트

보고 우리의 테스트 결과는 다음 APA 지침,우리가 뭔가를 쓰기”와 같은 Kolmogorov-Smirnov 테스트는 것을 나타냅 반응 시간에 시험 1 을 따르지 않는 정상적인 분포,D(233)=0.07,p=0.005.”에 대한 추가적인 변수를 시도하고 단축이지만 포함해야 합니다.

• D(에 대한”차이”),the Kolmogorov-Smirnov 테스트 통계,
• df,자유도(과 같 N)그리고
• p,통계적 의미를 갖는다.

Spss 에서 잘못된 결과?

그냥 시험에 합격하려는 학생이라면 지금 독서를 그만 둘 수 있습니다. 우리가 지금까지 논의한 단계를 따르기 만하면 좋을 것입니다.

자,이제 SPSS 버전 18 에서 동일한 테스트를 다시 실행하고 출력을 살펴 보겠습니다.

이 출력에서,정확한 p 값이 포함되어 있고-다행히-그들은 매우 가까운 asymptotic p 값입니다. 덜 다행스럽게도 SPSS 버전 18 결과는 spss 버전 24 결과와 크게 다릅니다.
그 이유는 최신 SPSS 버전에서 적용되는 Lilliefors 중요성 보정 인 것 같습니다. 결과는 점근 적 유의 수준이 교정이 암시되지 않을 때보 다 정확한 유의 수준과 훨씬 더 다른 것으로 보인다. 이것은 최신 SPSS 버전의 기본값 인”Lilliefors 결과”의 정확성과 관련하여 심각한 의문을 제기합니다.
이 제안에 대한 수렴 증거는 Matlab 에서 모든 테스트를 다시 실행 한 동료 Alwin Stegeman 에 의해 수집되었습니다. Matlab 결과는 spss18 결과에 동의하며 새로운 결과는 그렇지 않습니다.

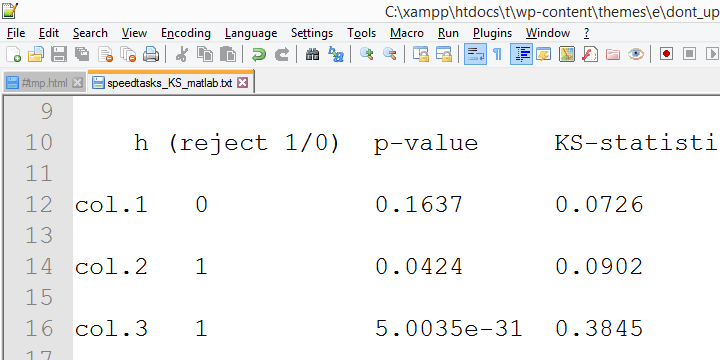
Kolmogorov-Smirnov 정규성 테스트-제한된 유용성

Kolmogorov-Smirnov 테스트를 자주 테스트는 정상의 가정에 필요한 많은 통계적 테스트과 같은 ANOVA,t-테스트하고 많은 다른 사람입니다. 그러나,그것은 거의 정기적으로 간과는 이러한 테스트에 대해 강력한 위반이 가정을 경우 샘플 크기는 합리적인,말 N≥25.이것에 대한 근본적인 이유는 중심 한계 정리입니다. 따라서 정규성 테스트는 작은 샘플 크기에 대해서만 필요합니다.목표는 정규성 가정을 만족시키는 것입니다.
불행히도 표본 크기가 작 으면 정규성 테스트에 대한 통계력이 낮습니다. 이것은 정상 성으로부터의 실질적인 편차가 통계적 유의성을 초래하지 않을 것임을 의미합니다. 이 테스트는 실제로 거대한 동안 정상과의 편차가 없다고 말합니다. 요컨대,정규성 테스트가 필요한 상황-작은 표본 크기-도 제대로 수행되지 않는 상황입니다.

읽어 주셔서 감사합니다.