articolul menționat mai jos oferă o vedere de aproape asupra funcției de producție Cobb-Douglas.

funcția de producție Cobb-Douglas se bazează pe studiul empiric al industriei prelucrătoare americane realizat de Paul H. Douglas și C. W. Cobb. Este o funcție liniară de producție omogenă de gradul unu care ia în considerare două intrări, forța de muncă și capitalul, pentru întreaga producție a .industria prelucrătoare.

funcția de producție Cobb-Douglas este exprimată ca:

Q = ALa C

unde Q este ieșire și l și, respectiv, sunt intrări de forță de muncă și de capital. A, a și XV sunt parametri pozitivi în care = a > O, > O.

ecuația spune că ieșirea depinde direct de L și C, iar acea parte a ieșirii care nu poate fi explicată prin L și la care se explică prin A, care este „reziduală”, adesea numită schimbare tehnică.

funcția de producție rezolvată de Cobb-Douglas a avut o contribuție de capital 1/4 la creșterea industriei prelucrătoare și 3/4 a forței de muncă, astfel încât funcția de producție C-D este

Q = AL3/4 C1/4

care arată randamente constante la scară deoarece totalul valorilor l și (3/4 + 1/4), adică, (a + 1) . Coeficientul de muncitor în funcția C-D măsoară creșterea procentuală în (Q care ar rezulta dintr-o creștere de 1% În L, în timp ce se menține ca constantă a lui Ecuador.

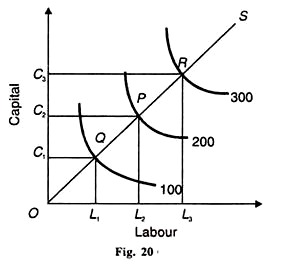
în mod similar, la nivel de procent, În Q se înregistrează o creștere de 1% în C, în timp ce L este constant. Funcția de producție C-D care prezintă randamente constante la scară este descrisă în Figura 20. Forța de muncă este luată pe axa orizontală și capitalul pe axa verticală.

pentru a produce 100 de unități de producție, se folosesc unități de capital și unități de muncă ol. Dacă producția ar fi dublată la 200, intrările de muncă și capital ar trebui dublate. De asemenea, numărul de ore pe zi este de două ori mai mare decât numărul de ore pe zi, iar numărul de ore pe zi este egal cu numărul de ore pe zi.

în mod similar, dacă producția va fi crescută de trei ori la 300, unitățile de muncă și capital vor trebui majorate de trei ori. OC3 și OL3 sunt de trei ori mai mari decât cele de la OL1 și, respectiv, OL1. O altă metodă este de a lua linia de scară sau calea de expansiune care leagă punctele de echilibru Q, P și R. OS este linia de scară sau calea de expansiune care unește aceste puncte.

arată că izoquanții 100, 200 și 300 sunt echidistanți. Astfel, pe linia de scară OS OQ = QP = PR care arată că atunci când capitalul și forța de muncă sunt crescute în proporții egale, producția crește și în aceeași proporție.

critici ale funcției de producție C-D:

funcția de producție C-D a fost criticată de Arrow, Chenery, Minhas și Solow după cum se discută mai jos:

1. Funcția de producție C-D ia în considerare doar două intrări, forța de muncă și capitalul și neglijează unele intrări importante, cum ar fi materiile prime, care sunt utilizate în producție. Prin urmare, nu este posibilă generalizarea acestei funcții la mai mult de două intrări.

2. În funcția de producție C-D, problema măsurării capitalului apare deoarece este nevoie doar de cantitatea de capital disponibilă pentru producție. Dar utilizarea deplină a capitalului disponibil poate fi făcută numai în perioade de angajare deplină. Acest lucru este nerealist, deoarece nicio economie nu este întotdeauna pe deplin angajată.

3. Funcția de producție C-D este criticată deoarece arată randamente constante la scară. Dar randamentele constante la scară nu sunt o realitate, deoarece randamentele crescătoare sau descrescătoare la scară sunt aplicabile producției.

nu este posibilă modificarea tuturor intrărilor pentru a aduce o schimbare proporțională a rezultatelor tuturor industriilor. Unele intrări sunt rare și nu pot fi crescute în aceeași proporție cu intrările abundente. Pe de altă parte, intrări precum mașini, antreprenoriat etc. sunt indivizibile. Pe măsură ce producția crește datorită utilizării factorilor indivizibili la capacitatea lor maximă, costul unitar scade.

astfel, atunci când furnizarea de intrări este limitată și indivizibilitățile sunt prezente, nu sunt posibile reveniri constante la scară. Ori de câte ori unitățile de intrări diferite sunt crescute în procesul de producție, economiile de scară și specializare duc la creșterea randamentelor la scară. cu toate acestea, în practică, Niciun antreprenor nu va dori să crească diferitele unități de intrări pentru a avea o creștere proporțională a producției. Efortul său este de a avea o creștere mai mult decât proporțională a producției, deși nu sunt excluse și randamentele în scădere la scară.

4. Funcția de producție C-D se bazează pe presupunerea substituibilității factorilor și neglijează complementaritatea factorilor.

5. Această funcție se bazează pe presupunerea unei concurențe perfecte pe piața factorilor, care este nerealistă. Cu toate acestea, dacă se renunță la această ipoteză, coeficienții sec.

6. Una dintre punctele slabe ale funcției C-D este problema agregării. Această problemă apare atunci când această funcție este aplicată fiecărei firme dintr-o industrie și întregii industrii. În această situație, vor exista multe funcții de producție de agregare scăzută sau ridicată. Astfel, funcția C-D nu măsoară ceea ce își propune să măsoare.

concluzie:

astfel, practicabilitatea funcției de producție A C-D în industria prelucrătoare este o propunere îndoielnică. Acest lucru nu se aplică agriculturii în care, pentru cultivarea intensivă, creșterea cantităților de inputuri nu va crește producția proporțional. Chiar și atunci, nu se poate nega faptul că revenirea constantă la scară este o etapă în viața unei firme, a unei industrii sau a unei economii. Este un alt lucru că această etapă poate veni după ceva timp și pentru o perioadă scurtă de timp.

este important:

În ciuda acestor critici, funcția C-D este de mare importanță.

1. A fost utilizat pe scară largă în studiile empirice ale industriilor prelucrătoare și în comparațiile interindustriale.

2. Este folosit pentru a determina ponderea relativă a forței de muncă și a capitalului în producția totală.

3. Este folosit pentru a demonstra teorema lui Euler.

4. Parametrii săi a și b reprezintă coeficienți de elasticitate care sunt utilizați pentru comparații intersectoriale.

5. Această funcție de producție este liniară omogenă de gradul unu, care arată randamente constante la scară, în cazul în care se înregistrează randamente în creștere la scară, iar în cazul în care se înregistrează randamente în creștere la scară, în cazul în care se înregistrează randamente în scădere la scară, iar în cazul în care se înregistrează randamente în scădere la scară.

6. Economiștii au extins această funcție de producție la mai mult de două variabile.