Articles

notația funcției și modul de evaluare a unei funcții

by admin

notația comună a unei funcții este de obicei scrisă ca,

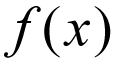
f(x) înseamnă f este o expresie care implică variabila x

nu vă gândiți la asta prea literal, adică F este înmulțit cu X. În schimb, ia în considerare acest lucru ca o expresie matematică care este citit ca

f este o funcție de x

sau

F este o expresie care conține variabila sau litera X

funcțiile pot fi, de asemenea, scrise în moduri diferite folosind alte variabile, cum ar fi

  • g(x), H(X) și K(x)

în plus, funcțiile pot lua alte valori de intrare, altele decât x.

  • f(A), h(r), și k(m)

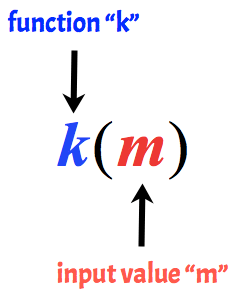
ideea cheie este întotdeauna să ne amintim că variabila din afara parantezei este „numele” funcției, în timp ce variabila din interiorul parantezei este valoarea funcției.

de exemplu, următoarele se numește funcția k cu o valoare de intrare de m.

k(m) poate fi citit ca funcția de k de m. aceasta înseamnă că funcția k este exprimată în termeni de m, deoarece m este valoarea de intrare.

Exemple de bază de evaluare a funcțiilor

Exemplul 1: evaluați funcția .

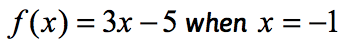
f(x) = 3x - 5 Când x=-1

aceasta este notația normală a funcției în care funcția este f în timp ce valoarea de intrare este x. pentru a evalua o funcție, ceea ce vrem este să înlocuim fiecare instanță a lui X în expresie și apoi simplificați.

deoarece x = – 1 , înlocuim această valoare în funcție și simplificăm. Procedând astfel, obținem o soluție care arată astfel.

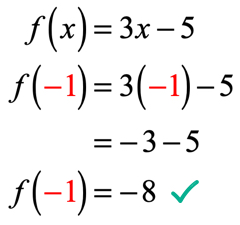
f(x) = 3x - 1(-1) = 3(-1) - 5 → f (-1) = -3 -5 = -8. prin urmare, f(-1) = -8.

Exemplul 2: evaluați funcția .

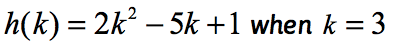
h(k) = 2k^2-5k+1 când k=3

observați că funcția de aici este h și valoarea de intrare este k. La fel ca în exemplul nostru anterior, vrem să înlocuim orice valoare numerică atribuită lui k în funcția dată și să simplificăm.

deoarece K = 3, soluția dvs. ar trebui să arate similar cu acest

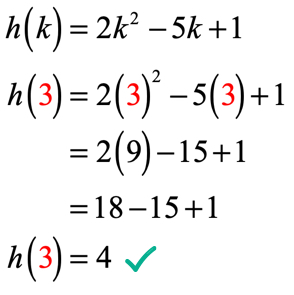
h ( k) = 2k^2 - 5K + 1(3) = 2(3)^2 - 5(3) + 1 → h(3) = 2(9) -15+1 → h(3) = 18 - 15 + 1 → h (3) = 4.

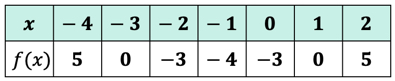
Exemplul 3: evaluați fiecare valoare a lui x din tabelul de mai jos folosind funcția de mai jos. Trasați punctele din axa xy și conectați punctele pentru a dezvălui graficul funcției.

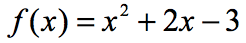
f(x) = x^2 + 2x - 3

un tabel de valori pentru funcția f de X sau f(x) unde valorile X sunt -4, -3, -2, -1, 0, 1 și 2

deoarece există șapte intrări x, asta înseamnă că vom evalua funcția de șapte ori, de asemenea. Încercați să lucrați singur, apoi reveniți pentru a vă verifica răspunsurile.

dacă ați făcut-o corect, acestea sunt valorile:

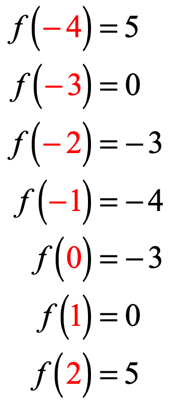
acestea sunt valorile funcției atunci când sunt evaluate cu fiecare valoare x sau valoare de intrare. f (-4) = 5, f(-3)=0, f(-2) = -3, f(-1) = -4, f(0) = -3, f(1) = 0, f(2) = 5.

acum putem plasa acele valori de ieșire în tabel.

iată tabelul complet al valorilor reprezentate ca un set de perechi ordonate: { (-4,5), (-3,0), (-2,-3), (-1,-4), (0,-3), (1,0), (2,5) }

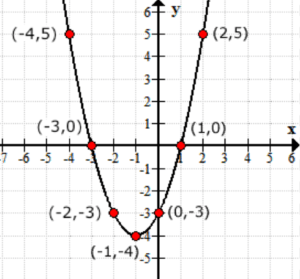
gândiți-vă la valorile de ieșire ale funcției f\stânga( x \dreapta) ca valori Y. Așa arată graficul pe axa xy.

după trasarea punctelor din tabelul generat de funcția f(x) = x^2 + 2x -3 obținem o parabolă care se deschide cu un minim la (-1,-4), y-intercept de -3 și X-interceptări de -3 și 1.

Exemple intermediare de evaluare a funcțiilor

Exemplul 4: având în vedere că G\stânga( x \dreapta) = {x^2} – 3x + 1, Găsiți g\stânga( {2x – 1} \dreapta).

în exemplele anterioare, am evaluat o funcție cu un număr. De data aceasta valoarea de intrare nu mai este o valoare numerică fixă, ci o expresie. Ar putea părea complicat, dar procedura rămâne aceeași.

vom înlocui fiecare instanță a lui x în g\stânga( x \dreapta) cu valoarea de intrare care este 2x – 1. Simplificați prin pătratul binomului, aplicând proprietatea distributivă și combinând termeni asemănători.

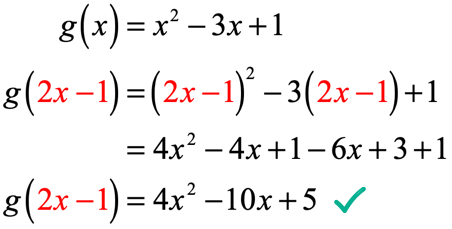
g(x)=x^2-3x+1 g(2x-1) = (2x-1)^2 - 3(2x-1) +1 g(2x-1) = 4x^2-4x+1-6x+3=1 g(2x-1) = 4x^2 - 10x + 5

exemplul 5: având în vedere că p\stânga( x \dreapta) = {{4x – 1} \peste x} , evaluați p\stânga( 1 \dreapta) – p\stânga( { – 1} \dreapta).

problema poate părea intimidantă la început, dar odată ce o analizăm și aplicăm ceea ce știm deja despre cum să evaluăm funcțiile, acest lucru nu ar trebui să fie atât de rău!

ceea ce trebuie să facem aici este să evaluăm funcția la x = 1,apoi să scădem cu valoarea funcției atunci când este evaluată la x= -\, 1.

fiți foarte atenți atunci când înlocuiți valorile și în timpul procesului de simplificare. Dacă nu sunteți atent la fiecare pas, este foarte ușor să comiteți greșeli atunci când adăugați, scădeți, înmulțiți sau împărțiți numere pozitive și negative.

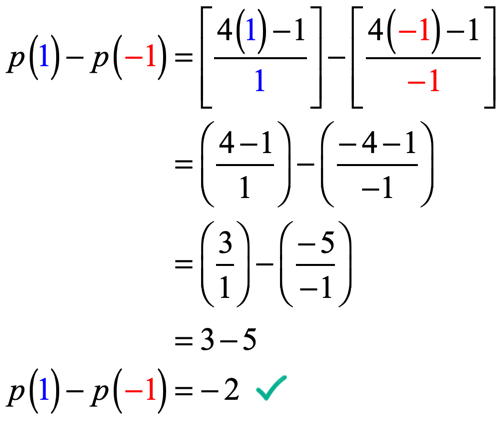
p (1) - p(-1) = { /(1) } - { /(-1) } = - = 3-5 → p (1) - p(-1) = -2

exemplu avansat de aplicare a conceptului de evaluare a funcțiilor

exemplul 6: Dacă f\stânga( 2 \dreapta) = 9, găsiți valoarea a în funcția de mai jos.

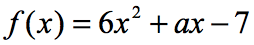
f(x) = 6X^2 + ax -7, găsiți valoarea unui

în ecuație, F\stânga( 2 \dreapta) = 9, ni se spune că, dacă intrarea funcția este 2; rezultatul funcției va fi 9. Deoarece funcția ne este dată, prima noastră mișcare este să înlocuim cel puțin valoarea lui 2 și apoi să simplificăm. Aceasta este ceea ce vom obține.

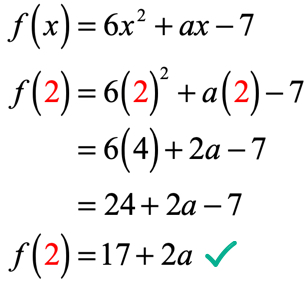
f (x) = 6X^2 + ax - 7(2) = 6(2)^2 + a(2) - 7 F(2) = 6(4) +2a - 7 = 24 + 2a-7 F( 2) = 17 + 2A

ieșirea funcției după evaluarea la x = 2 este 17 + 2a. amintiți-vă, ni se spune, de asemenea, că ieșirea este 9 folosind ecuația dată f\stânga (2 \dreapta) = 9. Prin urmare, ceea ce trebuie să facem acum este să le setăm egale între ele și să rezolvăm ecuația liniară pentru valoarea necunoscută a lui a.

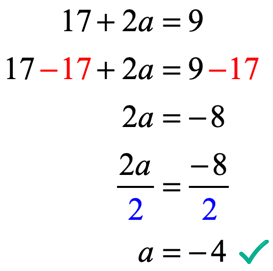
17 + 2A = 9,17-17+2a = 9-17, 2a -8 (2A)/2 = -8/2) a = -4

să verificăm dacă valoarea lui a= -\, 4 în f(x) = 6{x^2} + ax – 7 poate face condiția dată F\stânga( 2 \dreapta) = 9 să fie o afirmație adevărată.

f(x) = 6X^2 - 4x -7(2) = 6(2)^2 - 4(2) - 7 = 6(4) - 8- 7 = 24 - 8 - 7 → f (2)=9

este adevărat! Prin urmare, am rezolvat cu succes pentru valoarea corectă a lui a.