un test de normalitate alternativă este testul Shapiro-Wilk.

• ce este un test de normalitate Kolmogorov-Smirnov?
• testul SPSS Kolmogorov-Smirnov din testele NPAR
• testul SPSS Kolmogorov-Smirnov din examinarea variabilelor
• raportarea unui Test Kolmogorov-Smirnov
• rezultate greșite în SPSS?

ce este un test de normalitate Kolmogorov-Smirnov?

testul Kolmogorov-Smirnov examinează dacă scorurile
sunt susceptibile să urmeze o anumită distribuție în unele populații.Pentru a evita confuzia, există 2 teste Kolmogorov-Smirnov:

• există un test Kolmogorov-Smirnov pentru testare dacă o variabilă urmează o distribuție dată într-o populație. Această” distribuție dată „este de obicei-nu întotdeauna – distribuția normală, prin urmare”testul de normalitate Kolmogorov-Smirnov”.
• există, de asemenea, probele independente (mult mai puțin frecvente) testul Kolmogorov-Smirnov pentru testarea dacă o variabilă are distribuții identice în 2 populații.

în teorie, „testul Kolmogorov-Smirnov” s-ar putea referi la oricare dintre teste (dar de obicei se referă la testul Kolmogorov-Smirnov cu un singur eșantion) și ar fi bine să fie evitat. Apropo, ambele teste Kolmogorov-Smirnov sunt prezente în SPSS.

testul Kolmogorov-Smirnov – exemplu simplu

deci, spuneți că am o populație de 1.000.000 de oameni. Cred că timpii lor de reacție pe unele sarcini sunt perfect distribuite în mod normal. Am eșantionat 233 dintre acești oameni și le-am măsurat timpul de reacție.acum, distribuția de frecvență observată a acestora va diferi probabil un pic – dar nu prea mult-de o distribuție normală. Așa că rulez o histogramă peste timpii de reacție observați și suprapun o distribuție normală cu aceeași medie și deviație standard. Rezultatul este prezentat mai jos.

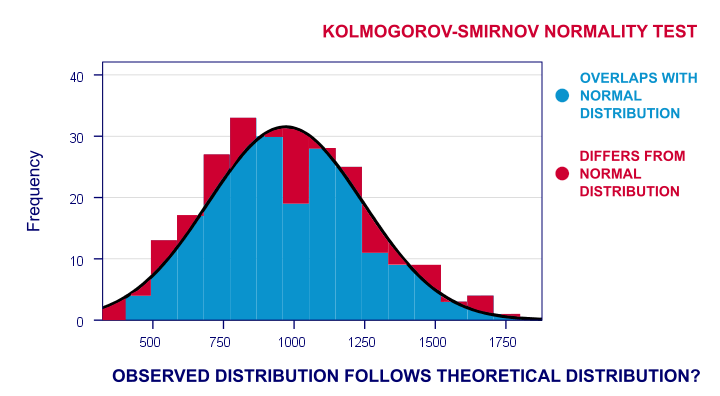
distribuția frecvenței scorurilor mele nu se suprapune în întregime cu curba mea normală. Acum, aș putea calcula procentul de cazuri care se abat de la curba normală-procentul de zone roșii din diagramă. Acest procent este o statistică de testare: exprimă într-un singur număr cât de mult diferă datele mele de ipoteza mea nulă. Deci, indică în ce măsură scorurile observate se abat de la o distribuție normală.
acum, dacă ipoteza mea nulă este adevărată, atunci acest procent de abatere ar trebui să fie probabil destul de mic. Adică, o mică abatere are o valoare de probabilitate mare sau o valoare P.
invers, un procent uriaș de deviație este foarte puțin probabil și sugerează că timpii mei de reacție nu urmează o distribuție normală în întreaga populație. Deci, o abatere mare are o valoare p scăzută. Ca regulă generală, wereject ipoteza nulă dacă p < 0.05.So dacă p < 0.05, nu credem că variabila noastră urmează o distribuție normală în populația noastră.

testul Kolmogorov-Smirnov – Statistica testului

deci, acesta este cel mai simplu mod de a înțelege cum funcționează testul de normalitate Kolmogorov-Smirnov. Cu toate acestea, din punct de vedere computațional, funcționează diferit: compară frecvențele relative cumulative observate față de cele așteptate, așa cum se arată mai jos.

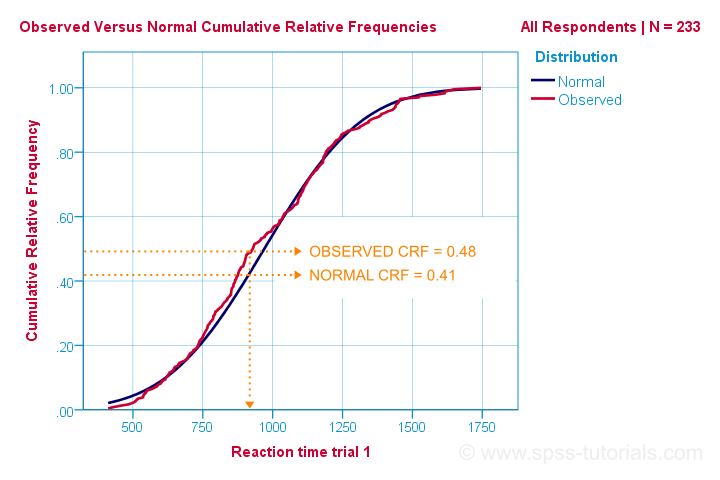
testul Kolmogorov-Smirnov folosește diferența absolută maximă dintre aceste curbe ca Statistică de testare notată cu D. În această diagramă, diferența absolută maximă D este (0,48 – 0,41 =) 0,07 și apare la un timp de reacție de 960 milisecunde. Rețineți că D = 0.07 așa cum îl vom întâlni în ieșirea noastră SPSS într-un minut.

testul Kolmogorov-Smirnov în SPSS

există 2 moduri de a rula testul în SPSS:

• teste NPAR așa cum se găsește în analiza teste neparametrice Legacy Dialogs 1-eșantion K-S… este metoda noastră de alegere, deoarece creează o ieșire frumos detaliată.
• examinați variabilele din analiza Descriptive Statistics Explore este o alternativă. Această comandă rulează atât testul Kolmogorov-Smirnov, cât și testul de normalitate Shapiro-Wilk.
  rețineți că examinarea variabilelor utilizează excluderea listwise a valorilor lipsă în mod implicit. Deci, dacă testez 5 variabile, cele 5 teste ale mele folosesc doar cazuri care nu au nicio lipsă pe niciuna dintre aceste 5 variabile. Acest lucru nu este, de obicei, ceea ce vrei, dar vom arăta cum să evite acest lucru.

vom demonstra ambele metode folosind speedtasks.sav pe tot parcursul, o parte din care este prezentată mai jos.

întrebarea noastră principală de cercetare estecare dintre variabilele timpului de reacție este probabil
să fie distribuite în mod normal în populația noastră?Aceste date sunt un exemplu de manual de ce ar trebui să inspectați cu atenție datele înainte de a începe să le editați sau să le analizați. Să facem doar asta și să rulăm câteva histograme din sintaxa de mai jos.

rezultat

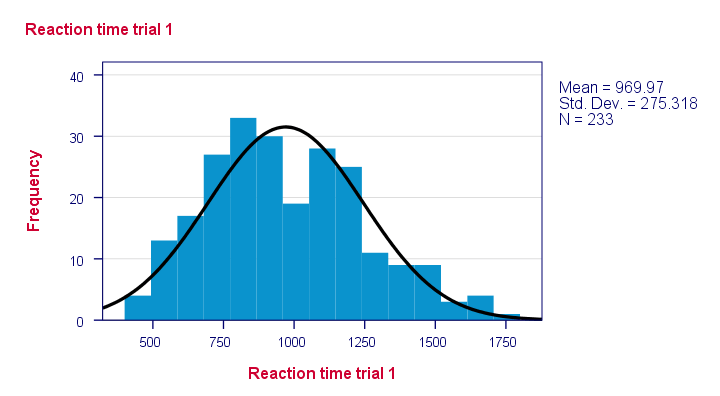
rețineți că unele distribuții nu par deloc plauzibile. Dar care sunt susceptibile de a fi distribuite în mod normal?

testul SPSS Kolmogorov-Smirnov din testele NPAR

opțiunea noastră preferată pentru rularea testului Kolmogorov-Smirnov este subanalyze teste neparametrice Dialoguri moștenite 1-eșantion K-S… după cum se arată mai jos.

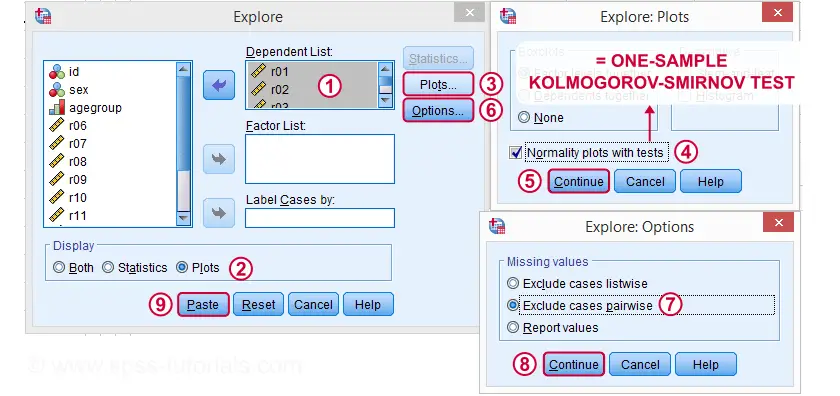
apoi, vom completa doar dialogul așa cum se arată mai jos.

clic Paste rezultate în sintaxa de mai jos. Să-l rulați.

sintaxa testului Kolmogorov-Smirnov din testele neparametrice

rezultate

în primul rând, rețineți că statistica testului pentru prima noastră variabilă este 0.073-la fel cum am văzut în graficul nostru de frecvențe relative cumulative un pic mai devreme. Graficul conține exact aceleași date pe care tocmai le-am efectuat testul, astfel încât aceste rezultate converg frumos.în ceea ce privește întrebarea noastră de cercetare: numai timpii de reacție pentru trial 4 par a fi distribuite în mod normal.

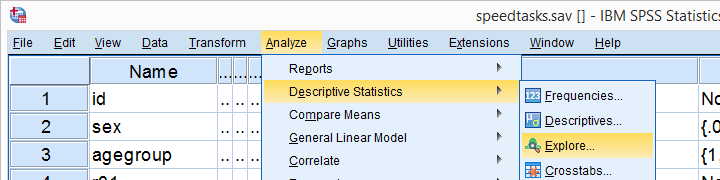
testul SPSS Kolmogorov-Smirnov din examinarea variabilelor

o modalitate alternativă de a rula testul Kolmogorov-Smirnov pornește de la analiza statistici Descriptive Exploreas prezentată mai jos.

Kolmogorov-Smirnov test Sintaxa de teste neparametrice

Results

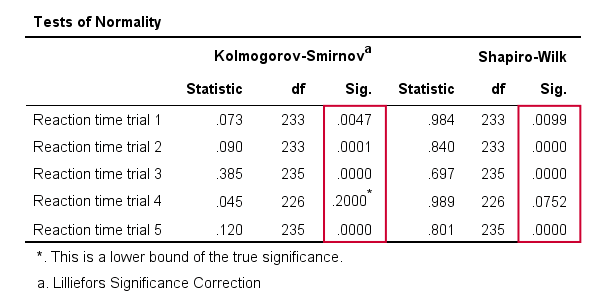
As a rule of thumb, we conclude thata variable is not normally distributed if „Sig.” < 0.05.Deci, atât testul Kolmogorov-Smirnov, cât și rezultatele testului Shapiro-Wilk sugerează că doar studiul timpului de reacție 4 urmează o distribuție normală în întreaga populație.mai mult, rețineți că rezultatele testului Kolmogorov-Smirnov sunt identice cu cele obținute din testele NPAR.

raportarea unui test Kolmogorov-Smirnov

pentru raportarea rezultatelor testelor noastre urmând instrucțiunile APA, vom scrie ceva de genul”un test Kolmogorov-Smirnov indică faptul că timpii de reacție din Studiul 1 nu urmează o distribuție normală, D(233) = 0,07, p = 0,005.”Pentru variabile suplimentare, încercați să scurtați acest lucru, dar asigurați-vă că includeți

• D (pentru „diferență”), statistica testului Kolmogorov-Smirnov,
• df, gradele de libertate (care este egal cu N) și
• p, semnificația statistică.

rezultate greșite în SPSS?

dacă sunteți un student care vrea doar să treacă un test, puteți opri citirea acum. Doar urmați pașii pe care i-am discutat până acum și veți fi bine.

dreapta, acum să ruleze exact aceleași teste din nou în SPSS versiunea 18 și să ia o privire la ieșire.

în această ieșire, valorile P exacte sunt incluse și-din fericire-sunt foarte apropiate de valorile P asimptotice. Mai puțin din fericire, totuși, rezultatele SPSS version 18 Sunt extrem de diferite
De rezultatele SPSS version 24 pe care le-am raportat până acum.
motivul pare a fi corectarea semnificației Lilliefors care se aplică în versiunile SPSS mai noi. Rezultatul pare să fie că nivelurile de semnificație asimptotică diferă mult mai mult de semnificația exactă decât au făcut-o atunci când corecția nu este implicită. Acest lucru ridică îndoieli serioase cu privire la corectitudinea „rezultatelor Lilliefors” -implicit în versiunile SPSS mai noi.
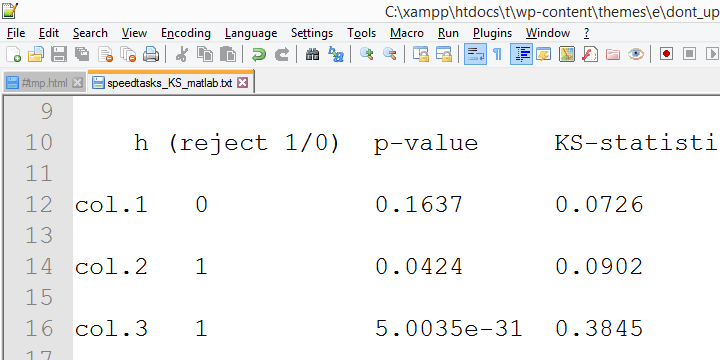
dovezi convergente pentru această sugestie au fost adunate de colegul meu Alwin Stegeman care a reluat toate testele în Matlab. Rezultatele Matlab sunt de acord cu rezultatele SPSS 18 și – prin urmare-nu cu rezultatele mai noi.

test de normalitate Kolmogorov – Smirnov-utilitate limitată

testul Kolmogorov – Smirnov este adesea pentru a testa presupunerea de normalitate cerută de multe teste statistice, cum ar fi ANOVA, testul t și multe altele. Cu toate acestea, este aproape în mod obișnuit trecut cu vederea faptul că astfel de teste sunt robuste împotriva unei încălcări a acestei presupuneri dacă dimensiunile eșantionului sunt rezonabile, să zicem n 25.Motivul principal pentru aceasta este teorema limitei centrale. Prin urmare, testele de normalitate sunt necesare numai pentru dimensiunile mici ale eșantionuluidacă scopul este de a satisface ipoteza normalității.
din păcate, dimensiunile mici ale eșantioanelor au ca rezultat o putere statistică scăzută pentru testele de normalitate. Aceasta înseamnă că abaterile substanțiale de la normalitate nu vor avea ca rezultat o semnificație statistică. Testul spune că nu există nici o abatere de la normalitate în timp ce este de fapt imens. Pe scurt, Situația în care sunt necesare teste de normalitate-dimensiuni mici ale eșantioanelor – este, de asemenea, situația în care acestea au performanțe slabe.

Vă mulțumim pentru lectură.