příjmy jsou množství peněz, které společnost přináší. V tomto případě lze příjmy zjistit vynásobením ceny za předplatné násobkem počtu účastníků nebo množství. Můžeme zavést proměnné, p pro cenu za předplatné a Q pro množství, což nám dává rovnici \text{Revenue}=pQ.

protože se počet účastníků mění s cenou, musíme najít vztah mezi proměnnými. Víme, že v současné době p=30 A Q=84,000. Také víme, že jestliže cena vzroste na $32, noviny by ztratit 5,000 uživatelů, přičemž druhý pár hodnot, p=32 a Q=79 000 v. Z toho můžeme najít lineární rovnici týkající se dvou veličin. Na svahu bude

\begin{align}m&=\dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{-5,000}{2} \\ &=-2,500 \end{align}

To nám říká, že papír ztratí 2,500 odběratelé za každý dolar se zvýší cena. Pak můžeme vyřešit pro y-intercept.

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.

\begin{align}&\text{Příjem}=pQ \\ &\text{Příjem}=p\left(-2,500 p+159,000\right) \\ &\text{Příjem}=-2,500{p}^{2}+159,000 p \end{align}

nyní Máme kvadratickou funkci pro příjmy jako funkce předplatného zdarma. Chcete-li najít cenu, která maximalizuje příjmy pro noviny, najdeme vrchol.

\begin{align}h&=-\dfrac{159,000}{2\left(-2,500\right)} \\ &=31.8 \end{align}

model nám říká, že maximální příjmy bude dojít, pokud noviny poplatky $31.80 pro předplatné. Abychom zjistili, jaký je maximální příjem, vyhodnocujeme funkci příjmů.

\begin{align}\text{maximální příjmy}&=-2,500{\left(31.8\right)}^{2}+159,000\left(31.8\right) \\ &=\$2,528,100\hfill \end{align}

Analýza Řešení

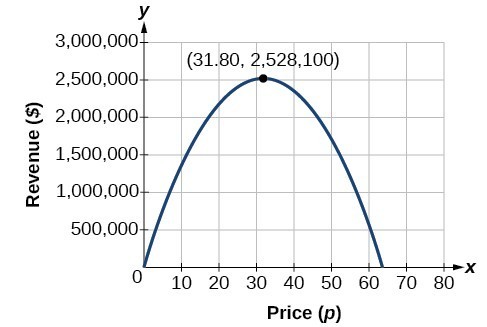
To může být také vyřešen pomocí grafů kvadratické. Maximální výnos můžeme vidět na grafu kvadratické funkce.