Le revenu est le montant d’argent qu’une entreprise apporte. Dans ce cas, le revenu peut être trouvé en multipliant le prix par abonnement par le nombre d’abonnés, ou la quantité. Nous pouvons introduire des variables, p pour le prix par abonnement et Q pour la quantité, nous donnant l’équation \text{Revenue} = pQ.

Comme le nombre d’abonnés change avec le prix, nous devons trouver une relation entre les variables. Nous savons qu’actuellement p = 30 et Q = 84 000. Nous savons également que si le prix monte à 32 $, le journal perdrait 5 000 abonnés, ce qui donnerait une deuxième paire de valeurs, p = 32 et Q = 79 000. De là, nous pouvons trouver une équation linéaire reliant les deux grandeurs. La pente sera

\begin{align}m&=\dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{-5,000}{2}\\&=-2,500\end{align}

Cela nous indique que le journal perdra 2,500 abonnés pour chaque dollar qu’il augmente le prix. Nous pouvons alors résoudre pour l’interception y.

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.

\begin {align}&\text{Revenue}= pQ\\&\text{Revenue}= p\left(-2 500 p + 159 000 \right) \\&\text{Revenue} = -2 500{p}^{2} + 159 000p\end{align}

Nous avons maintenant une fonction quadratique pour les revenus en fonction des frais d’abonnement. Pour trouver le prix qui maximisera les revenus du journal, nous pouvons trouver le sommet.

\begin {align}h&=-\dfrac{159,000}{2\left (-2,500\right)}\\&=31.8\end{align}

Le modèle nous indique que le revenu maximal se produira si le journal facture 31,80 $ pour un abonnement. Pour trouver le revenu maximal, nous évaluons la fonction de revenu.

\begin{align}\text{revenu maximal}&= -2 500 {\left(31,8\right)}^{2} +159 000\left(31,8\right)\\& = \$2,528,100\hfill\end {align}

Analyse de la Solution

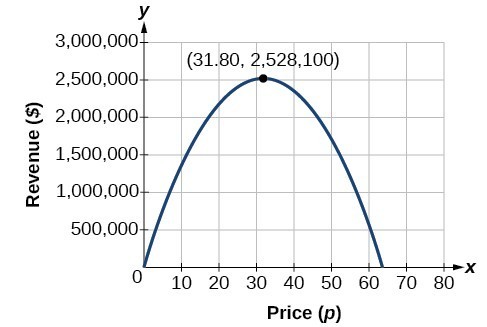
Ceci peut également être résolu en graphisant le quadratique. Nous pouvons voir le revenu maximum sur un graphique de la fonction quadratique.