Der Umsatz ist der Geldbetrag, den ein Unternehmen einbringt. In diesem Fall kann der Umsatz ermittelt werden, indem der Preis pro Abonnement mit der Anzahl der Abonnenten oder der Menge multipliziert wird. Wir können Variablen einführen, p für Preis pro Abonnement und Q für Menge, Geben Sie uns die Gleichung \ text {Umsatz} = pQ.

Da sich die Anzahl der Abonnenten mit dem Preis ändert, müssen wir eine Beziehung zwischen den Variablen finden. Wir wissen, dass derzeit p = 30 und Q = 84.000. Wir wissen auch, dass die Zeitung bei einem Preisanstieg auf 32 US-Dollar 5.000 Abonnenten verlieren würde, was ein zweites Wertepaar ergibt, p = 32 und Q = 79.000. Daraus können wir eine lineare Gleichung finden, die die beiden Größen in Beziehung setzt. Die Steigung wird sein

\begin{align}m&=\dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{-5,000}{2} \\ &= -2,500 \end{align}

Dies sagt uns, dass das Papier 2,500 Abonnenten für jeden Dollar verlieren wird, den sie den Preis erhöhen. Wir können dann nach dem y-Schnittpunkt lösen.

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.

\begin{align}&\text{Umsatz}=pQ \\ &\text{Umsatz}=p\links(-2.500 p+159.000 \rechts) \\ &\text{Revenue}= -2.500{p}^{2}+159.000p \end{align}

Wir haben jetzt eine quadratische Funktion für den Umsatz als Funktion der Abonnementgebühr. Um den Preis zu finden, der den Umsatz für die Zeitung maximiert, können wir den Scheitelpunkt finden.

\begin{align}h&=-\dfrac{159.000}{2\links(-2.500\rechts)} \\ &=31.8 \end{align}

Das Modell sagt uns, dass der maximale Umsatz erzielt wird, wenn die Zeitung 31,80 USD für ein Abonnement berechnet. Um herauszufinden, wie hoch der maximale Umsatz ist, bewerten wir die Umsatzfunktion.

\begin{align}\text{maximaler Umsatz}&=-2.500{\left(31.8\right)}^{2}+159.000\left(31.8\right) \\ &=\$ 2,528,100\hfill \end{align}

Analyse der Lösung

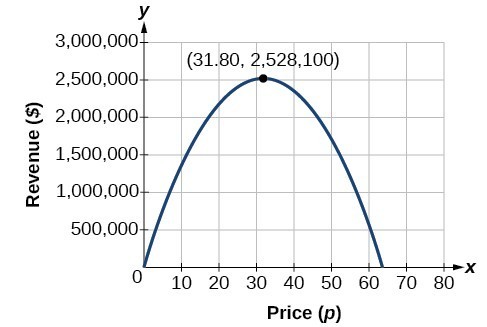
Dies könnte auch durch graphische Darstellung der quadratischen gelöst werden. Wir können den maximalen Umsatz in einem Diagramm der quadratischen Funktion sehen.