Hablando en términos de confiabilidad, paralelo, significa que cualquiera de los elementos en estructura paralela permiten que el sistema funcione. Esto no significa que sean físicamente paralelos (en todos los casos), ya que los condensadores en paralelo proporcionan un comportamiento específico en el circuito y si un condensador falla, el sistema podría fallar.
En este simple dibujo, hay n componentes en paralelo y se necesita cualquier componente para que el sistema funcione.

Si el componente #2 falla, los otros permitirán que el sistema funcione.

Simple. Y, muy útil. Esta construcción permite mejorar la fiabilidad en general, incluso por encima de la fiabilidad de los componentes individuales. A diferencia del sistema en serie, donde el componente más débil limita la confiabilidad, aquí, al agregar redundancia, la confiabilidad del sistema mejora.

Considere un sistema paralelo de dos componentes. Si ambos componentes funcionan, entonces el sistema funciona. Si falla cualquiera de los componentes 1 o 2, el sistema sigue funcionando. Si y solo si ambos componentes fallan, el sistema fallará. A diferencia de un sistema en serie en el que cualquier fallo causa un fallo del sistema, en este ejemplo simple, dos eventos de fallo tienen que ocurrir antes de que el sistema falle.

¿Cuál es la probabilidad de tener dos fallos? La fórmula se basa en la probabilidad de que el componente 1 o el componente 2 funcionen. Sin hacer la derivación, podemos escribir la confiabilidad del sistema paralelo de 2 componentes como:

Esto se complica rápidamente con más de tres componentes en paralelo. Antes de explorar otra forma de calcular sistemas paralelos, hay que mencionar primero una situación de caso especial.

Cuando los componentes en paralelo es el mismo (fiabilidad sabio), entonces lo anterior se simplifica a

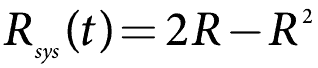
Que debería ser obvio.

A menudo es más fácil hacer cálculos de sistemas paralelos utilizando la falta de fiabilidad, o 1 – R(t). Este es también el CDF o F (t). La matemática es ahora más como un sistema de series con una corrección. Para el caso general, la fórmula de confiabilidad del sistema para un sistema paralelo se convierte en

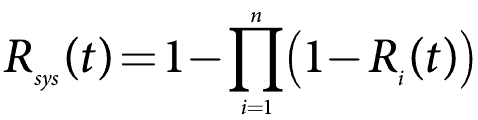
Así que, digamos que tenemos cinco componentes con Confiabilidad a un año de uso, R(1), al 90%, o 0.9. Calcule la fiabilidad del sistema.

Utilizando la fórmula anterior y establecer la confiabilidad de cada elemento en el 0,9, nos encontramos

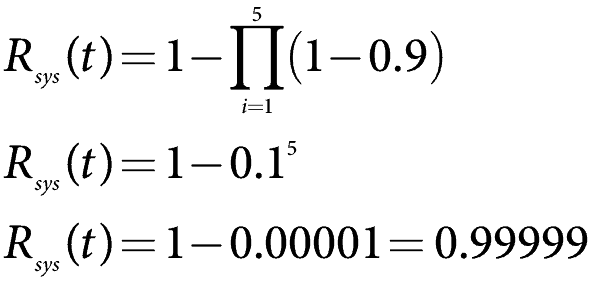
que es muy fiable.

Es costoso agregar piezas redundantes a un sistema, sin embargo, en algunos casos, es la solución correcta para crear un sistema que cumpla con los requisitos de confiabilidad. Por supuesto, los sistemas reales tienen muchas variaciones y complicaciones sobre la simple configuración de componentes en paralelo. Los sistemas de distribución de carga, de espera caliente, caliente o fría, de conmutación o de votación y muchos otros pueden complicar la construcción de un sistema paralelo.

El uso de componentes en paralelo es la única forma de aumentar la fiabilidad del sistema por encima de los límites de la fiabilidad de los componentes individuales.

Relacionada:

Diagramas de Bloques de Confiabilidad Descripción y Valor (artículo)

la Fiabilidad de Reparto (artículo)

k de n (artículo)