alla mainittu artikkeli antaa lähikuvan Cobb-Douglas-Tuotantofunktiosta.

Cobb-Douglas-tuotantofunktio perustuu Paul H. Douglasin ja C. W. Cobbin tekemään empiiriseen tutkimukseen Yhdysvaltain tehdasteollisuudesta. Se on lineaarinen homogeeninen tuotantofunktio aste yksi, joka ottaa huomioon kaksi panosta, työn ja pääoman, koko tuotoksen .teollisuus.

Cobb-Douglasin tuotantofunktio ilmaistaan seuraavasti:

Q = ALa Cß

missä Q on tuotos ja L ja С ovat vastaavasti työn ja pääoman panoksia. A, a ja β ovat positiivisia parametreja, joissa = a > o, β > O.

yhtälö kertoo, että tuotos riippuu suoraan L: stä ja C: stä, ja se osa tuotoksesta, jota ei voida selittää L: llä ja С: llä, selitetään A: lla, joka on ”jäännös”, jota usein kutsutaan tekniseksi muutokseksi.

Cobb-Douglasin ratkaisemalla tuotantofunktiolla oli 1/4 pääoman osuutta tehdasteollisuuden kasvuun ja 3/4 työvoimaa niin, että C-D tuotantofunktio on

Q = AL3/4 C1/4

, joka osoittaa vakiotuottoa asteikolle, koska L: n ja С: n arvojen yhteisarvo on yksi: (3/4 + 1/4) eli(A + β = 1) . Työvoimakerroin C-D-funktiossa mittaa prosentuaalista kasvua (Q, joka johtuisi 1 prosentin lisäyksestä L: ssä, samalla kun tilalla С on vakio.

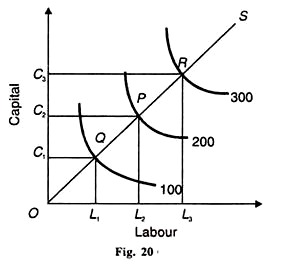
vastaavasti В on se Q: n prosentuaalinen kasvu, joka johtuisi C: n 1 prosentin kasvusta, kun taas L: ää pidetään vakiona. C-D-tuotantofunktio, joka osoittaa vakiotuottoja asteikkoon, on kuvattu kuvassa 20. Työpanos otetaan vaaka-akselille ja pääoma pystyakselille.

100 tuotosyksikön tuottamiseen käytetään ОС, pääomayksiköt ja OL työvoimayksiköt. Jos tuotanto kaksinkertaistettaisiin 200: aan, työn ja pääoman panokset olisi kaksinkertaistettava. ОС on tasan kaksi kertaa ОС1 ja OL2 on kaksinkertainen OL2.

vastaavasti, jos tuotos halutaan nostaa kolminkertaiseksi 300: aan, työ-ja pääomayksiköt on nostettava kolminkertaisiksi. OC3 ja OL3 ovat kolme kertaa suurempia kuin ОС1 ja OL1 vastaavasti. Toinen tapa on ottaa tasapainopisteet Q, P ja R yhdistävä asteikkoviiva tai laajenemispolku.OS on näitä pisteitä yhdistävä asteikkoviiva tai laajenemispolku.

sen mukaan isoquantit 100, 200 ja 300 ovat yhtä kaukana toisistaan. Näin ollen OS-asteikon linjalla oq = QP = PR, joka osoittaa, että kun pääomaa ja työvoimaa lisätään samassa suhteessa, myös tuotanto kasvaa samassa suhteessa.

kritiikki C-D-Tuotantofunktiota kohtaan:

Arrow, Chenery, Minhas ja Solow ovat kritisoineet c-d-tuotantofunktiota seuraavasti:

1. C-D-tuotantofunktio ottaa huomioon vain kaksi panosta, työn ja pääoman, ja laiminlyö joitakin tärkeitä panoksia, kuten raaka-aineita, joita käytetään tuotannossa. Tämän vuoksi funktiota ei ole mahdollista yleistää useampaan kuin kahteen tuloon.

2. C-D-tuotantofunktiossa pääoman mittaamisen ongelma syntyy siitä, että se vie vain tuotantoon käytettävissä olevan pääoman määrän. Käytettävissä olevaa pääomaa voidaan kuitenkin käyttää täysimääräisesti vain täystyöllisyyden aikana. Tämä on epärealistista, koska mikään talous ei ole aina täystyöllistetty.

3. C-D-tuotantofunktiota kritisoidaan, koska se osoittaa jatkuvaa palautumista mittakaavaan. Jatkuva palautuminen mittakaavaan ei kuitenkaan ole aktuaalisuutta, sillä tuotantoon voidaan soveltaa joko kasvavaa tai pienenevää tuottoa mittakaavaan.

kaikkia panoksia ei ole mahdollista muuttaa suhteellisesti kaikkien toimialojen tuotosten muuttamiseksi. Osa panoksista on niukkoja, eikä niitä voida lisätä samassa suhteessa kuin runsaita panoksia. Toisaalta tuotantopanokset, kuten koneet, yrittäjyys jne. ovat jakamattomia. Kun tuotanto kasvaa jakamattomien tekijöiden käytön vuoksi niiden maksimikapasiteettiin, yksikkökustannukset laskevat.

näin ollen kun tuotantopanosten tarjonta on vähäistä ja jakamattomuutta esiintyy, jatkuva palaaminen mittakaavaan ei ole mahdollista. Aina kun tuotantoprosessissa lisätään eri panosten yksiköitä, mittakaavaedut ja erikoistuminen johtavat kasvaviin mittakaavaetuihin.

käytännössä yksikään yrittäjä ei kuitenkaan halua lisätä panosten eri yksiköitä, jotta tuotanto kasvaisi suhteellisesti. Hänen pyrkimyksenään on saada aikaan enemmän kuin suhteellista tuotannon kasvua, joskaan ei ole myöskään poissuljettua, että tuotot pienenevät mittakaavaan nähden.

4. C-D-tuotantofunktio perustuu oletukseen tekijöiden korvattavuudesta ja laiminlyö tekijöiden täydentävyyden.

5. Tämä funktio perustuu olettamukseen täydellisestä kilpailusta tuotannontekijämarkkinoilla, mikä on epärealistista. Jos tästä oletuksesta kuitenkin luovutaan, kertoimet α Ja β eivät edusta tekijäosuuksia.

6. Yksi C-D-funktion heikkouksista on aggregaatio-ongelma. Tämä ongelma syntyy, kun tätä toimintoa sovelletaan jokaiseen alan yritykseen ja koko teollisuuteen. Tässä tilanteessa on monia matalan tai korkean aggregaation tuotantotoimintoja. Näin C-D-funktio ei mittaa sitä, mitä sillä pyritään mittaamaan.

johtopäätös:

näin ollen C-D-tuotantofunktion käyttökelpoisuus valmistavassa teollisuudessa on kyseenalainen väite. Tätä ei sovelleta maatalouteen, jossa tuotantopanosten määrän lisääminen tehoviljelyssä ei lisää tuotantoa samassa suhteessa. Silloinkaan ei voida kieltää, etteikö jatkuva palaaminen mittakaavaan olisi vaihe yrityksen, teollisuuden tai talouden elämässä. Se on toinen asia, että tämä vaihe voi tulla jonkin ajan kuluttua ja vähän aikaa.

sen merkitys:

kritiikistä huolimatta C-D-funktiolla on suuri merkitys.

1. Sitä on käytetty laajasti tehdasteollisuuden empiirisissä tutkimuksissa ja toimialojen välisissä vertailuissa.

2. Sitä käytetään määrittämään työn ja pääoman suhteelliset osuudet kokonaistuotannosta.

3. Sitä käytetään Eulerin lauseen todistamiseen.

4. Sen parametrit a ja b edustavat kimmokertoimia, joita käytetään sektorien välisissä vertailuissa.

5. Tämä tuotantofunktio on ensimmäisen asteen lineaarinen homogeeninen, joka osoittaa asteikon jatkuvan palautuksen, jos α + β = 1, asteikon palautukset lisääntyvät ja jos α + β < 1, asteikon palautukset vähenevät.

6. Taloustieteilijät ovat laajentaneet tämän tuotantofunktion yli kahteen muuttujaan.