funktion yleinen notaatio kirjoitetaan yleensä seuraavasti:

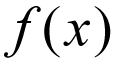
älä ajattele tätä liian kirjaimellisesti, eli F kerrotaan X: ksi. Sen sijaan pidetään tätä matemaattisena lausekkeena, joka luetaan seuraavasti:

tai

funktiot voidaan kirjoittaa myös eri tavoin käyttäen muita muuttujia, kuten

• g(x), H(x) ja K(x)

lisäksi funktiot voivat ottaa muut tuloarvot kuin x.

• f(A), h(r) ja k(m)

keskeinen ajatus on aina muistaa, että suluissa oleva muuttuja on funktion ”nimi”, kun taas suluissa oleva muuttuja on tuloarvo funktio.

esimerkiksi seuraavaa kutsutaan funktioksi k, jonka tuloarvo on m.

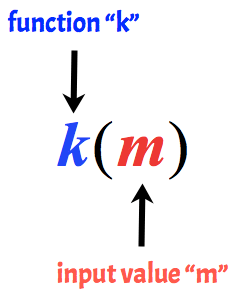
perusesimerkkejä funktioiden arvioinnista

Esimerkki 1: Arvioi funktio .

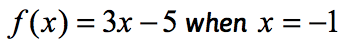
Tämä on funktion normaali notaatio, jossa funktio on f kun taas tuloarvo on x. korvaa jokainen ilmentymä x lausekkeessa ja sitten yksinkertaistaa.

koska x = – 1 , korvaamme tämän arvon funktiossa ja yksinkertaistamme. Näin saamme tämän näköisen ratkaisun.

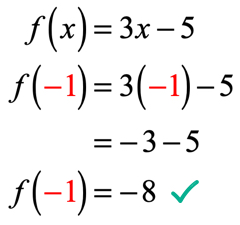
Esimerkki 2: Evaluate the function .

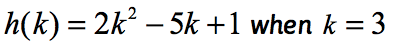
huomaa, että funktio tässä on H ja tuloarvo k. Aivan kuten edellisessä esimerkissä, haluamme korvata mitä tahansa numeerinen arvo määritetty k osaksi tietyn funktion, ja yksinkertaistaa.

koska K = 3, ratkaisun pitäisi näyttää samanlaiselta kuin tämä

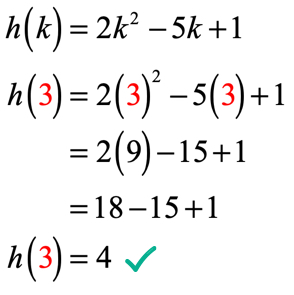
esimerkki 3: arvioi jokainen X: n arvo Alla olevassa taulukossa käyttäen alla olevaa funktiota. Piirrä pisteet xy-akselilla ja yhdistä pisteet paljastaaksesi funktion kuvaajan.

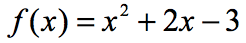
koska x-syötteitä on seitsemän, se tarkoittaa, että arvioimme funktion myös seitsemän kertaa. Yritä selvittää tämä itse ja tule sitten tarkistamaan vastauksesi.

Jos olet tehnyt sen oikein, nämä ovat arvot:

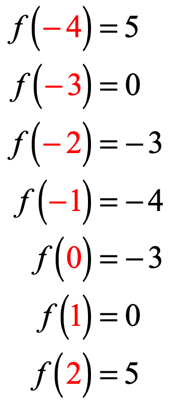
voimme nyt sijoittaa nämä lähtöarvot taulukkoon.

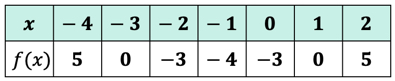
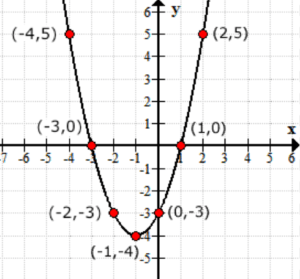
ajattele funktion F\left( x \right) lähtöarvoja y-arvoina. Tältä käyrä näyttää xy-akselilla.

Väliesimerkkejä funktioiden arvioinnista

esimerkki 4: Koska g\left( x \right) = {x^2} – 3x + 1, Etsi g\left( {2x – 1} \right).

aiemmissa esimerkeissä funktiota on arvioitu luvulla. Tällä kertaa tuloarvo ei ole enää kiinteä numeerinen arvo, vaan lauseke. Se voi näyttää monimutkaiselta, mutta menettely pysyy samana.

jokainen X: n ilmentymä g\left( x \right) korvataan tuloarvolla, joka on 2x – 1. Yksinkertaistetaan neliöimällä binomi, soveltamalla jakoomaisuutta ja yhdistämällä samanlaisia termejä.

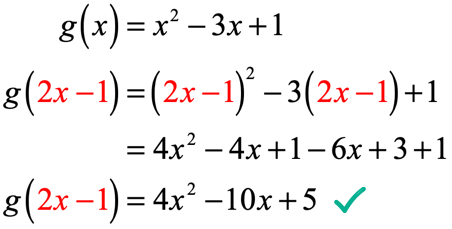
esimerkki 5: koska p\left( x \right) = {{4x – 1} \over X} , arvioi p\left( 1 \right) – p\left( { – 1} \right).

ongelma voi aluksi näyttää uhkaavalta, mutta kun analysoimme sen ja sovellamme sitä, mitä jo tiedämme funktioiden arvioinnista, tämän ei pitäisi olla niin paha!

tässä on arvioitava funktiota pisteessä x = 1 ja vähennettävä sitten funktion arvolla,kun sitä arvioidaan pisteessä x= -\, 1.

ole hyvin varovainen, kun korvaat arvot ja yksinkertaistamisprosessin aikana. Jos et ole varovainen jokaisessa vaiheessa, on erittäin helppoa tehdä virheitä, kun lisäät, vähennät, kerrot tai jaotat positiivisia ja negatiivisia lukuja.

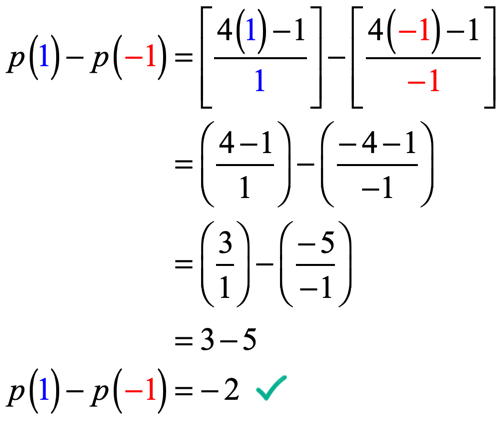
Advanced Example of Applying the Concept of Evaluating Functions

Example 6: If F\left (2 \right) = 9, find the value of a in the function below.

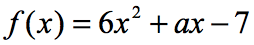
yhtälöstä F\left( 2 \right) = 9, meille kerrotaan, että jos tulo funktio on 2; funktion ulostulo on 9. Koska funktio on annettu meille, meidän ensimmäinen siirto on ainakin korvata arvo 2 ja sitten yksinkertaistaa. Tämän me saamme.

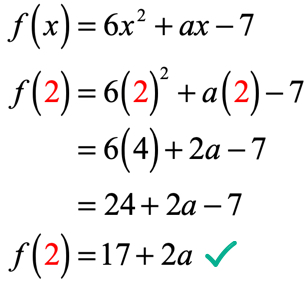
funktion tuloste x = 2 arvioinnin jälkeen on 17 + 2a. muista, että meille kerrotaan myös, että tuloste on 9 käyttäen annettua yhtälöä f\left( 2 \right) = 9. Siksi ne on nyt asetettava samansuuruisiksi keskenään ja ratkaistava lineaarinen yhtälö tuntemattomalle arvolle a.

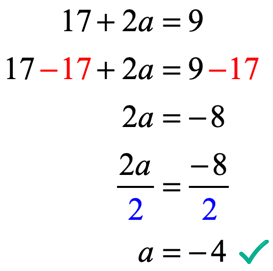
tarkistetaan, voiko annettu ehto F \left(2\right) = 9 olla tosi lausuma.

se on totta! Näin ollen olemme onnistuneesti ratkaisseet A: n oikean arvon.