tensori on joukko tietoja (numerot, funktiot jne.), joka on laajennettu tahansa määrä (0 ja suurempi) ulottuvuuksia. Ulottuvuuksien määrää kutsutaan tensorin arvoksi.

sijoitus 0 tensori

tensori, jolla ei ole mittoja (0).

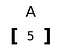
sijoitus 1 tensori

tensori, joka on laajentunut vain yhteen ulottuvuuteen.

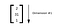
Rank 2 tensor

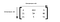
Rank 3 tensor

As shown in figure, a rank 3 tensor has a cube (or cuboid like structure).

If rank of a tensor exceeds 3, it becomes difficult to visualize.

Skalaari

skalaari on 0 rankka tensori. Fysiikassa skalaarina esitetään erilaisia suureita, kuten etäisyys (500 km), lämpötila (10ºC), nopeus (34 km/h) jne.

vektori

sijoitus 1-tensoria kutsutaan vektoriksi. Fysikaaliset suureet, kuten nopeus (10 m/s), Siirtymä (54 m itään päin), sähkömagneettinen kenttä (1 V/m).

skalaarin ja vektorin ero :

suure, joka ei vaadi sen kanssa lisätietoja (kuten suuntaa) (kuten lämpötilaa), esitetään skalaarina. Kun taas suure, joka tarvitsee suunnan määritettäväksi suuruutensa rinnalla, esitetään vektorilla (kuten sähkökentällä).

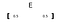
vektoria merkitään lihavoidulla kirjaimella (kuten ”e” ) tai nuolella kirjaimen yläpuolella.

piirtääksemme vektorin käytämme sen alkioita koordinaattien arvona (X, y ja z-akseli vastaavasti). Tässä, ensimmäinen elementti (0.5) otetaan x arvo ja toinen elementti (myös, 0.5) otetaan y arvo (jos meillä oli kolme elementtiä, kolmas olisi ollut z arvo).

piirrettyämme vektorin pisteeksi laitamme siihen nuolen origosta(0,0).

vektori on yksinkertaisesti matriisi, jossa on joko yksi rivi (kutsutaan sarakevektoriksi) tai yksi sarake (kutsutaan rivivektoriksi).

matriisi

matriisi on sijoitus 2 tensori. Olemme tutkineet Matrixia aiemmin.

Tensoria, jonka arvo on suurempi kuin 2, kutsutaan yksinkertaisesti ”tensoriksi” (tensoreille, joiden arvo on yli 2, ei ole erityistä nimeä).

tensorin käsite yleistää matriisit, vektorit ja skalaarit saman katon alle (ne kaikki ovat tensoreita, mutta eri riveissä).

matriisit vektorien tulona:

kun kaksi vektoria kerrotaan, ne muodostavat matriisin.

Vector X and Y combined, have 6 elements but their product alone has 9 elements. Näin jotkut matriisit voitiin jakaa kahden vektorin tulona.