a alternative normality test is the Shapiro-Wilk test.

• mikä on Kolmogorovin-Smirnovin normaalitesti?
• SPSS Kolmogorov-Smirnov-testi NPAR-testeistä
• SPSS Kolmogorov-Smirnov-testi tutkituista muuttujista
• raportointi Kolmogorov-Smirnov-testistä
• väärät tulokset SPSS: ssä?

mikä on Kolmogorov-Smirnov-normaalitesti?

Kolmogorov-Smirnovin kokeessa tutkitaan, noudattavatko pisteet
todennäköisesti jonkinasteista jakaumaa jossain populaatiossa.Sekaannuksen välttämiseksi on olemassa 2 Kolmogorov-Smirnov-testiä:

• on yksi näyte Kolmogorov-Smirnov-testi, jolla testataan, noudattaako muuttuja tiettyä jakaumaa populaatiossa. Tämä ” annettu jakauma ”on yleensä-ei aina – normaalijakauma, joten”Kolmogorov-Smirnov-normaalijakauma”.
• on olemassa myös (paljon harvinaisempi) riippumaton otos Kolmogorov-Smirnov-testi, jolla testataan, onko muuttujalla identtiset jakaumat 2 populaatiossa.

teoriassa ”Kolmogorov-Smirnov-testi” voisi viitata jompaankumpaan testiin (mutta viittaa yleensä yhden näytteen Kolmogorov-Smirnov-testiin) ja sitä olisi parempi välttää. Muuten, molemmat Kolmogorov-Smirnov testit ovat läsnä SPSS.

Kolmogorov-Smirnov Test – yksinkertainen esimerkki

so say I ’ ve a population of 1,000,000 people. Luulen, että heidän reaktioaikansa jossain tehtävässä ovat täysin normaalisti jakautuneet. Otan näytteitä 233 näistä ihmisistä ja mittaan heidän reaktioaikansa.
Nyt näiden havaittu taajuusjakauma poikkeanee hieman – mutta ei liikaa-normaalijakaumasta. Joten ajan histogrammin Havaittujen reaktioaikojen yli ja asetan normaalijakauman samalle keskiarvolle ja keskihajonnalle. Tulos on esitetty alla.

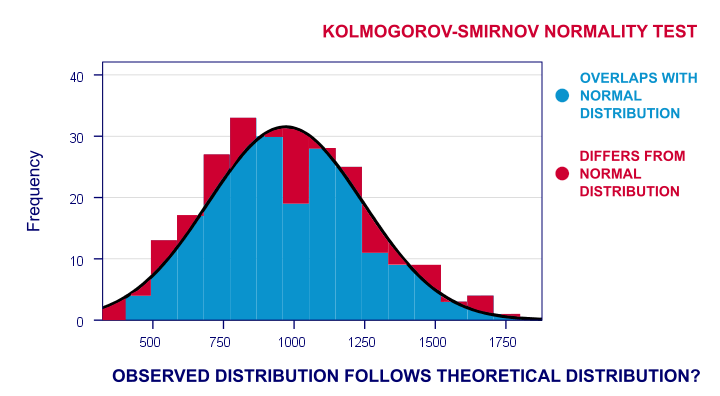
pisteideni taajuusjakauma ei mene täysin päällekkäin normaalin käyräni kanssa. Voisin laskea niiden tapausten prosenttiosuuden, jotka poikkeavat normaalista käyrästä-punaisten alueiden prosenttiosuuden kaaviossa. Tämä prosenttiluku on testitilasto: se ilmaisee yhdellä luvulla, kuinka paljon tietoni eroavat nollahypoteesistani. Se siis osoittaa, missä määrin havaitut pisteet poikkeavat normaalijakaumasta.
nyt, jos nollahypoteesini on tosi, niin tämän poikkeamaprosentin pitäisi luultavasti olla melko pieni. Toisin sanoen pienellä poikkeamalla on suuri todennäköisyysarvo tai p-arvo.
kääntäen valtava poikkeamaprosentti on hyvin epätodennäköinen ja viittaa siihen, että reaktioaikani eivät noudata normaalijakaumaa koko väestössä. Suurella poikkeamalla on siis alhainen p-arvo. Nyrkkisääntönä voidaan pitää nollahypoteesia, jos p < 0.05.So jos p < 0,05, emme usko, että muuttujamme noudattaa normaalijakaumaa väestössämme.

Kolmogorov-Smirnov Test – Test Statistic

niin se on helpoin tapa ymmärtää, miten Kolmogorov-Smirnov-normaalitesti toimii. Laskennallisesti se toimii kuitenkin eri tavalla: se vertaa havaittuja suhteessa odotettuihin kumulatiivisiin suhteellisiin frekvensseihin, kuten alla on esitetty.

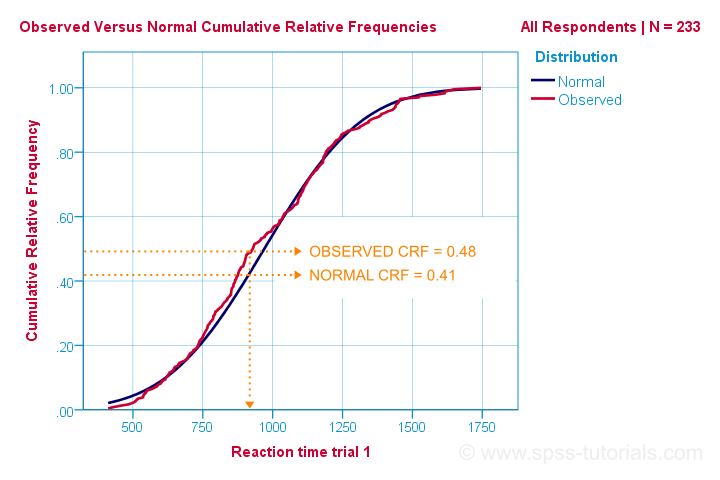
Kolmogorov-Smirnov-testi käyttää näiden käyrien suurinta absoluuttista eroa testitilastonaan D. Tässä kaaviossa suurin absoluuttinen ero d on (0, 48-0, 41 =) 0, 07 ja se tapahtuu 960 millisekunnin reaktioajalla. Muista, että D = 0.07, koska kohtaamme sen SPSS-lähdössämme minuutissa.

Kolmogorov-Smirnovin testi SPSS: ssä

on 2 tapaa suorittaa testi SPSS: ssä:

• Npar-testit sellaisina kuin ne löytyvät alta Analysis Nonparametriset testit Legacy-dialogit 1-Näytenuoli k-S… on meidän menetelmä valinta, koska se luo hienosti yksityiskohtainen tuotos.
• tutki muuttujia Analyze deskriptiivinen statistiikka Tutki on vaihtoehto. Tämä komento suorittaa sekä Kolmogorov-Smirnov-testin että Shapiro-Wilk-normaalitestin.
  Huomaa, että muuttujia tutkittaessa käytetään oletusarvoisesti listwise-poissulkemista puuttuvista arvoista. Joten jos testaan 5 muuttujaa, minun 5 testit vain käyttää tapauksia, jotka eivät ole mitään missings mitään näistä 5 muuttujia. Tämä ei yleensä ole mitä haluat, mutta näytämme miten välttää tämän.

esittelemme molemmat menetelmät speedtaskien avulla.sav kaikkialla, josta osa on esitetty alla.

tärkein tutkimuskysymyksemme on, mitkä reaktioaikamuuttujat todennäköisesti
jakautuvat normaalisti väestöömme?Nämä tiedot ovat oppikirja esimerkki siitä, miksi sinun pitäisi perusteellisesti tarkastaa tietosi ennen kuin aloitat muokkaamisen tai analysoinnin. Tehdään niin ja suoritetaan histogrammeja alla olevasta syntaksista.

tulos

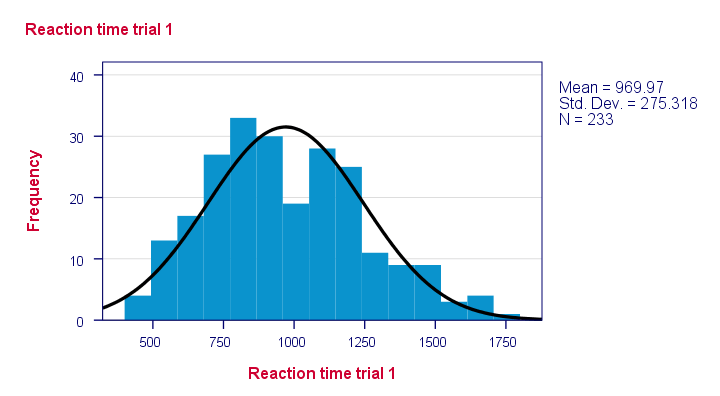
huomaa, että jotkin jakaumat eivät näytä uskottavilta lainkaan. Mutta mitkä niistä todennäköisesti jaetaan normaalisti?

SPSS Kolmogorov-Smirnovin testi NPAR-testeistä

ensisijainen vaihtoehtomme Kolmogorov-Smirnovin testin suorittamiseen on alianalysoida Nonparametriset testit Legacy Dialogs 1-näyte k-S… kuten alla.

seuraavaksi täytämme ikkunan alla esitetyllä tavalla.

liittimen klikkaaminen johtaa alla olevaan syntaksiin. Tehdään se.

Kolmogorov-Smirnov-testin syntaksi Nonparametrisista testeistä

tulokset

ensinnäkin, huomaa, että ensimmäisen muuttujan testitilasto on 0,073-aivan kuten näimme kumulatiivisessa suhteellisissa taajuuskaaviossamme hieman aiemmin. Kaaviossa on samat tiedot kuin testissämme, – joten tulokset lähentyvät mukavasti.
Tutkimuskysymyksemme osalta: vain kokeen 4 reaktioajat näyttävät jakautuvan normaalisti.

SPSS Kolmogorov-Smirnovin testi tutkittavista muuttujista

vaihtoehtoinen tapa suorittaa Kolmogorov-Smirnovin testi alkaa analysoimalla Deskriptiiviset tilastot Exploreas alla.

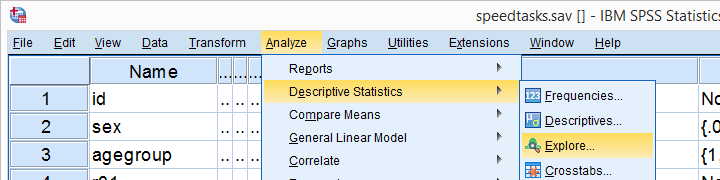
Kolmogorov-Smirnov Test Syntax from nonparametric Tests

Results

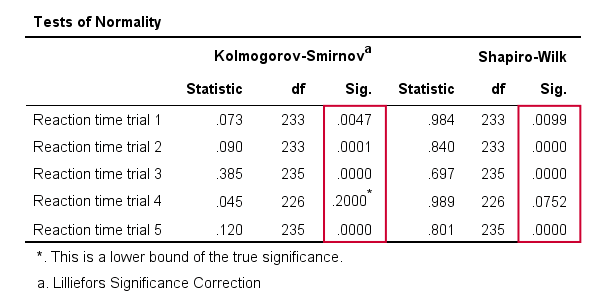
As a rule of thumb, we conclude thata variable is not normally distributed if ”Sig.” < 0.05.Sekä Kolmogorov-Smirnov-testi että Shapiro-Wilk-testitulokset viittaavat siihen, että vain Reaktioaikakoe 4 noudattaa normaalijakaumaa koko populaatiossa.
Huomaa myös, että Kolmogorovin-Smirnovin testitulokset ovat identtiset NPAR-testeistä saatujen tulosten kanssa.

Kolmogorov-Smirnov-testin raportointi

raportoidaksemme testituloksemme APA: n ohjeiden mukaisesti, kirjoitamme suunnilleen”Kolmogorov-Smirnov-testi osoittaa, että reaktioajat kokeessa 1 eivät noudata normaalijakaumaa, D(233) = 0, 07, p = 0, 005.”Lisämuuttujien osalta yritä lyhentää tätä, mutta varmista, että sisällät

• D (”erotus”), Kolmogorovin-Smirnovin testin statistiikan,
• DF, vapausasteet (joka on yhtä kuin N) ja
• P, tilastollisen merkitsevyyden.

väärät tulokset SPSS: ssä?

Jos olet opiskelija, joka haluaa vain läpäistä kokeen, voit lopettaa lukemisen nyt. Seuraa ohjeita keskustelimme tähän mennessä ja olet hyvä.

oikein, nyt ajetaan täsmälleen samat testit uudestaan SPSS: n versiossa 18 ja katsotaan lähtö.

tässä tuotoksessa on mukana tarkat p-arvot ja-onneksi – ne ovat hyvin lähellä asymptoottisia p-arvoja. Vähemmän onneksi SPSS version 18 tulokset ovat kuitenkin hurjasti erilaisia
tähän mennessä raportoiduista SPSS version 24 tuloksista.
syynä näyttää olevan lillieforsin merkitsevyyskorjaus, jota sovelletaan uudemmissa SPSS-versioissa. Tuloksena näyttää olevan, että asymptoottiset merkitsevyystasot eroavat paljon enemmän tarkasta merkityksestä kuin silloin, kun korjausta ei ole annettu ymmärtää. Tämä herättää vakavia epäilyksiä ”Lillieforsin tulosten” oikeellisuudesta-oletus uudemmissa SPSS-versioissa.
Converging evidence for this suggestion was collected by my Collector Alwin Stegeman who reran all tests in Matlab. Matlabin tulokset ovat yhtäpitäviä SPSS 18: n tulosten kanssa, eivätkä siis uudempien tulosten kanssa.

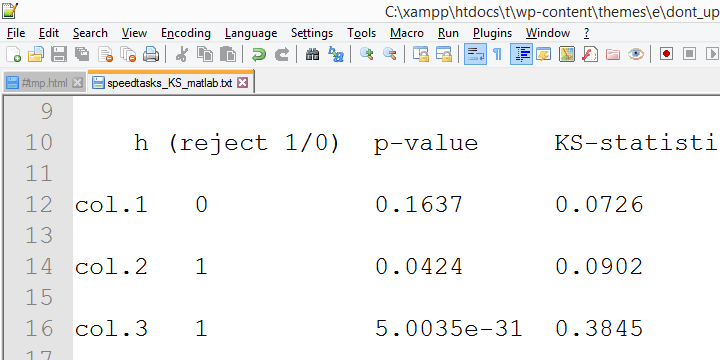
Kolmogorov – Smirnov normality test-Limited hyödyllisyys

Kolmogorov – Smirnov-testillä testataan usein monien tilastollisten testien, kuten anovan, t-testin ja monien muiden vaatimaa normaalioletusta. On kuitenkin lähes rutiininomaisesti unohdettu, että tällaiset testit ovat kestäviä tämän oletuksen rikkomista vastaan, jos otoskoot ovat kohtuullisia, sanokaamme N ≥ 25.Taustalla on keskeinen raja-arvolause. Siksi normaalisuustestejä tarvitaan vain pienille otoskooille, jos tavoitteena on täyttää normaalisuusoletus.
valitettavasti pienet otoskoot johtavat alhaiseen tilastolliseen tehoon normaalitesteissä. Tämä tarkoittaa sitä, että huomattavat poikkeamat normaalista eivät johda tilastolliseen merkitsevyyteen. Testin mukaan normaaliudesta ei ole poikettu, vaikka se on oikeasti valtava. Lyhyesti sanottuna tilanne, jossa normaalitestit ovat tarpeen-pienet otoskoot – on myös tilanne, jossa ne suoriutuvat huonosti.

Kiitos lukemisesta.