Articles

Notation de fonction et Comment Évaluer une Fonction

by admin

La notation courante d’une fonction est généralement écrite comme suit :

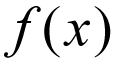
f(x) signifie que f est une expression impliquant la variable x

N’y pensez pas trop littéralement, c’est-à-dire que f est multiplié en x. Au lieu de cela, considérez ceci comme une expression mathématique qui se lit comme

f est une fonction de x

OU

f est une expression qui contient la variable ou la lettre x

Les fonctions peuvent également être écrites de différentes manières en utilisant d’autres variables telles que

div>
  • g(x), h(x) et k(x)

En outre, les fonctions peuvent prendre autres valeurs d’entrée autres que x.

  • f(a), h(r) et k(m)

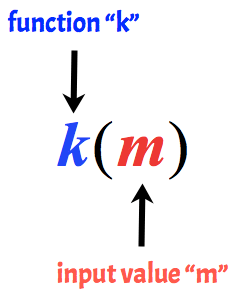
L’idée clé est toujours de se rappeler que la variable en dehors de la parenthèse est le « nom” de la fonction, tandis que la variable à l’intérieur de la parenthèse est la valeur d’entrée de la fonction.

Par exemple, ce qui suit est appelé fonction k avec une valeur d’entrée de m.

k(m) peut être lu comme la fonction de k de m. cela signifie que la fonction k est exprimée en termes de m puisque m est la valeur d'entrée.

Exemples de base de fonctions d’évaluation

Exemple 1: Évaluez la fonction.

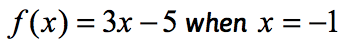
f(x) = 3x-5 lorsque x =-1

C’est la notation normale de la fonction où la fonction est f alors que la valeur d’entrée est x. Pour évaluer une fonction, ce que nous voulons, c’est substituer à chaque fonction exemple de x dans l’expression, puis simplifiez.

Depuis x=-1, on remplace cette valeur dans la fonction et on simplifie. Ce faisant, nous obtenons une solution qui ressemble à ceci.

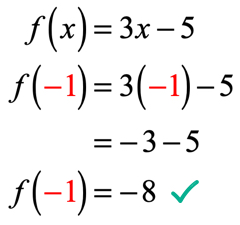
f(x)=3x-1 → f(-1) = 3(-1) - 5 → f(-1) = -3 -5 = -8. par conséquent, f(-1) = -8.

Exemple 2 : Évaluez la fonction.

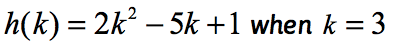
h(k) = 2k^2-5k +1 lorsque k = 3

Observez que la fonction ici est h et que la valeur d’entrée est k. Tout comme dans notre exemple précédent, nous voulons substituer quelle que soit la valeur numérique attribuée à k dans la fonction donnée, et simplifier.

Puisque k =3, votre solution devrait ressembler à ceci

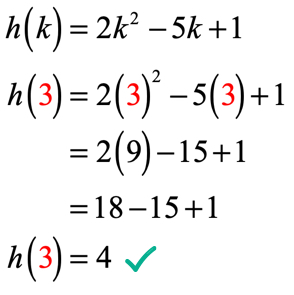
h(k)=2k^2-5k +1 →h(3) = 2(3)^2 - 5(3) + 1 → d(3) = 2(9) -15+1 → d(3) = 18 - 15 + 1 → h(3) = 4.

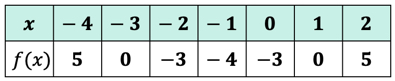
Exemple 3: Évaluez chaque valeur de x dans le tableau ci-dessous en utilisant la fonction ci-dessous. Tracez les points dans l’axe xy et reliez les points pour révéler le graphique de la fonction.

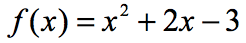
f(x) = x^2 + 2x-3

une table de valeurs pour la fonction f de x ou f(x) où les valeurs x sont -4, -3, -2, -1, 0, 1 et 2

Puisqu’il y a sept entrées x, cela signifie que nous évaluerons également la fonction sept fois. Essayez de résoudre ce problème par vous-même, puis revenez vérifier vos réponses.

Si vous l’avez fait correctement, ce sont les valeurs:

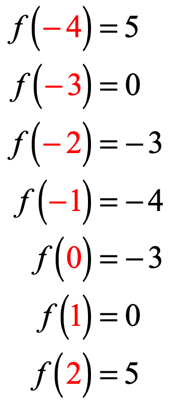
ce sont les valeurs de la fonction lorsqu'elles sont évaluées avec chaque valeur x ou valeur d'entrée. f(-4) = 5, f(-3) = 0, f(-2) = -3, f(-1) =-4, f(0) = -3, f(1) = 0, f(2) = 5.

Nous pouvons maintenant placer ces valeurs de sortie dans la table.

voici le tableau complet des valeurs représentées par un ensemble de paires ordonnées: { (-4,5), (-3,0), (-2,-3), (-1,-4), (0,-3), (1,0), (2,5) }

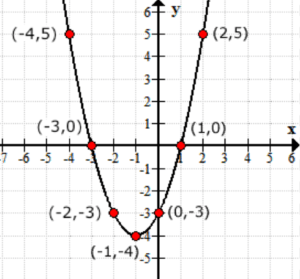
Considérez les valeurs de sortie de la fonction f\left(x\right) comme les valeurs y. Voici à quoi ressemble le graphique sur l’axe xy.

après avoir tracé les points de la table générée par la fonction f(x) = x^2 + 2x -3, nous obtenons une parabole qui s'ouvre avec un minimum à (-1, -4), l'ordonnée à l'origine de -3 et x-interceptions de -3 et 1.

Exemples intermédiaires de Fonctions d’évaluation

Exemple 4: Étant donné que g\left(x\right) = {x^2}-3x+1, trouvez g\left({2x-1}\right).

Dans les exemples précédents, nous avons évalué une fonction par un nombre. Cette fois, la valeur d’entrée n’est plus une valeur numérique fixe, mais une expression. Cela peut sembler compliqué mais la procédure reste la même.

Nous remplacerons chaque instance de x dans g\left (x\right) par la valeur d’entrée qui est 2x-1. Simplifiez en mettant au carré le binôme, en appliquant la propriété distributive et en combinant des termes similaires.

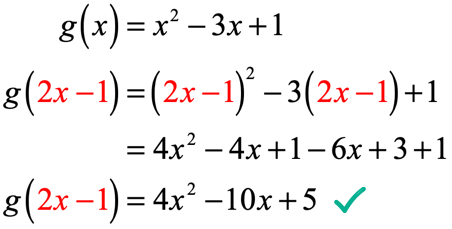
g(x) = x^2-3x+1 →g(2x-1) =(2x-1) ^2-3(2x-1) +1 →g(2x-1) =4x ^2-4x + 1 - 6x +3 = 1 →g(2x-1) = 4x^2-10x + 5

Exemple 5: Étant donné que p\left(x\right) = {{4x-1}\over x}, évaluez p\left(1\right) – p\left({-1}\right).

Le problème peut sembler intimidant au début, mais une fois que nous l’analysons et appliquons ce que nous savons déjà sur la façon d’évaluer les fonctions, cela ne devrait pas être si grave!

Ce que nous devons faire ici est d’évaluer la fonction à x = 1 puis de la soustraire par la valeur de la fonction lorsqu’elle est évaluée à x =-\, 1.

Soyez très prudent lorsque vous remplacez les valeurs et pendant le processus de simplification. Si vous ne faites pas attention à chaque étape, il est très facile de commettre des erreurs lorsque vous ajoutez, soustrayez, multipliez ou divisez des nombres positifs et négatifs.

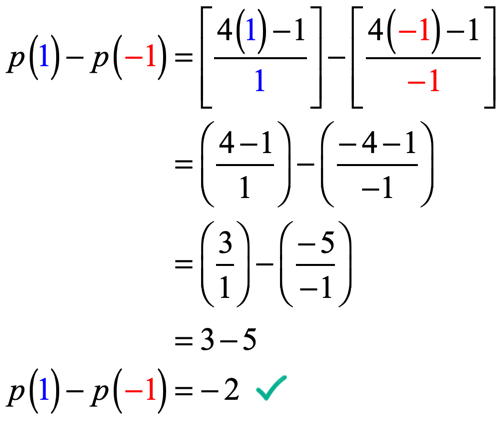
p(1)-p(-1) = { /(1) } - { /(-1) } = - = 3-5 → p(1) - p(-1) = -2

Exemple avancé d’Application du Concept d’évaluation des fonctions

Exemple 6: Si f\left(2\right) = 9, trouvez la valeur de a dans la fonction ci-dessous.

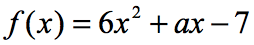
f(x) = 6x^2 + ax-7, trouvez la valeur de a

Dans l’équation, f\left(2\right) = 9, on nous dit que si l’entrée de la la fonction est 2; la sortie de la fonction sera 9. Puisque la fonction nous est donnée, notre premier geste consiste à au moins remplacer la valeur de 2, puis à simplifier. C’est ce que nous aurons.

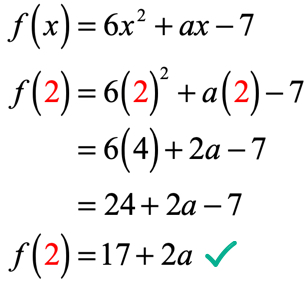
f(x) =6x^2 + ax-7 →f(2) = 6(2)^2 + a(2)-7 → f(2) = 6(4) + 2a-7 = 24 + 2a-7 → f(2) = 17 + 2a

La sortie de la fonction après évaluation à x = 2 est 17 + 2a. Rappelez-vous, on nous dit également que la sortie est 9 en utilisant l’équation donnée f \ left (2 \right) = 9. Par conséquent, ce que nous devons faire maintenant, c’est les mettre égaux les uns aux autres et résoudre l’équation linéaire pour la valeur inconnue de a.

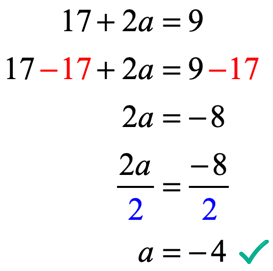
17 +2a= 9 → 17-17 + 2a= 9-17 → 2a= -8 →(2a) / 2 = -8/2 → a = -4

Vérifions si la valeur de a =-\, 4 dans f(x) = 6 {x^2} + ax-7 peut faire de la condition donnée f\left(2\right) = 9 une déclaration vraie.

f(x) =6x^2-4x-7 →f(2) = 6(2)^2 - 4(2) - 7 = 6(4) - 8- 7 = 24 - 8 - 7 → f(2) =9

C’est vrai! Par conséquent, nous avons résolu avec succès la valeur correcte de a.