En parlant de fiabilité, parallèle, signifie que l’un des éléments de la structure parallèle permet au système de fonctionner. Cela ne signifie pas qu’ils sont physiquement parallèles (dans tous les cas), car les condensateurs en parallèle fournissent un comportement spécifique dans le circuit et si un condensateur tombe en panne, ce système pourrait tomber en panne.
Dans ce dessin simple, il y a n composants en parallèle et n’importe quel composant est nécessaire pour que le système fonctionne.

Si le composant #2 échoue, les autres permettront au système de fonctionner.

Simple. Et, très utile. Cette construction permet d’améliorer globalement la fiabilité, même au-delà de la fiabilité des composants individuels. Contrairement aux systèmes en série où le composant le plus faible limite la fiabilité, ici, en ajoutant de la redondance, la fiabilité du système s’améliore.

Considérons un système parallèle à deux composants. Si les deux composants fonctionnent tous les deux, le système fonctionne. Si le composant 1 ou 2 tombe en panne, le système fonctionne toujours. Si et seulement si les deux composants échouent, le système échoue. Contrairement à un système en série où une défaillance entraîne une défaillance du système, dans cet exemple simple, deux événements de défaillance doivent se produire avant que le système ne tombe en panne.

Quelle est la chance d’avoir deux échecs? La formule est basée sur la probabilité que le composant 1 ou le composant 2 fonctionne. Sans faire la dérivation, nous pouvons écrire la fiabilité du système parallèle à 2 composants comme suit:

Ceci est très compliqué rapidement avec plus de trois composants en parallèle. Avant d’explorer une autre façon de calculer des systèmes parallèles, il y a une situation de cas particulier à mentionner en premier.

Lorsque les composants en parallèle sont les mêmes (en termes de fiabilité), alors ce qui précède se simplifie en

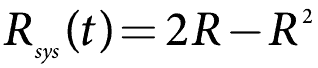
Ce qui devrait être évident.

Il est souvent plus facile de faire des calculs de système parallèles en utilisant le manque de fiabilité, ou 1–R(t). C’est aussi le CDF ou F(t). Le calcul est maintenant plus comme un système de série avec une correction. Pour le cas général, la formule de fiabilité du système pour un système parallèle devient

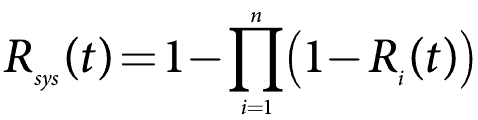
Donc, disons que nous avons cinq composants avec fiabilité à un an d’utilisation, R(1), à 90%, ou 0,9. Calculez la fiabilité du système.

En utilisant la formule ci-dessus et en définissant la fiabilité de chaque élément à 0,9, on trouve

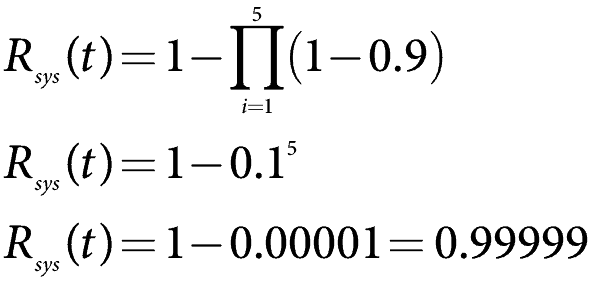
qui est très fiable.

Il est coûteux d’ajouter des pièces redondantes à un système, mais dans certains cas, c’est la bonne solution pour créer un système qui répond aux exigences de fiabilité. Bien sûr, les systèmes réels présentent de nombreuses variations et complications par rapport à la simple configuration des composants en parallèle. Le partage de charge, la veille chaude, chaude ou froide, les systèmes de commutation ou de vote, et bien d’autres peuvent compliquer la construction d’un système parallèle.

L’utilisation de composants en parallèle est le seul moyen d’augmenter la fiabilité du système au-delà des limites de fiabilité des composants individuels.

Connexes:

Présentation des diagrammes de blocs de fiabilité et valeur (article)

Répartition de la fiabilité (article)

k sur n (article)