egy tenzor egy adatsor (számok, függvények stb.), amely a méretek tetszőleges számában (0 vagy annál nagyobb) bővül. A méretek számát tenzor rangnak nevezik.

Rank 0 tensor

egy tenzor, amelynek nincs mérete (0).

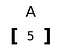
rank 1 tensor

egy tenzor, amely csak egy dimenzióban bővül.

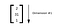
Rank 2 tensor

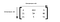
Rank 3 tensor

As shown in figure, a rank 3 tensor has a cube (or cuboid like structure).

If rank of a tensor exceeds 3, it becomes difficult to visualize.

skalár

a skalár 0 rank tensor. A fizikában különböző mennyiségeket ábrázolnak skalárként, például: távolság (500 km), hőmérséklet (10ºC), sebesség (34 km/h) stb.

Vektor

a rang 1 tenzor nevezzük vektor. Fizikai mennyiségek, például sebesség (10 m/s), elmozdulás (54 m kelet felé), elektromágneses mező (1 V/m).

különbség a skalár és a vektor között :

egy olyan mennyiség, amely nem igényel további információkat (például irányt) vele (például hőmérsékletet), skalárként jelenik meg. Míg egy olyan mennyiséget, amelyet a nagysága mellett meg kell határozni, vektorral (például elektromos mezővel) ábrázolnak.

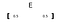
a vektort félkövér betűvel (például “e” ) vagy a betű feletti nyíl jelöli.

egy vektor ábrázolásához az elemeit használjuk koordináták értékeként (x, y, illetve z tengely). Itt az első elemet (0,5) x értéknek vesszük, a második elemet (szintén 0,5) pedig y értéknek (ha három elemünk lenne, a harmadik z érték lett volna).

miután a vektort pontként ábrázoltuk, egy nyilat helyezünk rá, származásból(0,0).

a vektor egyszerűen egy mátrix, amely egy sorral (úgynevezett oszlopvektorral) vagy egy oszlopgal (úgynevezett sorvektorral) rendelkezik.

Matrix

a Mátrix egy rank 2 tenzor. Korábban megnéztük a matrix-ot.

a 2-nél nagyobb rangú tenzort egyszerűen “tensor” – nak nevezik (a 2-nél nagyobb rangú tenzorok esetében nincs konkrét név).

a tenzor fogalma általánosítja a mátrixokat, vektorokat és skalárokat egy fedél alatt(mindegyik tenzor, de különböző sorokkal).

mátrixok a vektorok termékeként:

amikor két vektort megszoroznak, mátrixot alkotnak.

Vector X and Y combined, have 6 elements but their product alone has 9 elements. Így néhány mátrixot két vektor termékeként lehet lebontani.