A Cobb-Douglas termelési funkció
hirdetések:
az alább említett cikk szoros képet nyújt a Cobb-Douglas termelési funkcióról.
A Cobb-Douglas termelési funkció Paul H. Douglas és C. W. Cobb által készített amerikai feldolgozóipar empirikus tanulmányán alapul. Ez egy lineáris homogén termelési függvény az első fok, amely figyelembe veszi a két bemenet, a munkaerő és a tőke, a teljes kimeneti .feldolgozóipar.
A Cobb-Douglas termelési függvényt a következőképpen fejezzük ki:
Q = ALa Cß
ahol Q is output, l pedig С a munkaerő és a tőke inputja. Egy, egy, illetve β pozitív paraméterek hol = > O, β > O.
Az egyenlet azt mondja, hogy a kimenet közvetlenül függ, L, C, s, hogy része kimenet, ami nem magyarázható a L С azzal magyarázható, amely a “maradék”, gyakran az úgynevezett technikai változás.
A termelési függvény megoldani a Cobb-Douglas volt, 1/4 hozzájárulás a tőke a növekedés a feldolgozóipar, valamint a 3/4 munkaerő, így a C-D termelési függvény
REKLÁMOK:
Q = AL3/4 C1/4
ami azt mutatja, állandó visszatér a skála, mert a teljes érték a L С egyenlő: (3/4 + 1/4), azaz(a + β = 1) . A C-D függvényben a labourer együtthatója méri a százalékos növekedést (Q, amely az L 1 százalékos emelkedéséből származna, miközben a С-t állandónak tartja.
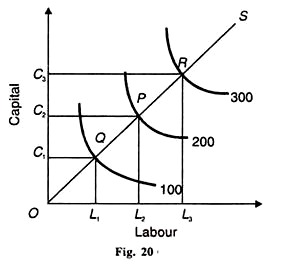
Hasonlóképpen, a В A Q százalékos növekedése, amely a C 1% – os növekedéséből származna, miközben az L-T állandónak tartja. A C-D termelési függvény, amely állandó visszatérést mutat a skálára, a 20. ábrán látható. A munkaerő-bevitel a vízszintes tengelyen, a tőke pedig a függőleges tengelyen történik.
100 egységnyi termelés előállításához az ОС, a tőkeegységeket és az OL munkaegységeket használják. Ha a kibocsátás megduplázódna 200-ra, a munkaerő és a tőke ráfordításait meg kellene duplázni. Az ОС pontosan kétszerese az ОС1-nek, az OL2 pedig az OL2-nek.
Az OC3 és az OL3 háromszor nagyobb, mint az ОС1, illetve az OL1. Egy másik módszer a Q, P és R egyensúlyi pontokat összekötő skálavonal vagy tágulási út.
Ez azt mutatja, hogy az isoquants 100, 200 és 300 egyenlő távolságra van. Így az OQ = QP = PR OS skálán, amely azt mutatja, hogy ha a tőke és a munkaerő egyenlő arányban növekszik, akkor a kibocsátás is azonos arányban növekszik.
A C-D termelési funkció kritikája:
A C-D termelési funkciót az Arrow, Chenery, Minhas és Solow kritizálta az alábbiak szerint:
1. A C – D termelési funkció csak két inputot, a munkaerőt és a tőkét veszi figyelembe, és figyelmen kívül hagy néhány fontos inputot, például a termelésben felhasznált nyersanyagokat. Ezért nem lehet ezt a funkciót több mint két bemenetre általánosítani.
2. A C-D termelési funkcióban a tőke mérésének problémája azért merül fel, mert csak a termeléshez rendelkezésre álló tőke mennyiségét veszi igénybe. De a rendelkezésre álló tőke teljes felhasználása csak a teljes foglalkoztatás időszakában lehetséges. Ez irreális, mert egyetlen gazdaság sem mindig teljes mértékben foglalkoztat.
3. A C-D termelési funkciót kritizálják, mert állandó visszatérést mutat a skálára. De a skála állandó visszatérése nem aktualitás, mivel a növekvő vagy csökkenő visszatérések a termelésre alkalmazhatók.
nem lehetséges az összes bemenet megváltoztatása az összes iparág kimeneteinek arányos változása érdekében. Egyes inputok szűkösek, és nem növelhető ugyanolyan arányban, mint a bőséges inputok. Másrészt olyan bemenetek, mint a gépek, a vállalkozói szellem stb. oszthatatlanok. Mivel a kibocsátás növekszik az oszthatatlan tényezők maximális kapacitásuk miatt, az egységköltség csökken.
:
így ha a bemenetek ellátása szűkös és oszthatatlan, akkor a skála állandó visszatérése nem lehetséges. Amikor a termelési folyamat során a különböző inputok egységei növekednek, a méretgazdaságosság és a specializáció egyre nagyobb mértékű visszatérést eredményez.
a gyakorlatban azonban egyetlen vállalkozó sem szeretné növelni a különböző bemeneti egységeket a kibocsátás arányos növekedése érdekében. Arra törekszik, hogy több mint arányosan növekedjen a kibocsátás, bár a csökkenő hozamok sem zárhatók ki.
4. A C-D termelési funkció a tényezők helyettesíthetőségének feltételezésén alapul, figyelmen kívül hagyja a tényezők komplementaritását.
5. Ez a funkció azon a feltételezésen alapul, hogy a faktorpiacon tökéletes a verseny, ami irreális. Ha azonban ez a feltételezés csökken, az α És β együtthatók nem jelentenek faktorrészeket.
hirdetések:
6. A C-D funkció egyik gyengesége az aggregációs probléma. Ez a probléma akkor merül fel, amikor ezt a funkciót egy iparág minden cégére és az egész iparágra alkalmazzák. Ebben a helyzetben az alacsony vagy magas aggregáció számos termelési funkciója lesz. Így a C-D funkció nem méri azt, amit mérni kíván.
következtetés:
így a C-D gyártási funkció kivitelezhetősége a feldolgozóiparban kétséges. Ez nem vonatkozik a mezőgazdaságra, ahol az intenzív termesztés érdekében az inputmennyiségek növelése nem növeli a kibocsátást arányosan. Még akkor sem tagadható, hogy az állandó visszatérések a méretekben egy vállalkozás, ipar vagy gazdaság életének egy szakasza. Egy másik dolog, hogy ez a szakasz egy idő után, rövid ideig jöhet.
fontos:
hirdetések:
a kritikák ellenére a C-D funkció nagyon fontos.
1. Széles körben használják a feldolgozóipar empirikus tanulmányaiban, valamint az iparágak közötti összehasonlításokban.
2. Ezt használják a munkaerő és a tőke relatív részesedésének meghatározására a teljes kibocsátásban.
3. Euler tételének bizonyítására használják.
4. Az A és b paraméterei az ágazatközi összehasonlításokhoz használt rugalmassági együtthatókat képviselik.
5. Ez a termelési függvény lineáris homogén mértéke, amely azt mutatja, állandó visszatér a skála, Ha α + β = 1, egyre több visszatér a mérleg, ha α + β < 1, akkor ott vannak a csökkenő hozadék, hogy a skála.
hirdetések:
6. A közgazdászok ezt a termelési funkciót több mint két változóra kiterjesztették.
Leave a Reply