Funkció Jelölés, illetve Hogyan Értékeli a Funkció
A közös jelölés a funkció általában írva, mint,
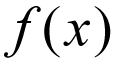
ez nem is szó szerint, hogy f az, hogy meg kell szorozni, hogy x-et. Ehelyett ezt matematikai kifejezésnek kell tekinteni, amelyet

vagy

a függvényeket más változókkal is meg lehet írni, például
- g(x), H(X) és K(x)
ezenkívül a funkciók x.
- F(a), h(r) és k(M)
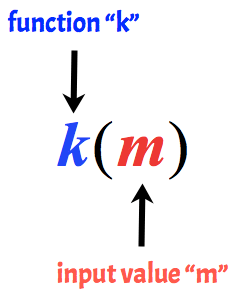
a kulcsgondolat mindig emlékezni kell arra, hogy a zárójelen kívüli változó a függvény “neve”, míg a zárójelen belüli változó a zárójelben lévő érték bemeneti értéke.a funkció.
például a következőket nevezik k függvénynek, amelynek bemeneti értéke m.
alapvető példák a funkciók értékelésére
példa 1: értékelje a funkciót .
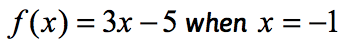
Ez a függvény normál jelölése, ahol a függvény f, míg a bemeneti érték x. egy függvény kiértékeléséhez azt szeretnénk, hogy cserélje ki az X minden példányát a kifejezésben, majd egyszerűsítse.
mivel x = – 1, helyettesítjük ezt az értéket a függvényben, egyszerűsítjük. Ennek során olyan megoldást kapunk, amely így néz ki.
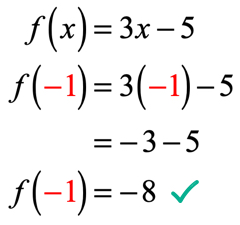
2. példa: értékelje a függvényt .
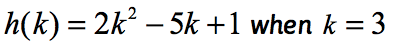
vegye figyelembe, hogy a függvény itt h, a bemeneti érték pedig k. Csakúgy, mint az előző példánkban, azt akarjuk, hogy az adott függvényben a K-hez rendelt számértéket helyettesítsük, egyszerűsítsük.
Mivel k = 3, a megoldást kell keresni, ehhez hasonló
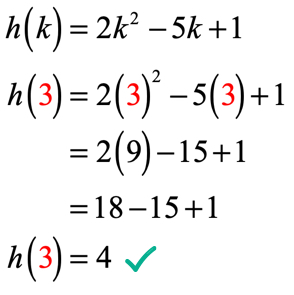
3. példa: értékelje az alábbi táblázatban szereplő X minden értékét az alábbi funkció segítségével. Rajzolja meg az XY tengely pontjait, majd csatlakoztassa a pontokat, hogy felfedje a függvény grafikonját.
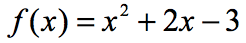

Mivel a heten vannak az x-bemenetek, ami azt jelenti, hogy a függvény kiértékelése hétszer is. Próbáld ki ezt a saját, majd gyere vissza, hogy ellenőrizze a válaszokat.
ha helyesen tette, ezek az értékek:
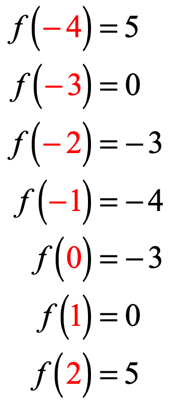
ezeket a kimeneti értékeket most elhelyezhetjük a táblázatban.
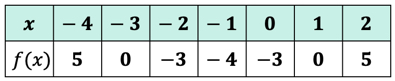
Gondolj az F\left( x \right) függvény kimeneti értékeire y-értékként. Így néz ki a grafikon az xy tengelyen.
közbenső példák a funkciók értékelésére
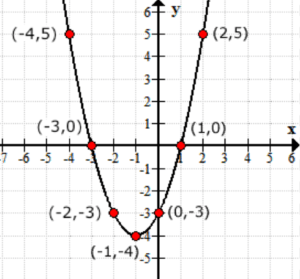
4. példa: tekintettel arra, hogy g \ bal (x \ jobb) = {x^2} – 3x + 1, Keresse meg a G\bal( {2x – 1} \jobb).
az előző példákban egy függvényt szám szerint értékeltünk. Ezúttal a bemeneti érték már nem rögzített numerikus érték, hanem kifejezés. Bonyolultnak tűnhet, de az eljárás ugyanaz marad.
az x minden példányát g\balra( x \jobbra) cseréljük a 2x – 1 bemeneti értékkel. Egyszerűsítse a binomiális négyzetet, alkalmazza az elosztó tulajdonságot és kombinálja a hasonló kifejezéseket.
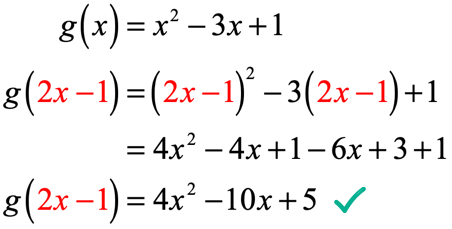
5. Példa: Adott, hogy a p\left( x \jobbra) = {{4x – 1} \over x} , értékelése, p\left( 1 \jobbra) – p\left( { – 1} \right).
a probléma először félelmetesnek tűnhet, de ha egyszer elemezzük, és alkalmazzuk azt, amit már tudunk a funkciók értékeléséről, ez nem lehet olyan rossz!
itt azt kell tennünk,hogy értékeljük a függvényt x = 1 – nél, majd kivonjuk a függvény értékével, ha x= -\, 1-nél értékeljük.
legyen nagyon óvatos az értékek helyettesítésekor és az egyszerűsítési folyamat során. Ha nem vagy óvatos minden lépésben, nagyon könnyű hibákat elkövetni, ha pozitív és negatív számokat adsz hozzá,vonszol, szorozol vagy osztasz.
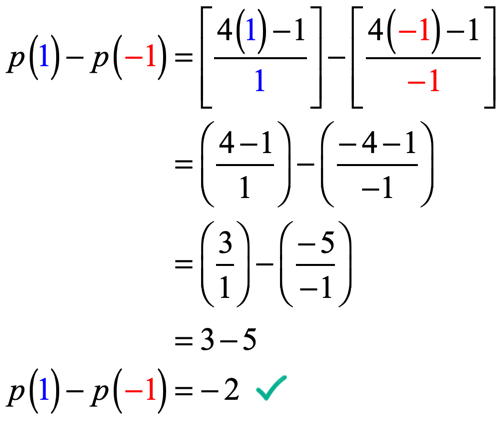
Speciális Példa Fogalmának Alkalmazása Értékelő Függvények
6. Példa: Ha az f\left( 2 \jobbra) = 9, megtalálni az értéket a függvény alatt.
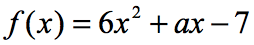
az egyenletben, f\bal( 2 \jobb) = 9, azt mondják, hogy ha a bemenet a funkció 2; a funkció kimenete 9 lesz. Mivel a funkciót nekünk adják, az első lépés az, hogy legalább helyettesítsük a 2 értéket,majd egyszerűsítsük. Ezt fogjuk kapni.
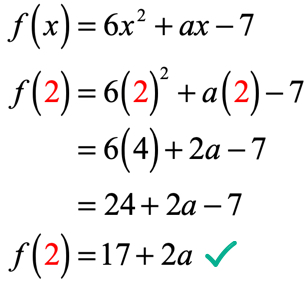
a függvény kimenete az X = 2 értékelése után 17 + 2a. ne feledje, hogy a kimenet 9 az f\left( 2 \right) = 9 egyenlet használatával. Ezért az, amit tennünk kell, most van állítva őket egyenlő egymással, majd oldja meg a lineáris egyenlet az ismeretlen értékét.
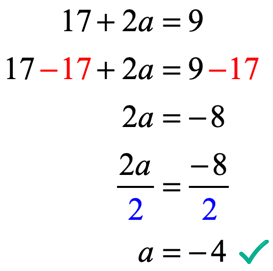
nézzük, ellenőrizze, hogy az érték a = – \,4 f(x) = 6{x^2} + ax – 7 lehet, hogy az adott feltétel f\left( 2 \jobbra) = 9 lenni egy igaz kijelentés.

Ez igaz! Ezért sikeresen megoldottuk az a.
helyes értékét
Leave a Reply