Michael Hartley

a bűvös négyzet egy rács, amely tartalmazza az 1, 2, 3 stb.számokat, ahol minden sor, oszlop és átló ugyanazt a számot adja. Egy példa az alábbiakban látható, látni fogja, hogy minden sor, oszlop és átlós összeadódik akár 34. Ez a 34-es szám a mágikus tér “mágikus száma”.

a mágikus négyzetek megtalálása vagy a mágikus négyzet rejtvények megoldása sokkal könnyebb, ha ismeri a mágikus számot. A jó hír az, hogy miután megismerte a kívánt mágikus négyzet méretét, kiszámíthatja a mágikus számot anélkül, hogy túl sok baj lenne. Ennek oka egy csodálatos tény :

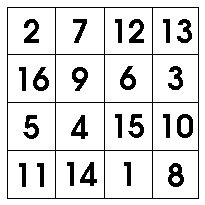
• a mágikus szám csak a négyzetrács méretétől függ, nem attól,hogy a számok hogyan vannak elrendezve benne

miért van ez? Tegyük fel, hogy összeadod a mágikus négyzet minden sorát. Minden sor hozzáadja a mágikus számot. Tehát, ha összeadja az összes cellát, annyiszor adta hozzá ezt a mágikus számot, ahányszor sorok vannak a rácsban. Jegyezzük meg ezt a tényt:

• a rács összes cellájának összege a

sorok számának mágikus száma, de van egy másik módja annak, hogy az összes cellát összeadjuk, mivel minden 1., 2., 3. szám és így tovább pontosan egyszer jelenik meg. A rács legnagyobb száma az oszlopok számának szorzata. Ezért

• a rács összes cellájának összege az összes szám összege 1-től az oszlopok számának szorosáig.

a mágikus négyzetnek ugyanannyi sora van, mint az oszlopoknak, így a mágikus szám csak a mágikus négyzet sorainak számától függ. A következő lépések segítenek megoldani:

• vegye be a sorok számát, majd szorozza meg ezt önmagában
• adjon hozzá egy
• ismét szorozza meg a sorok számát.
• oszd meg két

például a négy négy négyzet felett (vagy bármely négy négy négy mágikus négyzet), a mágikus szám lehet kidolgozni, mint:

• négyszer négy 16,
• add one, ad 17
• szorozzuk újra négy, ad 68
• oszd meg két, ad 34!

néhány számítás mentése érdekében néhány különböző méretű mágikus négyzet mágikus számát adtam az alábbiakban:

• egy 3 x 3 négyzet esetében a mágikus szám 15.
• egy 4 által 4 négyzet, a mágikus szám 34.
• egy 5 által 5 négyzet, a mágikus szám 65.
• egy 6 által 6 négyzet, a mágikus szám 111.
• egy 7 által 7 négyzet, a mágikus szám 175.
• egy 8 által 8 négyzet, a mágikus szám 260.
• egy 9 által 9 négyzet, a mágikus szám 369.
• egy 10 által 10 négyzet, a mágikus szám 505.

a tiéd, Dr. Mike!