egy alternatív normalitás teszt a Shapiro-Wilk teszt.

• mi a Kolmogorov-Smirnov normalitási teszt?
• SPSS Kolmogorov-Smirnov test from NPAR TESTS
• SPSS Kolmogorov-Smirnov test from EXAMINATE változók
• Kolmogorov-Smirnov Test
• hibás eredmények az SPSS-ben?

mi a Kolmogorov-Smirnov normality teszt?

a Kolmogorov-Smirnov teszt azt vizsgálja, hogy a
pontszámok valószínűleg bizonyos populációban bizonyos eloszlást követnek-e.Az összetévesztés elkerülése érdekében 2 Kolmogorov-Smirnov teszt van:

• ott van az Egy minta Kolmogorov-Smirnov teszt annak tesztelésére, hogy egy változó egy adott eloszlást követ-e egy populációban. Ez az” adott Eloszlás “általában-nem mindig – a normál eloszlás, ezért”Kolmogorov-Smirnov normalitás teszt”.
• ott van még a (sokkal kevésbé gyakori) független minták Kolmogorov-Smirnov teszt annak vizsgálatára, hogy egy változó azonos eloszlású-e 2 populációban.

elméletileg a “Kolmogorov-Smirnov-teszt”bármelyik tesztre utalhat (de általában az Egymintás Kolmogorov-Smirnov-tesztre utal), és jobb elkerülni. By the way, mindkét Kolmogorov-Smirnov teszt jelen van az SPSS-ben.

Kolmogorov-Smirnov teszt-egyszerű példa

tehát azt mondják, hogy 1 000 000 ember lakossága van. Úgy gondolom, hogy a reakcióidők valamilyen feladatra tökéletesen eloszlanak. Ezek közül 233-at mintavételezek, és megmérem a reakcióidőket.
Most ezeknek a megfigyelt frekvenciaeloszlása valószínűleg kissé eltér – de nem túl sok-a normál eloszlástól. Tehát lefuttatok egy hisztogramot a megfigyelt reakcióidőn keresztül, és egy normál eloszlást helyezek egybe ugyanazzal az átlagos és szórással. Az eredmény az alábbiakban látható.

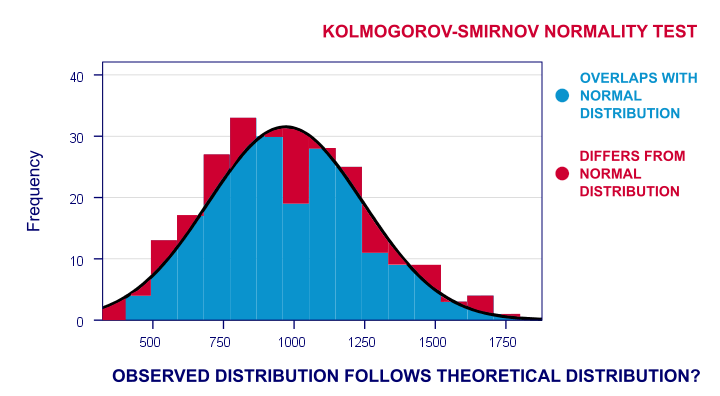
a pontszámaim frekvenciaeloszlása nem teljesen átfedésben van a normál görbémmel. Most kiszámolhatom az esetek százalékos arányát, amelyek eltérnek a normál görbétől-a diagram vörös területeinek százalékos arányát. Ez a százalék egy tesztstatisztika: egyetlen számban fejezi ki, hogy az adataim mennyire különböznek a null hipotézisemtől. Tehát azt jelzi, hogy a megfigyelt pontszámok milyen mértékben térnek el a normál eloszlástól.
most, ha a null hipotézisem igaz, akkor ennek az eltérési százaléknak valószínűleg elég kicsinek kell lennie. Vagyis egy kis eltérés nagy valószínűségi értékkel vagy p-értékkel rendelkezik.
fordítottan, egy hatalmas eltérés százalék nagyon valószínűtlen, és azt sugallja, hogy a reakcióidőm nem követi a normális eloszlást az egész populációban. Tehát egy nagy eltérésnek alacsony p-értéke van. Hüvelykujjszabályként a nullhipotézist vetették fel, ha p < 0.05.So ha p < 0, 05, akkor nem hisszük, hogy változónk normális eloszlást követ a lakosságban.

Kolmogorov-Smirnov Tesztstatisztika

tehát ez a legegyszerűbb módja annak, hogy megértsük, hogyan működik a Kolmogorov-Smirnov normalitás teszt. Számítási szempontból azonban másképp működik: összehasonlítja a megfigyelt értéket a várható halmozott relatív frekvenciákkal szemben, az alábbiak szerint.

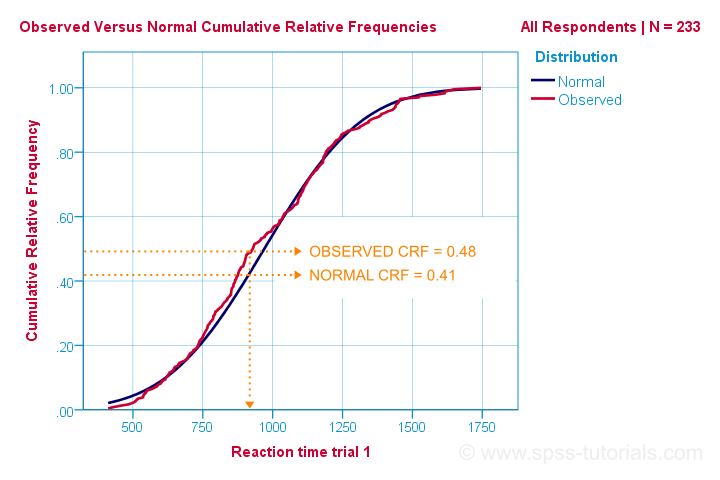
A Kolmogorov-Szmirnov teszt használ a maximális abszolút különbség a között, hogy ezek a görbék, mint a vizsgálati statisztika jelöli D. ez A diagram, a maximális abszolút különbség D (0.48 – 0.41 =) 0.07 ez akkor fordul elő, a reakció idő 960 milliszekundum. Ne feledje, hogy D = 0,07, mivel egy perc alatt találkozunk vele az SPSS kimenetünkben.

A Kolmogorov-Smirnov teszt SPSS-ben

a teszt futtatásának 2 módja van SPSS-ben:

• NPAR tesztek az Analyze Nonparametric Tests Legacy Dialogs 1-Sample K-S… a mi választott módszerünk, mert szépen részletes kimenetet hoz létre.
• vizsgálja változók elemzése leíró statisztikák Explore egy alternatíva. Ez a parancs mind a Kolmogorov-Smirnov tesztet, mind a Shapiro-Wilk normality tesztet futtatja.
  vegye figyelembe, hogy a változók vizsgálata alapértelmezés szerint a hiányzó értékek listás kizárását használja. Tehát, ha 5 változót tesztelek, az én 5 tesztem csak olyan eseteket használ, amelyekben nincs hiba ezen 5 változón. Ez általában nem az, amit akarsz, de megmutatjuk, hogyan lehet ezt elkerülni.

mindkét módszert speedtasks használatával mutatjuk be.sav egész, amelynek egy része az alábbiakban látható.

fő kutatási kérdésünkmelyik a reakcióidő változók valószínűleg
hogy általában eloszlik a lakosság?Ezek az adatok tankönyvi példa arra, hogy miért kell alaposan megvizsgálnia adatait a Szerkesztés vagy elemzés megkezdése előtt. Csináljunk csak, és futtassunk le néhány hisztogramot az alábbi szintaxisból.

eredmény

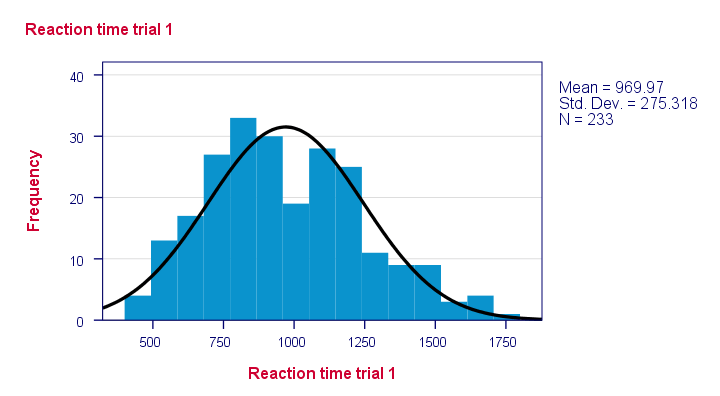
vegye figyelembe, hogy egyes eloszlások egyáltalán nem tűnnek valószínűnek. De melyiket valószínűleg általában elosztják?

SPSS Kolmogorov-Szmirnov teszt a NPAR VIZSGÁLATOK

A kívánt opciót a futó a Kolmogorov-Szmirnov teszt underAnalyze Nemparaméteres Vizsgálatokat Legacy Párbeszédek 1-Minta K-S… amint az alább látható.

ezután csak töltse ki a párbeszédpanelt az alábbiak szerint.

kattintva beillesztés eredmények a szintaxis alatt. Futtassuk le.

Kolmogorov-Smirnov teszt szintaxis Nemparametrikus tesztekből

Eredmények

Először, vegye figyelembe, hogy a vizsgálati statisztika az első változó 0.073 -mint láttuk, a kumulált relatív gyakoriságok diagram egy kicsit korábban. A diagram pontosan ugyanazokat az adatokat tartalmazza, amelyeket csak teszteltünk, így ezek az eredmények szépen konvergálnak.
kutatási kérdésünkkel kapcsolatban: úgy tűnik, hogy csak a 4.próba reakcióidejei oszlanak meg.

SPSS Kolmogorov-Smirnov teszt vizsgálja változók

egy alternatív módja annak, hogy fut a Kolmogorov-Szmirnov teszt indul elemezni leíró statisztikák Exploreas alább látható.

Kolmogorov-Szmirnov Teszt Szintaxis a Nemparaméteres Vizsgálatokat

Results

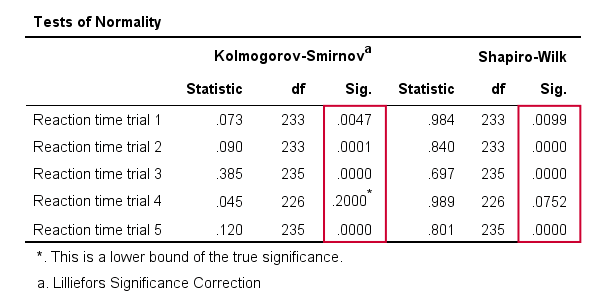
As a rule of thumb, we conclude thata variable is not normally distributed if “Sig.” < 0.05.Tehát mind a Kolmogorov-Smirnov teszt, mind a Shapiro-Wilk teszt eredményei azt sugallják, hogy csak a 4.reakcióidő-próba követi a normális eloszlást az egész populációban.
továbbá vegye figyelembe, hogy a Kolmogorov-Smirnov vizsgálati eredmények megegyeznek az NPAR tesztekből nyert eredményekkel.

Beszámolási egy Kolmogorov-Szmirnov Teszt

A jelentéstétel a vizsgálati eredmények alábbi APA iránymutatás, írunk valamit, mint”a Kolmogorov-Szmirnov teszt azt jelzi, hogy a reakció idők tárgyalása 1 nem követnek normális eloszlást, D(233) = 0.07, p = 0.005.”További változók, próbálja lerövidíteni, de győződjön meg róla, hogy include

• D (a “különbség”), a Kolmogorov-Szmirnov teszt statisztika,
• df, a szabadságfok (ami egyenlő N), valamint
• p, a statisztikai szignifikanciát.

rossz eredmények az SPSS-ben?

Ha egy diák, aki csak azt akarja, hogy adja át a tesztet, akkor hagyja abba az olvasást most. Csak kövesd az eddig megbeszélt lépéseket, és jó leszel.

jobb, most futtassuk újra ugyanazokat a teszteket az SPSS 18-as verziójában, majd nézzük meg a kimenetet.

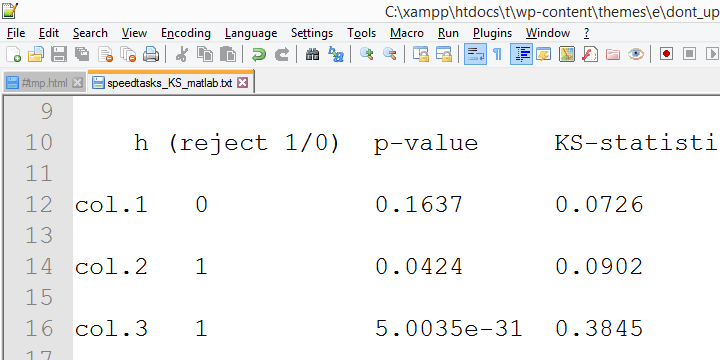
ebben a kimenetben a pontos p-értékek szerepelnek, és-szerencsére – nagyon közel vannak az aszimptotikus p-értékekhez. Kevésbé szerencsére, bár, az SPSS verzió 18 Az eredmények vadul különböznek
az SPSS verziótól 24 resultswe eddig jelentett.
az Ok úgy tűnik, hogy a Lilliefors szignifikancia korrekció, amelyet az újabb SPSS verziókban alkalmaznak. Az eredmény úgy tűnik, hogy az aszimptotikus szignifikancia szintek sokkal jobban különböznek a pontos jelentőségtől,mint akkor, amikor a korrekciót nem értjük. Ez komoly kétségeket vet fel a “Lilliefors eredmények” helyességével kapcsolatban-ez az alapértelmezett az újabb SPSS verziókban.
ennek a javaslatnak a konvergáló bizonyítékait kollégám, Alwin Stegeman gyűjtötte össze, aki a MATLAB összes tesztjét megismétli. A Matlab eredményei megegyeznek az SPSS 18 eredményeivel, ezért nem az újabb eredményekkel.

Kolmogorov – Smirnov normality teszt-Korlátozott hasznosság

a Kolmogorov – Smirnov teszt gyakran teszteli a sok statisztikai teszt, például az ANOVA, a t-teszt és még sok más által megkövetelt normalitás feltételezést. Azonban szinte rutinszerűen figyelmen kívül hagyják, hogy az ilyen vizsgálatok robusztusak e feltételezés megsértése ellen, ha a mintaméretek ésszerűek, mondjuk n ≥ 25.Ennek oka a központi limit tétel. Ezért a normalitási vizsgálatokra csak kis minta méretekre van szükségha a cél a normalitás feltételezésének kielégítése.
sajnos a kis mintaméretek alacsony statisztikai teljesítményt eredményeznek a normalitás tesztekhez. Ez azt jelenti, hogy a normalitástól való jelentős eltérések nem eredményeznek statisztikai jelentőséggel. A teszt szerint nincs eltérés a normalitástól, miközben valójában hatalmas. Röviden, Az a helyzet, amelyben normalitási tesztekre van szükség-kis mintaméretek – szintén az a helyzet, amelyben rosszul teljesítenek.

köszönöm az olvasást.