Articles

Fisica

by admin

Sappiamo dalla cinematica che l’accelerazione è un cambiamento di velocità, nella sua grandezza o nella sua direzione, o entrambi. Nel moto circolare uniforme, la direzione della velocità cambia costantemente, quindi c’è sempre un’accelerazione associata, anche se la grandezza della velocità potrebbe essere costante. Si verifica questa accelerazione da soli quando si gira un angolo in auto. (Se si tiene la ruota ferma durante una svolta e si muove a velocità costante, si è in movimento circolare uniforme.) Quello che noti è un’accelerazione laterale perché tu e l’auto state cambiando direzione. Più nitida è la curva e maggiore è la velocità, più evidente sarà questa accelerazione. In questa sezione esaminiamo la direzione e la grandezza di tale accelerazione.

La figura 1 mostra un oggetto che si muove in un percorso circolare a velocità costante. La direzione della velocità istantanea è mostrata in due punti lungo il percorso. L’accelerazione è nella direzione del cambiamento di velocità, che punta direttamente verso il centro di rotazione (il centro del percorso circolare). Questo puntamento è mostrato con il diagramma vettoriale nella figura. Chiamiamo l’accelerazione di un oggetto che si muove in un movimento circolare uniforme (risultante da una forza esterna netta) l’accelerazione centripeta(ac); centripeto significa “verso il centro” o “centro che cerca.”

La figura data mostra un cerchio, con un triangolo con vertici A B C fatti dal centro al limite. A è al centro e i punti B e C sono al percorso del cerchio. Le linee A B e A C agiscono come raggi e B C è un accordo. Delta theta è mostrato all'interno del triangolo, e la lunghezza dell'arco delta s e la lunghezza della corda delta r sono anche dati. Nel punto B, la velocità dell'oggetto è mostrata come v uno e nel punto C, la velocità dell'oggetto è mostrata come v due. Lungo il cerchio un'equazione è mostrata come delta v uguale a v sub 2 meno v sub 1.

Figura 1. Vengono mostrate le direzioni della velocità di un oggetto in due punti diversi e il cambiamento di velocità Δv è visto puntare direttamente verso il centro di curvatura. (Vedi piccolo riquadro.) Poiché ac = Δv / Δt, l’accelerazione è anche verso il centro; ac è chiamata accelerazione centripeta. (Poiché Δθ è molto piccolo, la lunghezza dell’arco Δs è uguale alla lunghezza della corda Δr per piccole differenze di tempo.)

La direzione dell’accelerazione centripeta è verso il centro di curvatura, ma qual è la sua grandezza? Si noti che il triangolo formato dai vettori di velocità e quello formato dai raggi r e Δs sono simili. Entrambi i triangoli ABC e PQR sono triangoli isosceli (due lati uguali). I due lati uguali del triangolo vettoriale della velocità sono le velocità v1 = v2 = v. Usando le proprietà di due triangoli simili, otteniamo \frac{\Delta{v}}{v}=\frac{\Delta{s}}{r}\\.

L’accelerazione è \frac{\Delta{v}}{\Delta{t}}\\, e quindi prima risolviamo questa espressione per Δv:

\displaystyle\Delta{v}=\frac{v}{r}\Delta{s}\\.

Quindi dividiamo questo per Δt, producendo

\displaystyle\frac{\Delta{v}}{\Delta{t}}=\frac{v}{r}\times\frac{\Delta{s}}{\Delta{t}}\\.

Infine, notare che \frac{\Delta{v}}{\Delta{t}}=a_c\\ e \frac{\Delta{s}}{\Delta{t}}=v\\, lineare o di velocità tangenziale, vediamo che l’entità dell’accelerazione centripeta è

{a}_c=\frac{v^2}{r}\\,

che è l’accelerazione di un oggetto in un cerchio di raggio r ad una velocità v. Quindi, l’accelerazione centripeta è maggiore alle alte velocità e in curve strette (raggio più piccolo), come hai notato quando guidi un’auto. Ma è un po ‘ sorprendente che ac sia proporzionale alla velocità al quadrato, il che implica, ad esempio, che è quattro volte più difficile prendere una curva a 100 km/h che a 50 km/h. Un angolo acuto ha un raggio piccolo, quindi ac è maggiore per curve più strette, come probabilmente avrete notato.

È anche utile esprimere ac in termini di velocità angolare. Sostituendo v = rw nell’espressione precedente, troviamo a_c = \ frac {\left (r\omega\right)^2}{r}=r\omega^2\\. Possiamo esprimere la grandezza dell’accelerazione centripeta usando una delle due equazioni:

\displaystyle{a}_c=\frac{v^2}{r}; a_c=r\omega^2\\.

Ricorda che la direzione di ac è verso il centro. È possibile utilizzare qualsiasi espressione sia più conveniente, come illustrato negli esempi seguenti.

Una centrifuga (vedi Figura 2b) è un dispositivo rotante utilizzato per separare campioni di densità diverse. L’elevata accelerazione centripeta riduce significativamente il tempo necessario per la separazione e rende possibile la separazione con piccoli campioni. Le centrifughe sono utilizzate in una varietà di applicazioni nella scienza e nella medicina, tra cui la separazione di sospensioni a cellule singole come batteri, virus e cellule del sangue da un mezzo liquido e la separazione di macromolecole, come DNA e proteine, da una soluzione. Le centrifughe sono spesso valutate in termini di accelerazione centripeta rispetto all’accelerazione dovuta alla gravità (g); l’accelerazione centripeta massima di diverse centinaia di migliaia di g è possibile nel vuoto. Centrifughe umane, centrifughe estremamente grandi, sono state utilizzate per testare la tolleranza degli astronauti agli effetti di accelerazioni più grandi di quelle della gravità terrestre.

Esempio 1. Come si confronta l’accelerazione centripeta di un’auto attorno a una curva con quella dovuta alla gravità?

Qual è l’entità dell’accelerazione centripeta di un’auto che segue una curva di raggio 500 m ad una velocità di 25,0 m/s (circa 90 km / h)? Confronta l’accelerazione con quella dovuta alla gravità per questa curva abbastanza delicata presa a velocità autostradale. Vedi Figura 2a.

Strategia

Poiché v e r sono dati, la prima espressione in \displaystyle{a}_c=\frac{v^2}{r}; a_c=r\omega^2\\ è la più comoda da usare.

Soluzione

Inserendo il dato valori di v = 25.0 m/s e r=500 m nella prima espressione per ac dà

\displaystyle{a}_c=\frac{v^2}{r}=\frac{\left(25.0\text{ m/s}\right)^2}{a 500\text{ m}}=1.25\text{ m/s}^2\\.

Discussione

Per confrontare questo con l’accelerazione dovuta alla gravità (g = 9,80 m/s2), prendiamo il rapporto di \displaystyle\frac{a_c}{g}=\frac{\left(1.25 \ text{ m / s}^2 \ right)} {\left (9.80 \ text{ m / s}^2 \ right)}=0.128\\. Pertanto, ac=0,128 g ed è evidente soprattutto se non si indossava una cintura di sicurezza.

Nella figura a, un'auto mostrata dall'alto corre su una strada circolare attorno a un percorso circolare. Il centro del parco è definito come il centro di questo cerchio e la distanza da questo punto alla macchina è preso come raggio r. La velocità lineare è mostrata in direzione perpendicolare verso la parte anteriore dell'auto, mostrata come v l'accelerazione centripeta è mostrata con una freccia puntata verso il centro di rotazione. Nella figura b, viene mostrata una centrifuga un oggetto di massa m ruota in esso a una velocità costante. L'oggetto è alla distanza uguale al raggio, r, della centrifuga. L'accelerazione centripeta è mostrata verso il centro di rotazione e la velocità, v è mostrata perpendicolare all'oggetto in senso orario.

Figura 2. (a) L’auto che segue un percorso circolare a velocità costante viene accelerata perpendicolarmente alla sua velocità, come mostrato. La grandezza di questa accelerazione centripeta si trova nell’esempio 1. b) Una particella di massa in una centrifuga ruota a velocità angolare costante . Deve essere accelerato perpendicolarmente alla sua velocità o continuerebbe in linea retta. L’entità dell’accelerazione necessaria si trova nell’esempio 2.

Esempio 2. Quanto è grande l’accelerazione centripeta in un Ultracentrifugo?

Calcola l’accelerazione centripeta di un punto 7.50 cm dall’asse di un ultracentrifugo che gira a 7,5 × 104 giri / min. Determina il rapporto tra questa accelerazione e quella dovuta alla gravità. Vedi Figura 2b.

Strategia

Il termine giri / min sta per giri al minuto. Convertendo questo in radianti al secondo, otteniamo la velocità angolare ω. Poiché r è dato, possiamo usare la seconda espressione nell’equazione a_c=\frac{v^2}{r};a_c=r\omega^2\\ per calcolare l’accelerazione centripeta.

Soluzione

Per convertire 7.50 × 104 giri/min in radianti al secondo, usiamo i fatti che una rivoluzione è 2π rad e un minuto è 60.0 s. Così,

\displaystyle\omega=7.50\times10^4\frac{\text{rev}}{\text{min}}\times\frac{2\pi\text{ rad}}{1\text{ ap}}\times\frac{1\text{ min}}{60.0\text{ s}}=7854\text{ rad/s}\\ .

Ora l’accelerazione centripeta è data dalla seconda espressione in

\displaystyle{a}_c=\frac{v^2}{r}; a_c=r\omega^2\\ as ac = rw2.

La conversione di 7,50 cm in metri e la sostituzione di valori noti danno ac = (0,0750 m) (7854 rad/s) 2 = 4.63 × 106 m / s2.

Si noti che i radianti senza unità vengono scartati per ottenere le unità corrette per l’accelerazione centripeta. Prendendo il rapporto tra ac e g si ottiene

\frac{a_c}{g}= \ frac {4.63 \ times10^6}{9.80}=4.72\times10^5\\.

Discussione

Quest’ultimo risultato significa che l’accelerazione centripeta è 472.000 volte più forte di g. Non c’è da meravigliarsi che tali centrifughe ω elevate siano chiamate ultracentrifughe. Le accelerazioni estremamente grandi coinvolte riducono notevolmente il tempo necessario per causare la sedimentazione delle cellule del sangue o di altri materiali.

Naturalmente, è necessaria una forza esterna netta per causare qualsiasi accelerazione, proprio come proposto da Newton nella sua seconda legge del moto. Quindi è necessaria una forza esterna netta per causare un’accelerazione centripeta. Nella Forza centripeta, considereremo le forze coinvolte nel movimento circolare.

Esplorazioni PhET: Ladybug Motion 2D

Scopri i vettori di posizione, velocità e accelerazione. Spostare la coccinella impostando la posizione, velocità o accelerazione, e vedere come i vettori cambiano. Scegli il movimento lineare, circolare o ellittico e registra e riproduci il movimento per analizzare il comportamento.

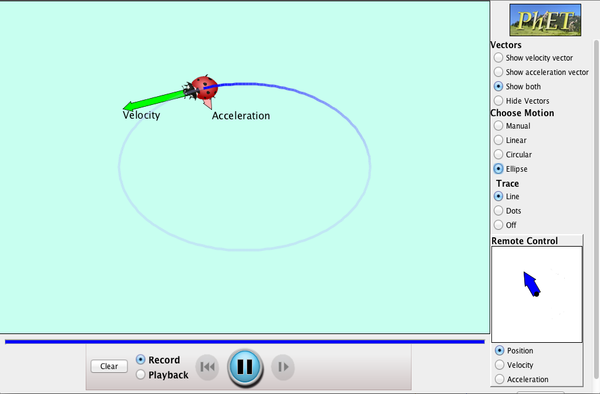
Schermata Coccinella Movimento 2D.

Fare clic sull’immagine per scaricare. Utilizzare Java per eseguire la simulazione.

Riepilogo della sezione

  • Accelerazione centripeta ac è l’accelerazione sperimentata durante un movimento circolare uniforme. Punta sempre verso il centro di rotazione. È perpendicolare alla velocità lineare v e ha la grandezza {a}_{\text{c}}=\frac{{v}^{2}} {r}; {a} _ {\text{c}}={\mathrm{r\omega}} ^{2}\\.
  • L’unità di accelerazione centripeta è m / s2.

Domande concettuali

  1. L’accelerazione centripeta può cambiare la velocità del movimento circolare? Spiegare.

Problemi& Esercizi

  1. Un giro in fiera fa girare i suoi occupanti all’interno di un contenitore a forma di disco volante. Se il percorso circolare orizzontale che i piloti seguono ha un raggio di 8,00 m, a quanti giri al minuto i piloti saranno sottoposti ad un’accelerazione centripeta la cui magnitudine è 1,50 volte quella dovuta alla gravità?
  2. Un corridore che partecipa alla corsa di 200 m deve correre intorno alla fine di una pista che ha un arco circolare con un raggio di curvatura di 30 m. Se completa la corsa di 200 m in 23,2 s e corre a velocità costante per tutta la gara, qual è l’entità della sua accelerazione centripeta mentre percorre la porzione curva della pista?
  3. Prendendo l’età della Terra per essere di circa 4 × 109 anni e assumendo il suo raggio orbitale di 1.5 × 1011 non è cambiato ed è circolare, calcolare la distanza totale approssimativa Terra ha viaggiato dalla sua nascita (in un quadro di riferimento stazionario rispetto al Sole).
  4. L’elica di un aereo da caccia della seconda guerra mondiale ha un diametro di 2,30 m. (a) Qual è la sua velocità angolare in radianti al secondo se gira a 1200 giri/min? (b) Qual è la velocità lineare della sua punta a questa velocità angolare se l’aereo è fermo sull’asfalto? (c) Qual è l’accelerazione centripeta della punta dell’elica in queste condizioni? Calcolalo in metri al secondo quadrato e convertilo in multipli di g.
  5. Una macina da officina ordinaria ha un raggio di 7,50 cm e ruota a 6500 giri / min. (a) Calcola la grandezza dell’accelerazione centripeta sul suo bordo in metri al secondo quadrato e convertila in multipli di g. (b) Qual è la velocità lineare di un punto sul suo bordo?
  6. Le lame dell’elicottero sopportano gli sforzi tremendi. Oltre a sostenere il peso di un elicottero, sono filate a velocità rapide e sperimentano grandi accelerazioni centripete, specialmente in punta. (a) Calcolare l’entità dell’accelerazione centripeta sulla punta di una lama di elicottero lunga 4,00 m che ruota a 300 giri/min. (b) Confrontare la velocità lineare della punta con la velocità del suono (presa per essere 340 m/s).
  7. I pattinatori olimpici sono in grado di girare a circa 5 giri/s. (a) Qual è la loro velocità angolare in radianti al secondo? (b) Qual è l’accelerazione centripeta del naso del pattinatore se si trova a 0,120 m dall’asse di rotazione? (c) Un pattinatore eccezionale di nome Dick Button è stato in grado di girare molto più velocemente negli 1950 di chiunque altro da allora—a circa 9 giri/s. Qual è stata l’accelerazione centripeta della punta del naso, supponendo che sia a 0,120 m di raggio? d) Commentare le grandezze delle accelerazioni rilevate. Si ritiene che Button abbia rotto piccoli vasi sanguigni durante i suoi giri.
  8. Quale percentuale dell’accelerazione sulla superficie terrestre è l’accelerazione dovuta alla gravità nella posizione di un satellite situato a 300 km sopra la Terra?
  9. Verificare che la velocità lineare di un ultracentrifugo è di circa 0,50 km/s, e la Terra nella sua orbita è di circa 30 km / s calcolando: (a) La velocità lineare di un punto su un ultracentrifugo 0.100 m dal suo centro, ruotando a 50.000 giri / min; (b) La velocità lineare della Terra nella sua orbita attorno al Sole (utilizzare i dati del testo sul raggio dell’orbita terrestre e approssimarlo come circolare).
  10. Si dice che una stazione spaziale rotante crei “gravità artificiale”—un termine vagamente definito usato per un’accelerazione che sarebbe rozzamente simile alla gravità. La parete esterna della stazione spaziale rotante sarebbe diventata un pavimento per gli astronauti, e l’accelerazione centripeta fornita dal pavimento avrebbe permesso agli astronauti di esercitare e mantenere la forza muscolare e ossea in modo più naturale rispetto agli ambienti spaziali non rotanti. Se la stazione spaziale ha un diametro di 200 m, quale velocità angolare produrrebbe una” gravità artificiale ” di 9,80 m/s2 sul bordo?
  11. Al decollo, un jet commerciale ha una velocità di 60,0 m/s. I suoi pneumatici hanno un diametro di 0,850 m. (a) A quanti giri / min ruotano i pneumatici? (b) Qual è l’accelerazione centripeta sul bordo del pneumatico? (c) Con quale forza deve un determinato batterio di 1,00 × 10-15 kg aggrapparsi al bordo? (d) Prendere il rapporto tra questa forza e il peso del batterio.
  12. Concetti integrati. I cavalieri in un parco di divertimenti a forma di nave vichinga appesa a un grande perno vengono ruotati avanti e indietro come un pendolo rigido. A volte vicino al centro della corsa, la nave è momentaneamente immobile nella parte superiore del suo arco circolare. La nave poi oscilla sotto l’influenza della gravità. (a) Supponendo un attrito trascurabile, trovare la velocità dei piloti nella parte inferiore del suo arco, dato che il centro di massa del sistema viaggia in un arco con un raggio di 14,0 m e i piloti sono vicini al centro di massa. (b) Qual è l’accelerazione centripeta nella parte inferiore dell’arco? (c) Disegnare un diagramma a corpo libero delle forze che agiscono su un cavaliere nella parte inferiore dell’arco. (d) Trovare la forza esercitata dalla corsa su un pilota di 60,0 kg e confrontarla con il suo peso. (e) Discutere se la risposta sembra ragionevole.
  13. Risultati irragionevoli. Una madre spinge il suo bambino su un’altalena in modo che la sua velocità sia 9.00 m / s nel punto più basso del suo percorso. L’altalena è sospesa 2,00 m sopra il centro di massa del bambino. (a) Qual è l’entità dell’accelerazione centripeta del bambino nel punto più basso? (b) Qual è l’entità della forza che il bambino esercita sul sedile se la sua massa è di 18,0 kg? (c) Cosa c’è di irragionevole in questi risultati? (d) Quali premesse sono irragionevoli o incoerenti?

Glossario

accelerazione centripeta: l’accelerazione di un oggetto che si muove in un cerchio, diretto verso il centro

ultracentrifugo: una centrifuga ottimizzata per la filatura di un rotore a velocità molto elevate

Soluzioni selezionate ai problemi& Esercizi

1. 12,9 giri / min

3. 4 × 1021 m

5. a) 3,47 × 104 m/s2, 3,55 × 103 g; b) 51,1 m/s

7. (a) 3,14 rad/s; (b) 118 m/s; (c) 384 m/s; (d)L’accelerazione centripeta avvertita dai pattinatori olimpici è 12 volte maggiore dell’accelerazione dovuta alla gravità. Questo è un bel po ‘ di accelerazione in sé. L’accelerazione centripeta avvertita dal naso di Button era 39,2 volte più grande dell’accelerazione dovuta alla gravità. Non c’è da meravigliarsi che abbia rotto piccoli vasi sanguigni nei suoi giri.

9. a) 0,524 km / s; b) 29,7 km/s

11. (a) 1,35 × 103 giri/min; (b) 8,47 × 103 m/s2; (c) 8,47 × 10-12 N; (d) 865

12. (a) 16,6 m/s; (b) 19,6 m/s2;

(c)

Un rettangolo con una base più lunga dell'altezza. Una linea verticale con punte di freccia su entrambe le estremità passa attraverso il rettangolo, bisezionando i lati orizzontali. La parte superiore della freccia è etichettata N e la parte inferiore è etichettata w. ;

(d) 1,76 × 103 N o 3,00 w, cioè la forza normale (verso l’alto) è tre volte il suo peso; (e) Questa risposta sembra ragionevole, dal momento che si sente costretta a salire sulla sedia MOLTO più forte della semplice gravità.

13. (a) 40,5 m/s2; (b) 905 N; (c) La forza nella parte (b) è molto grande. L’accelerazione in parte (a) è troppo, circa 4 g; (d) La velocità dell’oscillazione è troppo grande. Alla velocità data nella parte inferiore dell’oscillazione, c’è abbastanza energia cinetica per inviare il bambino fino in fondo, ignorando l’attrito.