L’articolo riportato di seguito fornisce una visione ravvicinata della funzione di produzione Cobb-Douglas.

La funzione di produzione Cobb-Douglas si basa sullo studio empirico dell’industria manifatturiera americana realizzato da Paul H. Douglas e C. W. Cobb. È una funzione di produzione omogenea lineare di grado uno che tiene conto di due input, lavoro e capitale, per l’intera produzione del .industria manifatturiera.

La funzione di produzione Cobb-Douglas è espressa come:

Q = ALa Cß

dove Q è l’output e L e С sono rispettivamente input di lavoro e capitale. A, a e β sono parametri positivi dove = a >O, β> O.

L’equazione dice che l’output dipende direttamente da L e C, e quella parte di output che non può essere spiegata da L e С è spiegata da A che è il ‘residuo’, spesso chiamato cambiamento tecnico.

La funzione di produzione risolto da Cobb-Douglas aveva 1/4 contributo del capitale per l’incremento dell’industria manifatturiera e 3/4 del lavoro, in modo che il C-D funzione di produzione è

Q = AL3/4 C1/4

che mostra i rendimenti di scala costanti, poiché il totale dei valori di L e С è uguale a uno: (3/4 + 1/4), vale a dire,(a + β = 1) . Il coefficiente di lavoratore nella funzione C-D misura l’aumento percentuale in (Q che deriverebbe da un aumento dell ‘ 1 per cento in L, mantenendo costante С.

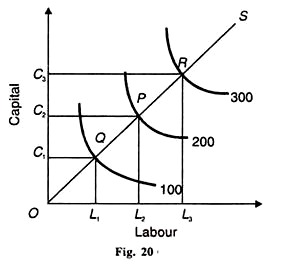
Allo stesso modo, В è l’aumento percentuale di Q che deriverebbe da un aumento dell ‘ 1% di C, mantenendo costante la L. La funzione di produzione C-D che mostra rendimenti costanti in scala è raffigurata nella Figura 20. L’input di lavoro è preso sull’asse orizzontale e il capitale sull’asse verticale.

Per produrre 100 unità di produzione, vengono utilizzate ОС, unità di capitale e OL unità di lavoro. Se la produzione dovesse essere raddoppiata a 200, gli input di lavoro e capitale dovrebbero essere raddoppiati. ОС è esattamente il doppio di ОС1 e di OL2 è il doppio di OL2.

Allo stesso modo, se la produzione deve essere aumentata di tre volte a 300, le unità di lavoro e capitale dovranno essere aumentate di tre volte. OC3 e OL3 sono tre volte più grandi di ОС1 e OL1, rispettivamente. Un altro metodo consiste nel prendere la linea di scala o il percorso di espansione che collega i punti di equilibrio Q, P e R. OS è la linea di scala o il percorso di espansione che unisce questi punti.

Mostra che gli isoquanti 100, 200 e 300 sono equidistanti. Quindi, sulla linea di scala OS OQ = QP = PR che mostra che quando il capitale e il lavoro sono aumentati in proporzioni uguali, anche la produzione aumenta nella stessa proporzione.

Critiche alla funzione di produzione CD:

La funzione di produzione CD è stata criticata da Arrow, Chenery, Minhas e Solow come discusso di seguito:

1. La funzione di produzione C-D considera solo due input, lavoro e capitale, e trascura alcuni input importanti, come le materie prime, che vengono utilizzate nella produzione. Non è quindi possibile generalizzare questa funzione su più di due input.

2. Nella funzione di produzione C-D, il problema della misurazione del capitale sorge perché richiede solo la quantità di capitale disponibile per la produzione. Ma il pieno utilizzo del capitale disponibile può essere fatto solo nei periodi di piena occupazione. Questo è irrealistico perché nessuna economia è sempre pienamente impiegata.

3. La funzione di produzione CD è criticata perché mostra ritorni costanti alla scala. Ma i ritorni costanti alla scala non sono una realtà, poiché i ritorni crescenti o decrescenti alla scala sono applicabili alla produzione.

Non è possibile modificare tutti gli input per apportare un cambiamento proporzionato ai risultati di tutti i settori. Alcuni input sono scarsi e non possono essere aumentati nella stessa proporzione degli input abbondanti. D’altra parte, input come macchine,imprenditorialità, ecc. sono indivisibili. Quando la produzione aumenta a causa dell’uso di fattori indivisibili alla loro capacità massima, il costo unitario diminuisce.

Quindi quando l’offerta di input è scarsa e sono presenti indivisibilità, non sono possibili ritorni costanti su scala. Ogni volta che le unità dei diversi input sono aumentate nel processo di produzione, le economie di scala e la specializzazione portano ad aumentare i ritorni su scala.

In pratica, tuttavia, nessun imprenditore vorrà aumentare le varie unità di input per avere un aumento proporzionato della produzione. Il suo sforzo è quello di avere un aumento più che proporzionato della produzione, anche se non sono esclusi rendimenti decrescenti su scala.

4. La funzione di produzione C-D si basa sull’assunzione di sostituibilità dei fattori e trascura la complementarità dei fattori.

5. Questa funzione si basa sul presupposto di una concorrenza perfetta nel mercato dei fattori che non è realistico. Se, tuttavia, questa ipotesi viene eliminata, i coefficienti α e β non rappresentano quote di fattore.

6. Uno dei punti deboli della funzione CD è il problema di aggregazione. Questo problema sorge quando questa funzione viene applicata a tutte le imprese di un settore e all’intero settore. In questa situazione, ci saranno molte funzioni di produzione di aggregazione bassa o alta. Quindi la funzione CD non misura ciò che mira a misurare.

Conclusione:

Quindi la praticabilità della funzione di produzione C-D nell’industria manifatturiera è una proposta dubbia. Questo non è applicabile all’agricoltura dove per la coltivazione intensiva, l’aumento delle quantità di fattori produttivi non aumenterà la produzione proporzionalmente. Anche allora, non si può negare che i ritorni costanti alla scala sono una tappa nella vita di un’impresa, di un’industria o di un’economia. È un’altra cosa che questa fase può venire dopo un po ‘ di tempo e per un breve periodo.

È Importante:

Nonostante queste critiche, la funzione CD è di grande importanza.

1. È stato ampiamente utilizzato negli studi empirici delle industrie manifatturiere e nei confronti interindustriali.

2. Viene utilizzato per determinare le quote relative di lavoro e capitale nella produzione totale.

3. È usato per dimostrare il teorema di Eulero.

4. I suoi parametri a e b rappresentano coefficienti di elasticità che vengono utilizzati per i confronti intersettoriali.

5. Questa funzione di produzione è lineare omogenea di grado uno che mostra rendimenti costanti in scala, Se α + β = 1, ci sono rendimenti crescenti in scala e se α + β < 1, ci sono rendimenti decrescenti in scala.

6. Gli economisti hanno esteso questa funzione di produzione a più di due variabili.