Articles

Notazione di Funzione e Come Valutare una Funzione

by admin

Il comune di notazione di una funzione è di solito scritto come,

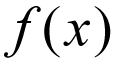
f(x) f è qualche espressione che coinvolge la variabile x

non ci pensano troppo alla lettera, f viene moltiplicato per x. Invece, considerare questo come una espressione matematica che viene letto come

f è una funzione di x

O

f è un'espressione che contiene la variabile o la lettera x

le Funzioni possono anche essere scritto in diversi modi, utilizzando altre variabili, ad esempio

  • g(x), h(x) e k(x)

In aggiunta, le funzioni possono prendere altri valori di input diverso da x.

  • f(a), h(r) e k(m)

L’idea chiave è sempre da ricordare che la variabile al di fuori della parentesi è il “nome” della funzione, mentre la variabile all’interno della parentesi è il valore di ingresso della funzione.

Ad esempio, la seguente è chiamata funzione k con un valore di input di m.

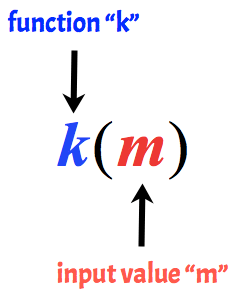
k(m) può essere letta come la funzione di k di m. ciò significa che la funzione k è espressa in termini di m poiché m è il valore di input.

Esempi di base di valutazione delle funzioni

Esempio 1: Valutare la funzione .

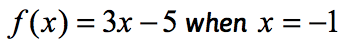
f(x) = 3x - 5 quando x=-1

Questa è la normale notazione di funzione in cui la funzione f, mentre il valore di input x. Valutare una funzione, quello che vogliamo è quello di sostituire ogni istanza di x nell’espressione e quindi semplificare.

Poiché x = – 1, sostituiamo questo valore nella funzione e semplifichiamo. In tal modo, otteniamo una soluzione simile a questa.

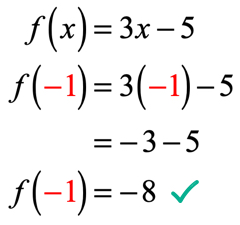
f(x) = 3x - 1 → f(-1) = 3(-1) - 5 → f (-1) = -3 -5 = -8. pertanto, f(-1) = -8.

Esempio 2: Valutare la funzione .

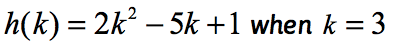
h(k) = 2k^2-5k+1 quando k=3

Osservare che la funzione qui è h e il valore di ingresso è k. Proprio come nel nostro esempio precedente, vogliamo sostituire qualunque sia il valore numerico assegnato a k nella funzione data e semplificare.

Poiché k = 3, la soluzione dovrebbe essere simile a questa

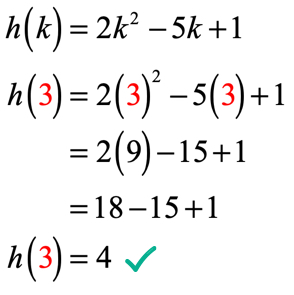
h (k) = 2k^2 - 5k + 1 → h(3) = 2(3)^2 - 5(3) + 1 → h(3) = 2(9) -15+1 → h(3) = 18 - 15 + 1 → h (3) = 4.

Esempio 3: Valutare ogni valore di x nella tabella sottostante utilizzando la funzione sottostante. Tracciare i punti nell’asse xy e collegare i punti per rivelare il grafico della funzione.

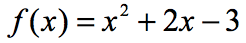
f(x) = x^2 + 2x - 3
una tabella di valori per la funzione f (x o f(x) dove i valori di x sono -4, -3, -2, -1, 0, 1 e 2

Dato che ci sono sette x-ingressi, il che significa che valuteremo la funzione di sette volte. Prova a lavorare questo fuori da soli poi tornare a controllare le risposte.

Se l’hai fatto correttamente, questi sono i valori:

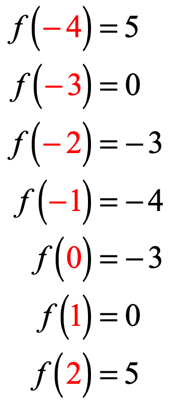
questi sono i valori della funzione quando valutati con ogni valore x o valore di input. f (-4) = 5, f(-3) = 0, f(-2)=-3, f(-1) = -4, f(0) = -3, f(1) = 0, f(2) = 5.

Ora possiamo inserire quei valori di output nella tabella.

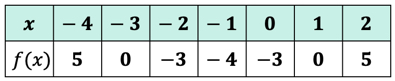
ecco la tabella completa dei valori rappresentati come un insieme di coppie ordinate: { (-4,5), (-3,0), (-2,-3), (-1,-4), (0,-3), (1,0), (2,5) }

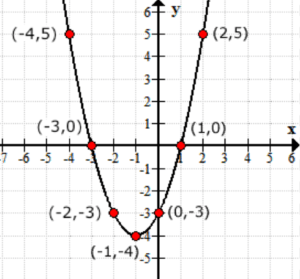
Pensa ai valori di output della funzione f\left( x \right) come ai valori y. Ecco come appare il grafico sull’asse xy.

dopo riportando i punti dalla tabella generata dalla funzione f(x) = x^2 + 2x -3 si ottiene una parabola, che si apre con un minimo di a (-1,-4), l'intercetta y -3 e x-intercetta di -3 e 1.

Esempi intermedi di valutazione delle funzioni

Esempio 4: Dato che g\left( x \right) = {x^2} – 3x + 1, trova g\left( {2x – 1} \right).

Negli esempi precedenti, abbiamo valutato una funzione per un numero. Questa volta il valore di input non è più un valore numerico fisso, ma invece un’espressione. Potrebbe sembrare complicato, ma la procedura rimane la stessa.

Sostituiremo ogni istanza di x in g\left( x \right) con il valore di input che è 2x – 1. Semplifica quadrando il binomio, applicando la proprietà distributiva e combinando termini simili.

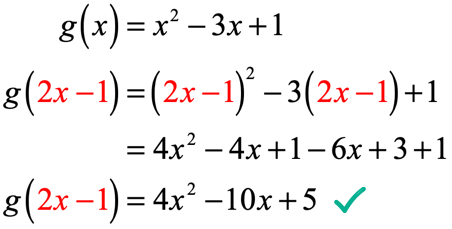
g(x)=x^2-3x+1 → g(2x-1) = (2x-1)^2 - 3(2x-1) +1 → g(2x-1) = 4x^2-4x+1-6x+3=1 → g(2x-1) = 4x^2 - 10x + 5

Esempio 5: Dato che p\left( x \right) = {{4x – 1} \over x} , valutare p\left( 1 \right) – p\left( { – 1} \right).

Il problema potrebbe sembrare intimidatorio all’inizio, ma una volta che lo analizziamo e applichiamo ciò che già sappiamo su come valutare le funzioni, questo non dovrebbe essere così male!

Quello che dobbiamo fare qui è valutare la funzione a x = 1 quindi sottrarre per il valore della funzione quando valutata a x = – \,1.

Fai molta attenzione quando sostituisci i valori e durante il processo di semplificazione. Se non stai attento in ogni passaggio, è molto facile commettere errori quando aggiungi, sottrai, moltiplica o dividi numeri positivi e negativi.

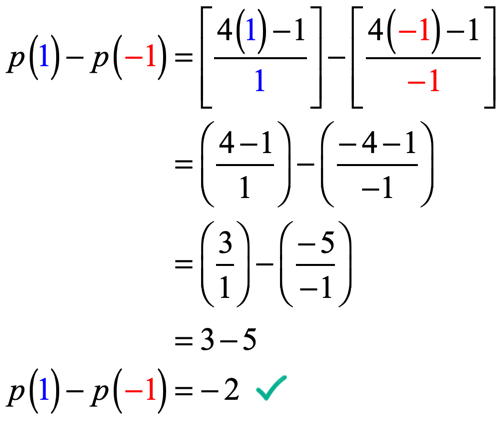
p(1) - p(-1) = { /(1) } - { /(-1) } = - = 3-5 → p(1) - p(-1) = -2

Avanzato Esempio di Applicazione del Concetto di Valutazione Funzioni

Esempio 6: Se f\left( 2 \right) = 9, trovare il valore di a in funzione qui sotto.

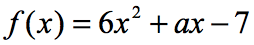
f(x) = 6x^2 + ax -7, trova il valore di un

Nell’equazione, f\left( 2 \right) = 9, ci viene detto che se l’input del la funzione è 2; l’uscita della funzione sarà 9. Poiché la funzione ci viene data, la nostra prima mossa è quella di sostituire almeno il valore di 2 e quindi semplificare. Questo è quello che otterremo.

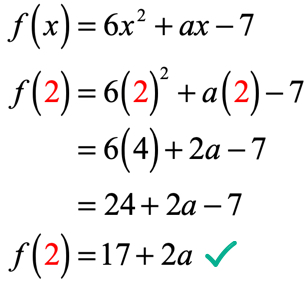
f(x) = 6x^2 + ax - 7 → f(2) = 6(2)^2 + a (2) - 7 → f(2) = 6(4) +2a - 7 = 24 + 2a - 7 → f(2) = 17 + 2a

L’output della funzione dopo aver valutato a x = 2 è 17 + 2a. Ricordate, ci viene anche detto che l’uscita è a 9 utilizzando il dato equazione f\left( 2 \right) = 9. Quindi quello che dobbiamo fare ora è pari a vicenda, e risolvere l’equazione lineare per il valore incognito di una.

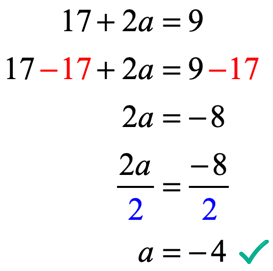
17 + 2a = 9 → 17-17+2a = 9-17 → 2a = -8 → (2a)/2 = -8/2 → a= -4

proviamo a verificare se il valore di a = – \,4 in f(x) = 6{x^2} + ax – 7 può rendere la condizione f\left( 2 \right) = 9 per essere una vera dichiarazione.

f(x) = 6x^2 - 4x -7 → f(2) = 6(2)^2 - 4(2) - 7 = 6(4) - 8- 7 = 24 - 8 - 7 → f(2) = 9

È vero! Quindi, abbiamo risolto con successo per il valore corretto di a.