Un tensore è un array di dati(numeri, funzioni, ecc.) che viene espanso in qualsiasi numero (0 e maggiore) di dimensioni. Il numero di dimensioni è chiamato rango di tensore.

Rango 0 tensore

Un tensore che non ha dimensioni (0).

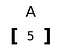
Rank 1 tensore

Un tensore che viene espanso in una sola dimensione.

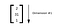
Rank 2 tensor

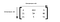
Rank 3 tensor

As shown in figure, a rank 3 tensor has a cube (or cuboid like structure).

If rank of a tensor exceeds 3, it becomes difficult to visualize.

Scalare

Uno scalare è un tensore di rango 0. In fisica, varie quantità sono rappresentate come uno scalare come: Distanza (500 km), Temperatura (10ºC), Velocità (34 km/h), ecc.

Vettore

Un tensore di rango 1 è chiamato vettore. Grandezze fisiche quali Velocità (10 m / s), Spostamento (54 m verso Est), Campo elettromagnetico (1 V/m).

Differenza tra scalare e vettore :

Una quantità che non richiede informazioni aggiuntive (come la direzione) con essa (come la temperatura) è rappresentata come scalare. Mentre, una quantità che ha bisogno di una direzione da specificare accanto alla sua grandezza è rappresentata con un vettore (come il campo elettrico).

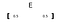
Un vettore è indicato in grassetto lettera (come la “E” ) o una freccia sopra la lettera.

Per tracciare un vettore usiamo i suoi elementi come valore delle coordinate (rispettivamente asse x, y e z). Qui, il primo elemento (0.5) è preso come valore x e il secondo elemento (anche, 0.5) è preso come valore y (se avessimo tre elementi, il terzo sarebbe stato il valore z).

Dopo aver tracciato il vettore come punto abbiamo messo una freccia ad esso, dal punto di origine(0,0).

Un vettore è semplicemente una matrice che ha una riga (chiamata vettore colonna) o una colonna (chiamata vettore riga).

Matrice

Una matrice è un tensore di rango 2. Abbiamo esaminato matrix in precedenza.

Un tensore con rango maggiore di 2 viene semplicemente chiamato “tensore” (non esiste un nome specifico per tensori con rango maggiore di 2).

Il concetto di tensore generalizza le matrici, i vettori e gli scalari sotto lo stesso tetto (sono tutti tensori ma con ranghi diversi).

Matrici come prodotto di vettori:

Quando due vettori vengono moltiplicati formano una matrice.

Vector X and Y combined, have 6 elements but their product alone has 9 elements. Pertanto, alcune matrici potrebbero essere scomposte come prodotto di due vettori.