Un test di normalità alternativa è il test Shapiro-Wilk.

• Che cos’è un test di normalità di Kolmogorov-Smirnov?
• SPSS Kolmogorov-Smirnov test da TEST NPAR
• SPSS Kolmogorov-Smirnov test da ESAMINARE VARIABILI
• Segnalazione di un test Kolmogorov-Smirnov
• Risultati errati in SPSS?

Che cos’è un test di normalità Kolmogorov-Smirnov?

Il test Kolmogorov-Smirnov esamina se è probabile che i punteggi seguano una certa distribuzione in alcune popolazioni.Per evitare confusione, ci sono 2 test Kolmogorov-Smirnov:

• c’è un campione di test Kolmogorov-Smirnov per testare se una variabile segue una data distribuzione in una popolazione. Questa ” distribuzione data “è di solito-non sempre – la distribuzione normale, quindi”test di normalità di Kolmogorov-Smirnov”.
• c’è anche il (molto meno comune) campioni indipendenti Kolmogorov-Smirnov test per testare se una variabile ha distribuzioni identiche in 2 popolazioni.

In teoria, “test Kolmogorov-Smirnov” potrebbe riferirsi a entrambi i test (ma di solito si riferisce al test Kolmogorov-Smirnov di un campione) e sarebbe meglio evitarlo. A proposito, entrambi i test Kolmogorov-Smirnov sono presenti in SPSS.

Kolmogorov-Smirnov Test – Semplice esempio

Quindi diciamo che ho una popolazione di 1.000.000 di persone. Penso che i loro tempi di reazione su qualche compito siano perfettamente distribuiti normalmente. Provo 233 di queste persone e misuro i loro tempi di reazione.
Ora la distribuzione di frequenza osservata di questi probabilmente differirà un po ‘ – ma non troppo – da una distribuzione normale. Quindi eseguo un istogramma sui tempi di reazione osservati e sovrappongo una distribuzione normale con la stessa media e deviazione standard. Il risultato è mostrato di seguito.

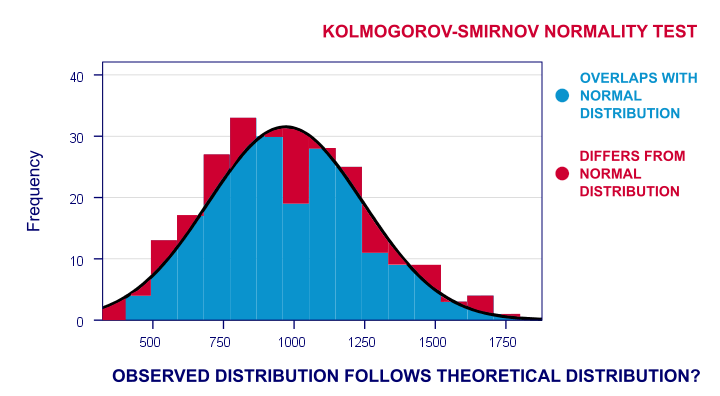
La distribuzione di frequenza dei miei punteggi non si sovrappone completamente alla mia curva normale. Ora, potrei calcolare la percentuale di casi che si discostano dalla curva normale-la percentuale di aree rosse nel grafico. Questa percentuale è una statistica di test: esprime in un singolo numero quanto i miei dati differiscono dalla mia ipotesi nulla. Quindi indica in che misura i punteggi osservati si discostano da una distribuzione normale.
Ora, se la mia ipotesi nulla è vera, allora questa percentuale di deviazione dovrebbe probabilmente essere piuttosto piccola. Cioè, una piccola deviazione ha un valore di probabilità alto o un valore P.
Al contrario, un’enorme percentuale di deviazione è molto improbabile e suggerisce che i miei tempi di reazione non seguono una distribuzione normale nell’intera popolazione. Quindi una grande deviazione ha un valore p basso. Come regola generale, wereject l’ipotesi nulla se p < 0.05.So se p < 0.05, non crediamo che la nostra variabile segua una distribuzione normale nella nostra popolazione.

Kolmogorov-Smirnov Test – Test statistico

Quindi questo è il modo più semplice per capire come funziona il test di normalità di Kolmogorov-Smirnov. Computazionalmente, tuttavia, funziona in modo diverso: confronta le frequenze relative cumulative osservate rispetto alle attese come mostrato di seguito.

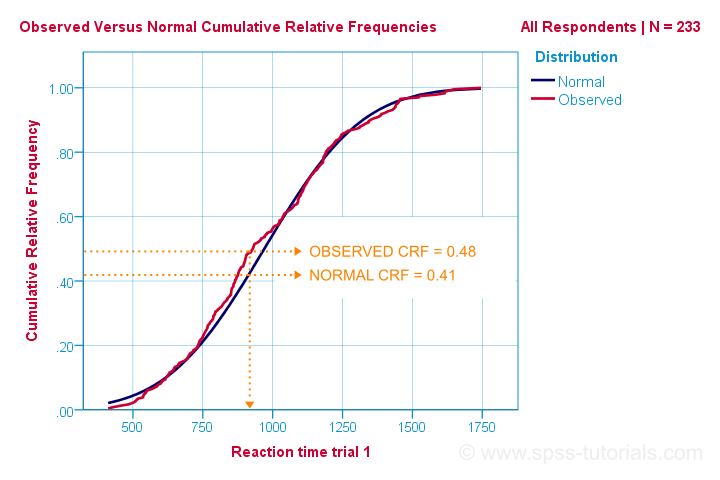
Il test di Kolmogorov-Smirnov utilizza la differenza assoluta massima tra queste curve come statistica del test indicata con D. In questo grafico, la differenza assoluta massima D è (0,48 – 0,41 =) 0,07 e si verifica in un tempo di reazione di 960 millisecondi. Tieni presente che D = 0.07 come lo incontreremo nel nostro output SPSS in un minuto.

Il test Kolmogorov-Smirnov in SPSS

Ci sono 2 modi per eseguire il test in SPSS:

• TEST NPAR come si trova sotto Analizza Test non parametrici Legacy Dialogs 1-Sample K-S… è il nostro metodo di scelta perché crea un output ben dettagliato.
• ESAMINARE LE VARIABILI da Analizzare Statistiche descrittive Explore è un’alternativa. Questo comando esegue sia il test Kolmogorov-Smirnov che il test di normalità Shapiro-Wilk.
  Si noti che EXAMINE VARIABLES utilizza l’esclusione listwise dei valori mancanti per impostazione predefinita. Quindi, se testo5 variabili, i miei 5 test utilizzano solo casi che non hanno mancanze su nessuna di queste 5 variabili. Questo di solito non è quello che vuoi, ma mostreremo come evitarlo.

Dimostreremo entrambi i metodi usando speedtasks.sav in tutto, parte dei quali è mostrato di seguito.

La nostra principale domanda di ricerca èquale delle variabili del tempo di reazione è probabile che sia normalmente distribuita nella nostra popolazione?Questi dati sono un esempio da manuale del motivo per cui dovresti ispezionare accuratamente i tuoi dati prima di iniziare a modificarli o analizzarli. Facciamo proprio questo ed eseguiamo alcuni istogrammi dalla sintassi sottostante.

Risultato

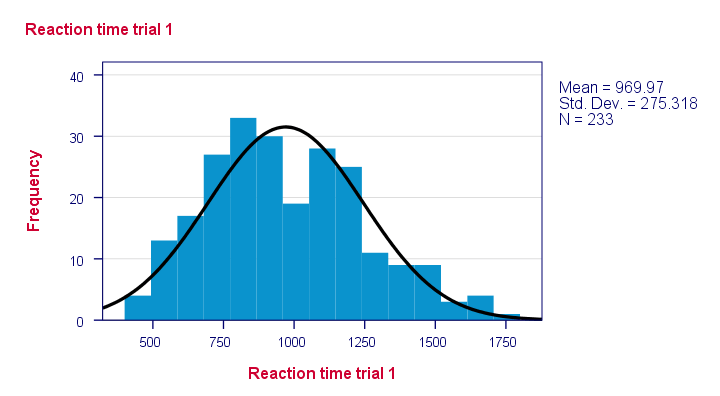
Si noti che alcune distribuzioni non sembrano affatto plausibili. Ma quali sono probabilmente distribuiti normalmente?

SPSS Kolmogorov-Smirnov test da TEST NPAR

La nostra opzione preferita per l’esecuzione del test Kolmogorov-Smirnov è underAnalyze Test non parametrici Legacy Dialogs 1-Esempio K-S… come mostrato di seguito.

Successivamente, compiliamo la finestra di dialogo come mostrato di seguito.

Facendo clic su Incolla si ottiene la sintassi seguente. Facciamolo.

Kolmogorov-Smirnov Test Sintassi da test non parametrici

Risultati

Prima di tutto, nota che la statistica del test per la nostra prima variabile è 0.073-proprio come abbiamo visto nel nostro grafico delle frequenze relative cumulative un po ‘ prima. Il grafico contiene esattamente gli stessi dati su cui abbiamo appena eseguito il nostro test, quindi questi risultati convergono bene.
Per quanto riguarda la nostra domanda di ricerca: solo i tempi di reazione per la prova 4 sembrano essere normalmente distribuiti.

SPSS Kolmogorov-Smirnov test da EXAMINE VARIABLES

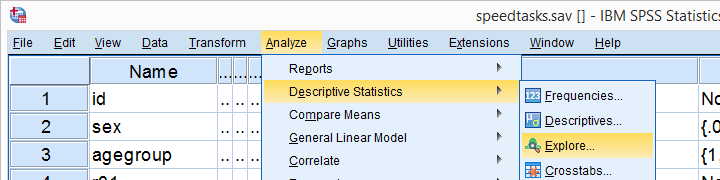
Un modo alternativo per eseguire il test Kolmogorov-Smirnov inizia da Analyze Descriptive Statistics Exploreas mostrato di seguito.

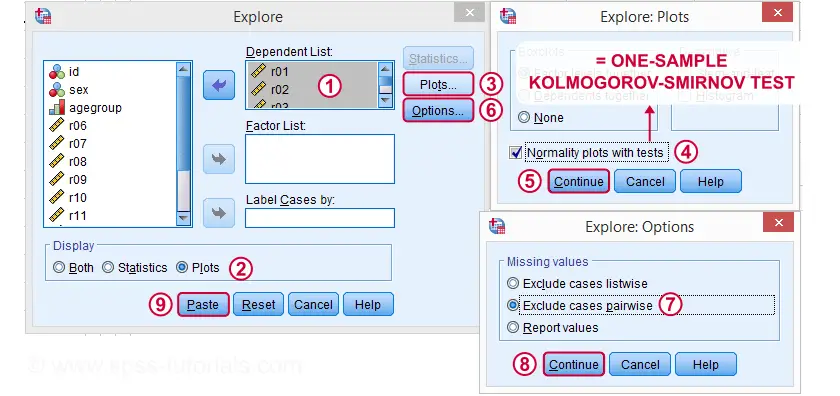
Kolmogorov-Smirnov Test Sintassi da test non parametrici

Results

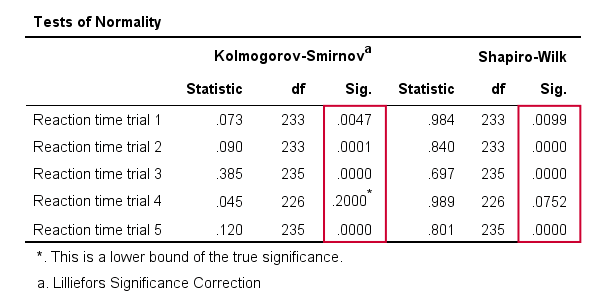
As a rule of thumb, we conclude thata variable is not normally distributed if “Sig.” < 0.05.Quindi sia il test Kolmogorov-Smirnov che i risultati del test Shapiro-Wilk suggeriscono che solo la prova a tempo di reazione 4 segue una distribuzione normale nell’intera popolazione.
Inoltre, si noti che i risultati del test Kolmogorov-Smirnov sono identici a quelli ottenuti dai TEST NPAR.

Segnalazione di un test di Kolmogorov-Smirnov

Per riportare i risultati del test seguendo le linee guida APA, scriveremo qualcosa come”un test di Kolmogorov-Smirnov indica che i tempi di reazione nel trial 1 non seguono una distribuzione normale, D(233) = 0,07, p = 0,005.”Per ulteriori variabili, prova ad accorciarlo ma assicurati di includere

• D (per “differenza”), la statistica del test Kolmogorov-Smirnov,
• df, i gradi di libertà (che è uguale a N) e
• p, la significatività statistica.

Risultati errati in SPSS?

Se sei uno studente che vuole solo superare un test, puoi smettere di leggere ora. Basta seguire i passaggi di cui abbiamo discusso finora e sarai bravo.

Giusto, ora eseguiamo di nuovo gli stessi test in SPSS versione 18 e diamo un’occhiata all’output.

In questo output sono inclusi i valori p esatti e-fortunatamente-sono molto vicini ai valori p asintotici. Meno fortunatamente,però, i risultati della versione 18 di SPSS sono molto diversi
dai risultati della versione 24 di SPSS abbiamo riportato finora.
La ragione sembra essere la correzione del significato di Lilliefors che viene applicata nelle versioni SPSS più recenti. Il risultato sembra essere che i livelli di significatività asintotica differiscono molto di più dal significato esatto rispetto a quando la correzione non è implicita. Ciò solleva seri dubbi sulla correttezza dei” Risultati Lilliefors ” – l’impostazione predefinita nelle versioni SPSS più recenti.
Convergenti prove per questo suggerimento è stato raccolto dal mio collega Alwin Stegeman che reran tutti i test in Matlab. I risultati Matlab concordano con i risultati SPSS 18 e-quindi-non con i risultati più recenti.

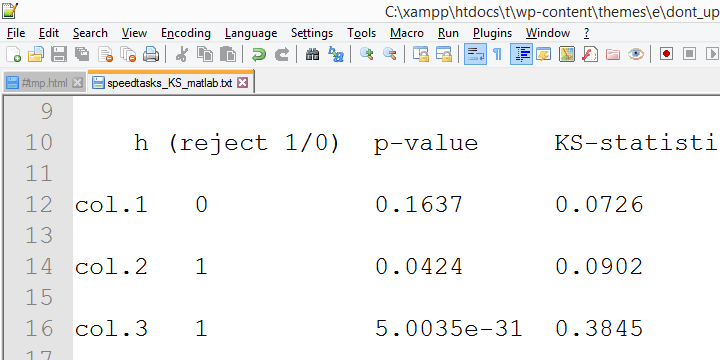
Kolmogorov – Smirnov normality test-Utilità limitata

Il test Kolmogorov – Smirnov è spesso quello di testare l’ipotesi di normalità richiesta da molti test statistici come ANOVA, il t-test e molti altri. Tuttavia, è quasi di routine trascurato che tali test sono robusti contro una violazione di questa ipotesi se le dimensioni del campione sono ragionevoli, ad esempio N ≥ 25.La ragione di fondo di questo è il teorema del limite centrale. Pertanto, i test di normalità sono necessari solo per campioni di piccole dimensioni, se l’obiettivo è quello di soddisfare l’ipotesi di normalità.
Sfortunatamente, piccole dimensioni del campione comportano una bassa potenza statistica per i test di normalità. Ciò significa che deviazioni sostanziali dalla normalità non comporteranno significatività statistica. Il test dice che non c’è deviazione dalla normalità mentre è in realtà enorme. In breve, la situazione in cui sono necessari test di normalità-piccole dimensioni del campione – è anche la situazione in cui funzionano male.

Grazie per la lettura.