信頼性に関して言えば、並列は、並列構造の要素のいずれかがシステムを機能させるこ これは、並列のコンデンサが回路内で特定の動作を提供し、1つのコンデンサが故障した場合、システムが故障する可能性があるため、物理的に並列
この単純な図では、並列にn個のコンポーネントがあり、システムが機能するためにはいずれかのコンポーネントが必要です。

コンポーネント#2が失敗した場合、他のコンポーネントはシステムの機能を許可します。

シンプルです。 そして、非常に便利です。 この構造は個々の部品の信頼性の上で全面的な信頼性の改善を、可能にする。 最も弱い部品が信頼性を限るシリーズシステムとは違って、ここに重複を加えることによってシステム信頼性は改善する。

二つのコンポーネント並列システムを考えてみましょう。 両方のコンポーネントが両方とも機能している場合、システムは機能しています。 コンポーネント1または2のいずれかに障害が発生した場合でも、システムは動作しています。 両方のコンポーネントが失敗した場合にのみ、システムは失敗します。 1つの障害でシステム障害が発生する直列システムとは異なり、この単純な例では、システム障害の前に2つの障害イベントが発生する必要があり

二つの失敗を持つ可能性は何ですか？ この式は、構成要素1または構成要素2が動作する確率に基づいています。 導出を行わずに、2つのコンポーネント並列システムの信頼性を次のように書くことができます。

これは、3つ以上のコンポーネ 並列システムを計算する別の方法を検討する前に、最初に言及する特別なケースの状況があります。並列のコンポーネントが同じ場合（信頼性に関して）、上記は単純化されます

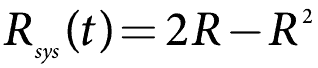
多くの場合、信頼性の低い、または1–R(t)を使用して並列システム計算を行う方が簡単です。 これはCDFまたはF（t）でもあります。 数学は今、一つの補正を持つシリーズシステムのようなものです。 一般的なケースでは、並列システムのシステム信頼性式は次のようになります。

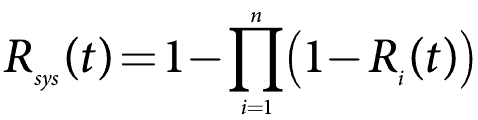
だから、1年間の使用で信頼性を持つ5つのコンポーネント、R(1)、90%、または0.9があるとしましょう。 システムの信頼性を計算します。上記の式を使用し、各要素の信頼性を0.9に設定すると、

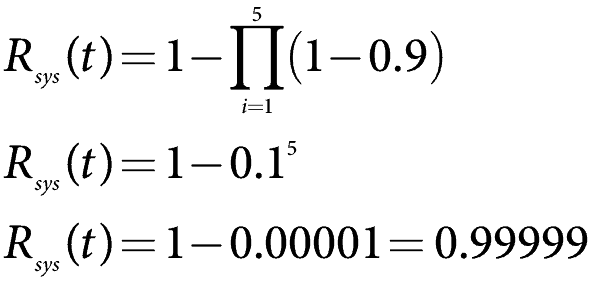
非常に信頼性があります。

冗長部品をシステムに追加するのは高価ですが、場合によっては、信頼性要件を満たすシステムを作成するのが適切なソリ もちろん、実際のシステムには、単にコンポーネントを並列に設定するだけでは、多くのバリエーションと複雑さがあります。 負荷分散、ホット、ウォーム、コールドスタンバイ、スイッチングまたは投票システム、および他の多くは、並列システムの構築を複雑にする可能性があります。

コンポーネントを並列に使用することは、個々のコンポーネントの信頼性の限界を超えてシステムの信頼性を高める唯一の方法です。

信頼性ブロック図の概要と値（記事）

信頼性割当（記事）

k out of n（記事）