収益は、会社がもたらすお金の量です。 この場合、収益は、購読あたりの価格に購読者の数または数量を掛けることによって見つけることができます。 私たちは、私たちに方程式\text{Revenue}=pQを与える、サブスクリプションごとの価格と数量のためのQのための変数、pを導入することができます。

加入者の数は価格によって変化するため、変数間の関係を見つける必要があります。 現在、p=30、Q=84,000であることがわかります。 また、価格が32ドルに上昇すると、新聞は5,000人の加入者を失い、2番目の値のペア、p=32とQ=79,000を与えることも知っています。 このことから、2つの量に関連する線形方程式を見つけることができます。 傾きは次のようになります

\begin{align}m&=\dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{-5,000}{2}\\&=-2,500\end{align}

これは、紙が価格を上げるごとに2,500人の加入者を失うことを示しています。 その後、y切片を解くことができます。

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.\テキスト{収益}=pQ\\テキスト{収益}=p\左（-2,500p+159,000\右）\\テキスト{収益}=p\左（-2,500p+159,000\右）\\テキスト{収益}=p\左（-2,500p+159,000\右）\\テキスト{収益}=p\左（-2,500p+159,000\右）\\テキスト{収益}=p\左（-2,500p+159,000\右）\\テキスト{収益}=p\左（-2,500p+159,000\右）\\テキスト{収益}=p\左（-2,500p+159,000\右）\\テキスト{収益}=p\左（-2,500p+159,000\右）\\テキスト{収益}=p\”>\text{revenue}=-2,500{p}^{2}+159,000p\end{align}

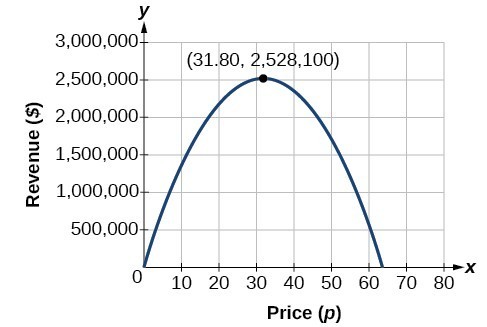
サブスクリプション料金の関数として、収益の二次関数が得られました。 新聞の収益を最大化する価格を見つけるために、頂点を見つけることができます。\begin{align}h&=-\dfrac{159,000}{2\left（-2,500\right）}\\&=31。8\end{align}

このモデルは、新聞が購読のために3 31.80を請求する場合、最大収益が発生することを示しています。 最大収益が何であるかを見つけるために、収益関数を評価します。=-2,500{\左（31.8\右）}^{2}+159,000\左（31.8\右）\\&=$2,528,100\hfill\end{align}

解の分析

これは二次式をグラフ化することによっても解決できます。 二次関数のグラフで最大収益を見ることができます。p>