Articles

関数表記法と関数の評価方法

by admin

関数の一般的な表記法は、通常、

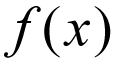
f(x)は、fが変数xを含む式であることを意味します

これも考えないでください文字通り、つまり、fはXに乗算されています。 代わりに、これを次のように読み取られる数式と考えてください

fはxの関数です

または

fは、変数または文字xを含む式です

関数は、

  • g(x),hさらに、関数は次を取ることができます。k（x）、およびk（x）

さらに、関数は次のようになります x以外の他の入力値。

  • f(a)、h(r)、およびk(m)

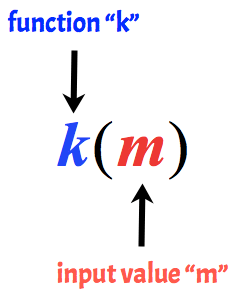
重要なアイデアは、括弧の外側の変数は関数の”名前”であり、括弧の内側の変数は関数の入力値であることを常に覚えておくことです。たとえば、以下はmの入力値を持つ関数kと呼ばれます。

k(m)はmのkの関数として読み取ることができます。 これは、mが入力値であるため、関数kがmで表されることを意味します。

関数を評価する基本的な例

例1：関数を評価します。

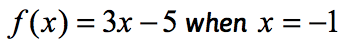
f(x)=3x-5when x=-1

これは、入力値がxである間に関数がfである関数の通常の表記法です。単純化する。

x=-1なので、この値を関数に代入して単純化します。 そうすることで、次のような解決策が得られます。p>

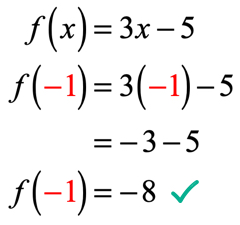
f(x)=3x-1→f(-1) = 3(-1) - 5 → f(-1)=-3-5=-8. したがって、f(-1)=-8です。

例2:関数を評価します。p>

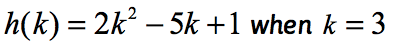
h(k)=2k^2-5k+1when k=3

ここでの関数はhであり、入力値はkであることに注意してください。 前の例のように、kに割り当てられた数値を与えられた関数に代入し、単純化したいと思います。k=3なので、解は次のようになります。

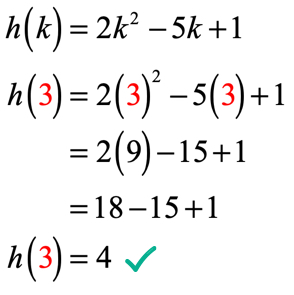
h（k）=2k^2-5k+1→h(3) = 2(3)^2 - 5(3) + 1 → h(3) = 2(9) -15+1 → h(3) = 18 - 15 + 1 → h(3)=4.

例3:以下の関数を使用して、以下の表のxの各値を評価します。 Xy軸の点をプロットし、点を接続して関数のグラフを表示します。

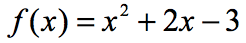
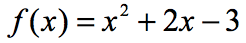
f（x）=x^2+2x-3

f（x）=x^2+2x-3
xまたはf(x)の関数fの値のテーブル。xの値は次のとおりです-4, -3, -2, -1, 0, 1 そして2

七つのx入力があるので、それは我々が同様に関数を七回評価することを意味します。 あなた自身でこれを試してみて、あなたの答えを確認するために戻ってきてください。あなたがそれを正しく行っているならば、これらは値です。

あなたがそれを正しく行っているならば、これらは値です。:p>

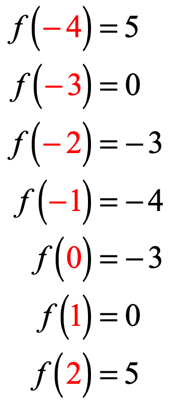
これらは、各x値または入力値で評価されたときの関数の値です。 f（-4）=5、f（-3）=0、f（-2）=-3、f（-1）=-4、f（0）=-3、f（1）=0、f（2）=5。

これらの出力値をテーブルに配置できるようになりました。p>

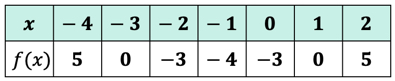
順序付けられたペアのセットとして表される値の完全なテーブルは次のとおりです: { (-4,5), (-3,0), (-2,-3), (-1,-4), (0,-3), (1,0), (2,5) }

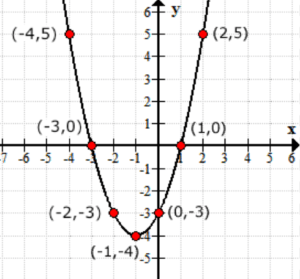
関数f\left(x\right)の出力値をy値と考えてください。 これは、グラフがxy軸上でどのように見えるかです。p>

関数f(x)=x^2+2x-3によって生成されたテーブルから点をプロットした後、（-1、-4）、y切片-3、x切片-3の最小値で開く放物線が得られます。-3と1。例4：g\left（x\right）={x^2}-3x+1とすると、g\left（{2x-1}\right）を見つける。

前の例では、数値で関数を評価してきました。 今回は、入力値が固定された数値ではなく、式になりました。 それは複雑に見えるかもしれませんが、手順は同じままです。g\left（x\right）のxのすべてのインスタンスを2x-1の入力値に置き換えます。 二項式を二乗し、分配特性を適用し、同様の項を組み合わせることによって単純化する。x^2-3x+1→g（2x-1）=（2x-1）^2-3（2x-1）+1→g（2x-1）=4x^2-4x+1

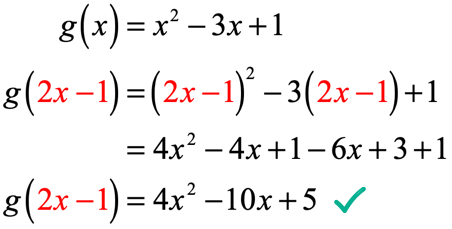
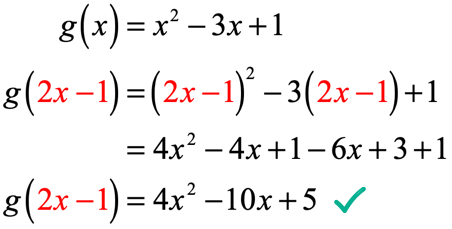
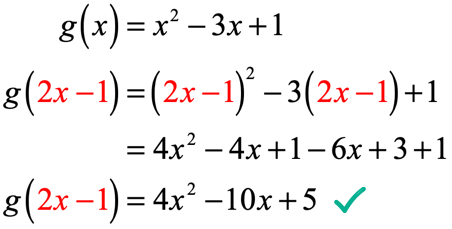
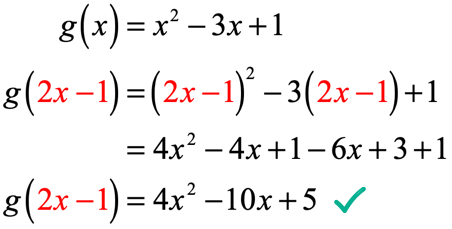g（x）=x^2-3x+1→g（2x-1）=（2x-1）^2-3（2x-1）+1→g（2x-1）=4x^2-4x+1g(x)=x^2-3x+1 → g(2x-1) = (2x-1)^2 - 3(2x-1) +1 → g(2x-1) = 4x^2-4x+1-6x+3=1 → g(2x-1) = 4x^2 - 10x + 5g(x)=x^2-3x+1 → g(2x-1) = (2x-1)^2 - 3(2x-1) +1 → g(2x-1) = 4x^2-4x+1-6x+3=1 → g(2x-1) = 4x^2 - 10x + 5g(x)=x^2-3x+1 → g(2x-1) = (2x-1)^2 - 3(2x-1) +1 → g(2x-1) = 4x^2-4x+1-6x+3=1 → g(2x-1) = 4x^2 - 10x + 5iv id=”447b3a9例5：p\left（x\right）={{4x-1}\over x}とすると、p\left（1\right）-p\left（{-1}\right）を評価します。問題は最初は威圧的に見えるかもしれませんが、それを分析して関数を評価する方法についてすでに知っていることを適用すると、これはそれほど悪ここで行う必要があるのは、x=1で関数を評価し、x=-\、1で評価されたときに関数の値で減算することです。値を代入するとき、および単純化プロセス中には非常に注意してください。

値を代入するとき、および単純化プロセス中には非常に注意してく あなたがすべてのステップで注意していない場合は、加算、減算、乗算、または正と負の数を分割するときに間違いを犯すことは非常に簡単です。p(1)-p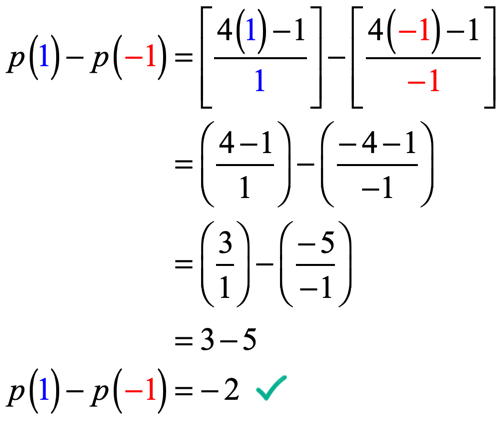p(1)-p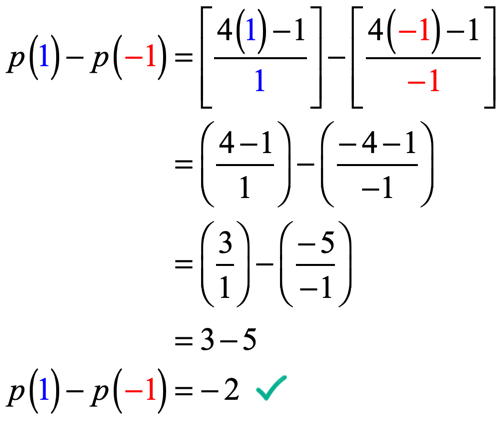p(1)-pp(1)-pp(1)-pp(1)-p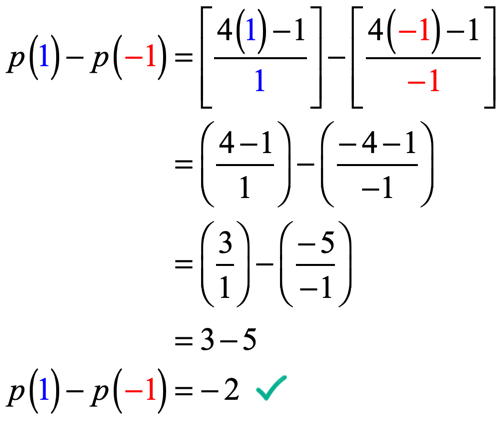p(1)-piv id=”(-1) = { /(1) } – { /(-1) } = – = 3-5 → p(1)-p(-1)=-2

関数を評価する概念を適用する高度な例

例6：f\left(2\right)=9の場合、以下の関数でaの値を見つけます。f（x）=6x^2+ax-7、aの値を見つける

式では、f\left（2\right）=9、関数の入力が2であれば、関数の入力が2であれば、関数の入力が2であれば、関数の入力が2であれば、関数の入力が2であれば、関数の入力が2であれば、; 関数の出力は9になります。 関数は私たちに与えられているので、私たちの最初の動きは、少なくとも2の値を代入してから単純化することです。 これが私たちが得るものです。f(x)=6x^2+ax-7→f(x)=6x^2+ax-7→f(x)=6x^2+ax-7→f(x)=6x^2+ax-7→f(x)=6x^2+ax-7→f(x)=6x^2+ax-7→f(x)=6x^2+ax-7→f(x)=6x^2+ax-7→f(x)=6x^2+ax-7→f(x)=6x^2+ax-7→f(x)=6x^2+ax-7→f(x)=6x^2+ax-7(2) = 6(2)^2 + a(2)-7→f(2)=6(4)+2a-7=24+2a-7→f(2)=17+2a

x=2で評価した後の関数の出力は17+2aです。f\left(2\right)=9を使用して出力が9であるとも言われています。 したがって、ここで行う必要があるのは、それらを互いに等しく設定し、aの未知の値の線形方程式を解くことです。

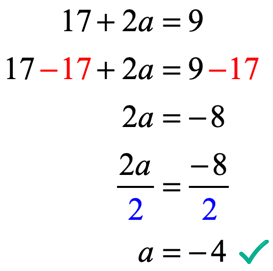
17+2a=9→17-17+2a=9-17→2a=-8→(2a)/2=-8/2→a=-4

f(x)=6{x^2}+ax-7のa=-\,4の値が与えられた条件f\left(2\right)=9を真の文にすることができるかどうかを確認しましょう。f(x)=6x^2-4x-7→f(x)=6x^2-4x-7→f(x)=6x^2-4x-7→f(x)=6x^2-4x-7→f(x)=6x^2-4x-7→f(x)=6x^2-4x-7→f(x)=6x^2-4x-7→f(x)=6x^2-4x-7→f(x)=6x^2-4x-7→f(x)=6x^2-4x-7→f(x)=6x^2-4x-7→f(x)(2) = 6(2)^2 – 4(2) – 7 = 6(4) – 8- 7 = 24 – 8 – 7 → f(2)=9

それは本当です！ したがって、我々は正常にaの正しい値のために解決しました。