Articles

Abstract data structures

by admin

Abstract data types

計算機科学では、抽象データ型(ADT)はデータ型の数学的モデルであり、データ型はデータのユーザーの観点からその動作(セマンティクス)によって定義され、データ型はデータ型の数学的モデルである。具体的には、可能な値、このタイプのデータに対する可能な操作、およびこれらの操作の動作について説明します。 これは、データの具体的な表現であり、ユーザーではなく実装者の視点であるデータ構造とは対照的です。正式には、ADTは「論理的な振る舞いが値の集合と演算の集合によって定義されるオブジェクトのクラス」として定義されることがあります。 「行動」の意味は作者によって異なり、行動の正式な仕様の2つの主なタイプは公理的（代数的）仕様と抽象モデルです; これらはそれぞれ抽象機械の公理的意味論と操作的意味論に対応する。 いくつかの著者はまた、（計算操作のための）時間と（値を表現するための）空間の両方の点で、計算の複雑さ（「コスト」）を含む。

抽象構造体を使用する理由は、それらに格納されているデータの設計に基づいてメモリを効率的に使用するためです。 非常に大量のデータまたは非常に頻繁にデータを変更すると、データ構造は、コンピュータプログラムの効率（実行時間）に大きな違いを生むことができます。 より一般的な言語では、抽象的なデータ構造は、整然とした配置に組み込まれたデータのほんの一部の配置です。

完全に素敵な概要

抽象データ構造のいくつかのタイプ

IBによって評価

  1. 静的および動的データ構造
  1. 配列
  2. 二次元配列
  3. スタック
  4. キュー
  5. リンクリスト
  6. ツリー
  7. バイナリツリー
  8. 二次元配列
  9. スタック
  10. キュー
  11. リンクリスト
  12. ツリー
  13. バイナリツリー
  14. 二次元配列
  15. 二次元配列
  16. スタック
  17. キュー
  18. リンクリスト
  19. ツリー
  20. バイナリツリー
  21. バイナリツリー
  22. コレクション
  23. 再帰

ibによって評価されていませんが、それらを知っている必要があります

  1. リスト
  2. 辞書
  3. セット
  4. タプル

データ構造の基本操作

私はsimon allardiceからこの優れたスライドを見つけました。 p>

配列の基本的な操作。png

異なるデータ構造の比較

データ構造 強み 弱点
配列 要素の挿入と削除、コレクショ>ソートと検索、挿入と削除-特に、配列の先頭または末尾に挿入と削除を行う場合
リンクリスト 直接インデックス作成、作成と使用が簡単 直接アクセス、検索とソート
スタックとキュー LIFO/FIFO用に設計された 直接アクセス、検索、ソート
バイナリツリー 挿入と削除の速度、アクセスの速度、ソート順を維持 いくつかのオーバーヘッド

ul>

  • 固定構造は高速/小型です
  • 抽象データ構造を使用する必要があるかどうかを検討しているときは、最も多くのデータを保持し、最も頻繁に変更されたデータを保持するものは何かを自問する必要があります。

    • 静的データ構造と動的データ構造の比較

    この比較は、コンピュータサイエンスの教科書から使用されています。

    静的データ構造 動的データ構造
    メモリが割り当てられているため、必要ではない可能性があります。 メモリの量が必要に応じて変化するので効率的です。
    プログラムの書き込み時にメモリ位置が固定されているため、データの各要素への高速アクセス。 実行時にメモリ位置が割り当てられるため、各要素へのアクセスが遅くなります。
    割り当てられたメモリアドレスは連続しているため、アクセスが速くなります。 割り当てられたメモリアドレスは、アクセスが遅く断片化される可能性があります。
    構造体は固定サイズであり、作業をより予測可能にします。 たとえば、ヘッダーを含めることができます。 構造体のサイズが異なるため、現在の構造体のサイズを知るためのメカニズムが必要です。
    データの異なる要素間の関係は変更されません。 データの異なる要素間の関係は、プログラムが実行されるにつれて変化します。

    使用するデータ構造の選択

    このグラフィックは、ダートフォード-グラマー-スクール-コンピュータ-サイエンス部門から多大な感謝を込めて使用されています。

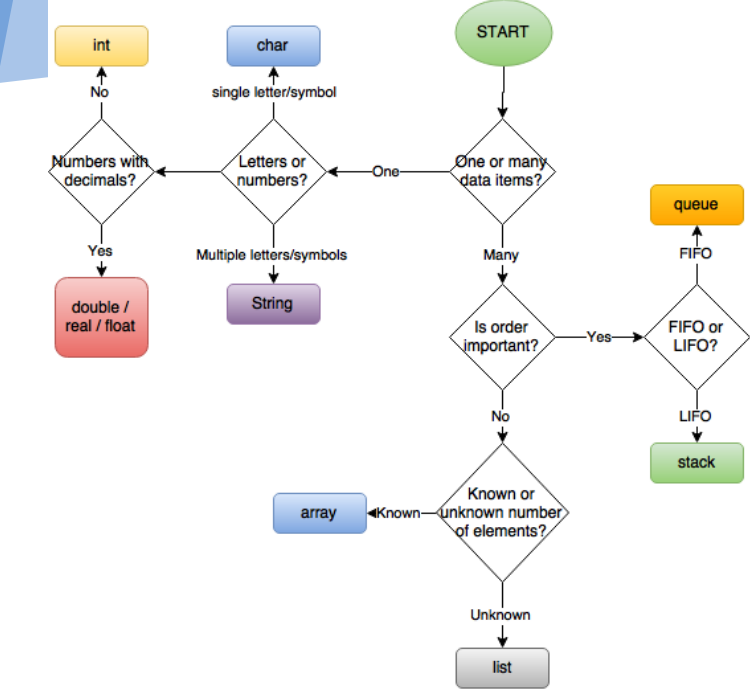
    データ型のフローチャートを選択します。png

    標準

    • 再帰的思考の使用を必要とする状況を特定します。
    • 指定された問題解決策で再帰的思考を識別します。
    • 再帰アルゴリズムをトレースして、問題の解を表現します。
    • 二次元配列の特性を記述します。
    • 二次元配列を使用してアルゴリズムを構築します。
    • スタックの特性とアプリケーションについて説明します。
    • スタックのアクセスメソッドを使用してアルゴリズムを構築します。
    • キューの特性とアプリケーションを説明します。
    • キューのアクセスメソッドを使用してアルゴリズムを構築します。
    • 静的スタックおよびキューとしての配列の使用について説明します。
    • 動的データ構造の特徴と特性を説明します。
    • リンクリストが論理的にどのように動作するかを説明します。
    • リンクされたリストをスケッチ（シングル、ダブル、円形）。
    • コレクションの特性と用途を説明します。
    • コレクションのアクセスメソッドを使用してアルゴリズムを構築します。
    • プログラムされたソリューション内のサブプログラムとコレクションの必要性を議論します。
    • 定義済みのサブプログラム、一次元配列、および/またはコレクションを使用してアルゴリズムを構築します。
    • ツリーが論理的にどのように動作するかを説明します(バイナリと非バイナリの両方)。
    • 用語を定義します: 親、左子、右子、サブツリー、ルートとリーフ。
    • inorder、postorder、preorderツリーのトラバーサルの結果を示します。
    • 二分木をスケッチします。
    • 動的データ構造という用語を定義します。
    • 静的データ構造と動的データ構造の使用を比較します。
    • 与えられた状況に適した構造を提案します。