수익 금액을 회사에 제공합니다. 이 경우 수익은 가입 횟수 당 가격에 가입자 수 또는 수량을 곱하여 찾을 수 있습니다. 구독 당 가격에 대한 p 와 수량에 대한 Q 라는 변수를 도입하여 방정식\text{수익}=pQ 를 제공 할 수 있습니다.

구독자 수가 가격에 따라 변하기 때문에 변수 간의 관계를 찾아야합니다. 우리는 현재 p=30 과 Q=84,000 을 알고 있습니다. 우리는 또한 가격이 32 달러로 상승하면 신문이 5,000 명의 가입자를 잃어 두 번째 값 쌍인 p=32 및 Q=79,000 을 제공한다는 것을 알고 있습니다. 이것으로부터 우리는 두 양과 관련된 선형 방정식을 찾을 수 있습니다. 경사가 될 것입니다.

\을 시작{맞춤}m&=\dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{-5,000}{2}\\&=-2,500\끝{맞춤}

이것은 우리에게 알려줍니다 종이 잃을 것이 2,500 명의 가입자를 각각 달러 그들은 높은 가격. 그런 다음 y-절편을 해결할 수 있습니다.

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.

&\text{수익}=pQ\\&\text{수익}=p\left(-2,500p+159,000\오른쪽)\\&\text{수익}=-2,500{p}^{2}+159,000p\끝{맞춤}

우리는 지금 이차 기능에 대한 수익의 기능으로 가입니다. 신문에 대한 수익을 극대화 할 가격을 찾으려면 정점을 찾을 수 있습니다.

\begin{align}h&=-\dfrac{159,000}{2\left(-2,500\right)}\\&=31.8\end{align}

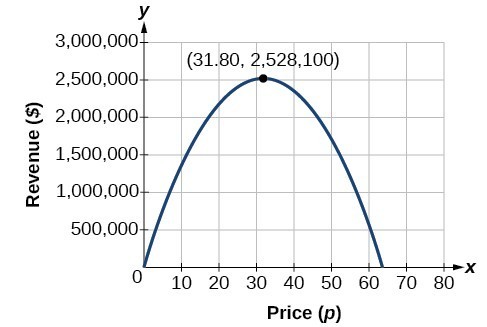
이 모델은 신문이 구독에 대해 31.80 달러를 청구하면 최대 수익이 발생한다고 알려줍니다. 최대 수익이 무엇인지 찾기 위해 수익 기능을 평가합니다.

\을 시작{맞춤}\text{최대 수익}&=-2,500{\left(31.8\오른쪽)}^{2}+159,000\left(31.8\오른쪽)\\&=\$2,528,100\hfill\끝{맞춤}

의 분석 솔루션

이것은 또한 수에 의해 해결 그래픽은 차입니다. 2 차 함수의 그래프에서 최대 수익을 볼 수 있습니다.